Published online by Cambridge University Press: 11 August 2014
For the past few years, stimulating research has been carried out on ordered statistics. Linear combinations of the sample ordered values are used to provide estimates of parameters of the population from which the sample is drawn. Such statistics are termed systematic by Mosteller. They are in common use, because they provide simple solutions of parametric problems of statistical estimation. Often they are inefficient, but this drawback is sometimes more than offset by the ease with which the calculations are performed.
Mosteller drew attention to the possible use of the statistics Wr , which he called quasi-range of rth order and defined as
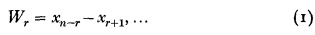
where x 1, x 2,…, x n are ordered observations in a sample of n from a population f(x) (x 1 < x 2 < … < xn ). The distributions of quasiranges in samples drawn from a normal population have been studied by Godwin and Cadwell.