No CrossRef data available.
Published online by Cambridge University Press: 11 August 2014
The simplest form of nomogram is a graphical device for representing a functional relationship between three variables in a manner which is often more convenient for practical reference than that of plotting a series of contours for chosen values of one of the three variables on a Cartesian graph. We develop the basis of such a nomogram by means of analytical geometry in this section.
The condition that three points (ξ1, η1), (ξ2, η2) and (ξ3, η3) shall be collinear is commonly expressed by means of the determinant
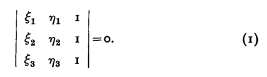
If the relationship between three variables a, b and c which we wish to represent nomographically is
F (a,b,c) = o, (2)
and we can express (2) in the determinantal form [similar to (1)]
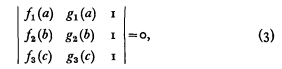
where f1f2 (a), f2 (b), f3 (c), g1 (a), g2 (b) and g3 (c) represent (generally) different functions of a, b and c, it is apparent that we can associate
any three particular values of a, b and c satisfying (2) with the points
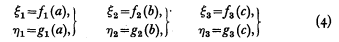
on a Cartesian graph; and they will be collinear because (3) is of the same form as (1).