Sheppard's correction to the variance

Extract

The variance of a continuous frequency distribution is often calculated by concentrating the frequencies in intervals of width h at the mid-points (vide Kendall, Advanced Theory of Statistics, Vol. 1, §3.16). Under certain conditions this approximation can be corrected by subtracting 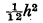from the calculated variance. This note gives an interpretation in elementary terms of the ‘reason’ for such a correction.

We consider three distributions, all having the same frequency in any one of the intervals of width h (Fig. 1):

C the original continuous distribution;

H where the frequency density is uniform within any one interval;

P where the frequency in an interval is concentrated at the mid-point.