No CrossRef data available.
Published online by Cambridge University Press: 11 August 2014
It has been said that everybody believes in the Law of Errors (i.e. the Normal distribution), the experimenters because they think it is a mathematical theorem and the mathematicians because they think it is an experimental fact. Text-books on statistics often seem to produce the Normal distribution as the conjurer produces a rabbit from a hat and the actuarial student, who should be something of both mathematician and experimenter, is frequently somewhat mystified as to why such an apparently complicated distribution function as
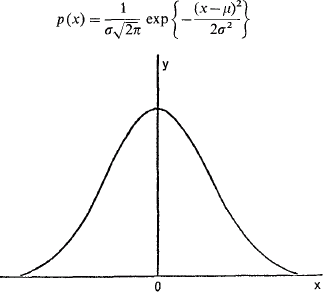
Fig. 1. The Normal distribution
(see Fig. 1) is suddenly introduced and given such prominence.