1 Introduction
1.1 Two (or more) heads are better than one
Ecologists have observed that cognitively simple animals (e.g., ants) are collectively capable of complex behaviour (e.g., nest building) and can solve problems that are intractable for individuals (Krause, Ruxton, & Krause, Reference Krause, Ruxton and Krause2010), an ability often referred to as collective intelligence. Likewise, human groups, when properly managed, tend to outperform the average (and frequently the best) individual, both in terms of the quality and quantity of solutions in a wide range of tasks, including judgement and prediction, creative thinking, concept attainment and brainstorming (Burgman, Reference Burgman2015; Cooke, Mendel & Thijs, Reference Cooke, Mendel and Thijs1988; Hanea, McBride, Burgman & Wintle, Reference Hanea, McBride, Burgman and Wintle2018; Hemming, Burgman, Hanea, McBride & Wintle, Reference Hemming, Burgman, Hanea, McBride and Wintle2017; Hill, Reference Hill1982; Lyle, Reference Lyle2008; Tetlock, Mellers, Rohrbaugh & Chen, Reference Tetlock, Mellers, Rohrbaugh and Chen2014; Woolley, Aggarwal & Malone, Reference Woolley, Aggarwal and Malone2015). The concept of collective intelligence is of course not new. In fact, democratic societies are founded upon the idea that groups produce superior solutions and make more accurate judgments because the collective has access to greater problem-solving resources (Aristotle, Trans. Reference Jowett and Barnes1984), especially if its members use effective processes for eliciting and aggregating information, beliefs and preferences (Hastie & Kameda, Reference Hastie and Kameda2005). Galton’s (Reference Galton1907) work is often heralded as the first rigorous demonstration of this “wisdom of the crowd” effect. He describes how a large group of pundits at a country fair guessed the dressed weight of an ox, and found their aggregated estimates fell within 1% of the true value. The effect is based on the statistical property that the random errors of a set of many diverse, independent judgments cancel out to reveal the underlying informational component (Surowiecki, Reference Surowiecki2005). Despite the fact that many real-world contexts tend to violate (at least some of) the basic assumptions underlying the wisdom of the crowd effect, evidence of its effective application have accumulated, e.g., in diagnostic radiological screening (Kämmer, Hautz, Herzog, Kunina-Habenicht & Kurvers, Reference Kämmer, Hautz, Herzog, Kunina-Habenicht and Kurvers2017; Kurvers et al., Reference Kurvers, Herzog, Hertwig, Krause, Carney, Bogart and Wolf2016; Wolf, Krause, Carney, Bogart & Kurvers, Reference Wolf, Krause, Carney, Bogart and Kurvers2015), geopolitical forecasts (Tetlock et al., Reference Tetlock, Mellers, Rohrbaugh and Chen2014), and weather and climate change predictions (Hueffer, Fonseca, Leiserowitz & Taylor, Reference Hueffer, Fonseca, Leiserowitz and Taylor2013; Sanders, Reference Sanders1963). Crowd wisdom may emerge despite violations of independence. For instance, Davis-Stober et al.’s (Reference Davis-Stober, Budescu, Dana and Broomell2014) empirically derived simulations demonstrated that aggregate judgments improve when individual estimates are negatively correlated, suggesting that divergent opinions can actually enhance collective judgment.
1.2 Crowdsourcing as a platform for harnessing collective intelligence
Crowdsourcing uses the unprecedented capacity to connect people over the internet to tap into the wisdom of the masses. Typical crowdsourcing platforms such as Amazon’s Mechanical Turk (AMT) involve the fragmentation of a larger task into so-called micro-tasks which are then completed in parallel by a large number of workers for a small fee, paid by the requester. The evidence suggests that crowdsourced solutions can increase performance and cost-effectiveness, although this depends to some extent on appropriate management of the platform, its users and the specific task design (Greengard, Reference Greengard2011). One of the key challenges is the fact that workers’ efforts cannot be assessed or controlled directly which may jeopardise the ultimate quality of the crowdsourced product. To manage this issue, requesters typically obtain multiple responses for each micro-task and aggregate contributions made by different workers. While aggregation is expected to improve the quality of the crowdsourced solution, obtaining multiple responses comes at greater cost for the requester. To maximise return on investment, it will be essential to understand how this built-in redundancy can be traded-off against the potential gain in overall product quality. In other words, how big should the crowd be to benefit maximally from their collective intelligence?
The question of what constitutes the optimal group size is not a new one. Condorcet’s jury theorem (Marquis De Condorcet, 1785) addresses the relative probability of a given group of individuals making a correct decision. Assuming the decision is made by majority vote, the theorem states that the optimal number of voters in the group depends on voters’ independent probability “p” of making the correct or incorrect decision. More precisely, if p > .5 (each voter is more likely to be correct than incorrect), increasing the group size also increases the probability that the majority vote will be correct. The classic study by Hogarth (Reference Hogarth1978) demonstrated that judgment accuracy increases as a function of group size, at least under specific constraints on judgement intercorrelation. Limited gains were achieved with groups exceeding 8–12 members. More recently, Galesic, Barkoczi and Katsikopoulos (Reference Galesic, Barkoczi and Katsikopoulos2018) examined the performance of groups under more realistic conditions, and at various task difficulty levels. They found that moderately sized groups may provide the greatest benefit, due to a loss on accuracy associated with large groups executing difficult tasks, which was larger than the corresponding increase in accuracy for easy tasks.
To our knowledge, the only study that has addressed the extent to which collective intelligence grows as a function of group size specifically in a crowdsourcing setting was conducted by Kosinski et al. (Reference Kosinski, Bachrach, Kasneci, Van Gael and Graepel2012). They crowdsourced multiple answers to items from the Raven’s Standard Progressive Matrices, a non-verbal intelligence test based on abstract reasoning. Using majority vote, they then sampled and aggregated n=1 to n=24 individual contributions for each test item to derive an overall test score that was subsequently converted to a standardised IQ score. This metric of “collective intelligence” was found to increase with the size of the group, showing the same diminishing returns described by Hogarth (Reference Hogarth1978). Most strikingly, the collective IQ based on just 12 individuals exceeded that of 99% of individuals within the general population, suggesting that crowdsourcing has the potential to substantially amplify human intelligence.
Our study aimed to replicate this study and test whether (a) the impressive result stands with a larger base sample, and (b) whether the estimated collective IQ based on crowdsourced answers exceeds the individual IQ of the contributing workers. In the Kosinski et al. (Reference Kosinski, Bachrach, Kasneci, Van Gael and Graepel2012) study, sample size effects were based on resampling a relatively limited set of responses across several experimental conditions, which included manipulations of worker characteristics and reward levels. We set out to replicate the key finding, using a simplified design to focus on the group size effect. We sampled unique responses from a much larger number of individual workers for each test item. By comparing the performance of groups varying in size against published normative data, we are able to test what percentage of the general population could be outperformed by a truly random sample of individual workers.
Another study examined group and individual performance based on traditional (not crowdsourced) administration of the Raven’s Standard Progressive Matrices (Bachrach, Graepel, Kasneci, Kosinski & Gael, Reference Bachrach, Graepel, Kasneci, Kosinski and Gael2012), and found that response aggregation resulted in a collective IQ that exceeded the best performing individual within the group. Our crowdsourced sample also included a subset of workers who completed the entire test, thus additionally allowing a direct comparison between collective IQ of a randomly assembled crowd, and the individual IQ of its constituent members.
2 Methods
2.1 Intelligence test
Raven’s Standard Progressive Matrices (RSPM) is one of the most commonly used intelligence tests across age groups. The RSPM consists of 60 multiple choice questions, which are – under normal test conditions – administered in order of increasing difficulty. The test measures reasoning ability, or more specifically, the deductive (“meaning-making”) component of general intelligence (Raven, Reference Raven2000). The standard form of the RSPM is composed of 5 sets (A-E) of 12 matrices, increasing in difficulty. In its intended form, an individual test-taker completes all 60 items and their raw score (number of correct items out of 60) is then compared against an age-matched norm group to derive an estimate of their IQ based on the score percentile. For instance, an 18-year old who answers 56 items correctly will be in the 75th percentile for her age group, which is equivalent to an IQ of 110.
2.2 Crowdsourcing procedures
As in Kosinski et al’s (Reference Kosinski, Bachrach, Kasneci, Van Gael and Graepel2012) study, we used Amazon’s Mechanical Turk (AMT; http://www.mturk.com) to crowdsource answers to the intelligence test. In the decade or so since its inception, the AMT user base has grown substantially, and the platform is also increasingly used to recruit participants for psychological research (Buhrmester, Kwang & Gosling, Reference Buhrmester, Kwang and Gosling2011; Buhrmester, Talaifar & Gosling, Reference Buhrmester, Talaifar and Gosling2018). For this study, we limited potential participants to AMT Masters, i.e., regular workers who have demonstrated excellence across a wide range of tasks and have continuously passed AMT’s statistical monitoring to maintain their qualification. The demographic profile of AMT workers has changed over the last few years, with increasing numbers of contributions from India, but the vast majority of workers are US-based (Difallah, Filatova & Ipeirotis, Reference Difallah, Filatova and Ipeirotis2018). For our purposes, the RSPM was divided into its constituent items and these were individually submitted to AMT as “Human Intelligence Tasks” (HITs), AMT’s generic term for the micro-tasks posted by requesters. We requested up to 200 responses per HITFootnote 1, and set a $0.05 payment and a maximum response time of 2 minutes for each. To further dissuade dishonest submissions, instructions were phrased so that workers recognised their reputation could suffer if they were found to be freeriding, although malicious or dishonest responses cannot be discounted. Workers could only complete each HIT once, but were not restricted from completing the other HITs in the full item set. To minimise bias related to weekly or daily fluctuations in AMT efficiency, all the HITs were published at the same time, in August 2017.
2.3 Group size and IQ calculation
For each HIT, we took a random sample (without replacement) of the responses, varying the sample size to create virtual groups of n=1 through to n=24. Within groups, responses were aggregated using the mode (or the “relative majority vote”). In the case of a tie, a random selection was made from the tied responses. Each group’s overall test score was calculated as the number of correct items (out of a total of 60 items/HITs). The raw score was then converted into a full-scale IQ score using the norms for adults as described in the RSPM manual (Raven, Reference Raven2000). We used the US-based norms, because the majority of MTurkers are from the US (Difallah et al., Reference Difallah, Filatova and Ipeirotis2018).
We then assessed the subset of participants (n=50) who each submitted all 60 possible HITs, thus completing the entire RSPM. This allowed us to calculate both individual IQs for these participants and the collective IQ of groups made up of randomly selected individuals from this sample. This procedure provides a more direct assessment of intellectual gain due to aggregation, as it avoids comparison with the hypothetical general population, and thus requires no assumptions about the representativeness of the sample. We took random samples from the subset to compose groups of n=1 through to n= 24 participants. For each group, we obtained the modal responses (a “plurality” or “relative majority vote”) for all 60 RSPM items and calculated the number of correct responses. As before, this raw test score was then transformed into a collective IQ score. For each group size we also calculated the average IQ of the individual participants, and we identified the highest individual IQ. To ensure reliable results, the randomised sampling was repeated 1000 times, and all results reported values represent averages across the 1000 replicates (Figure 1 outlines the sampling protocols).
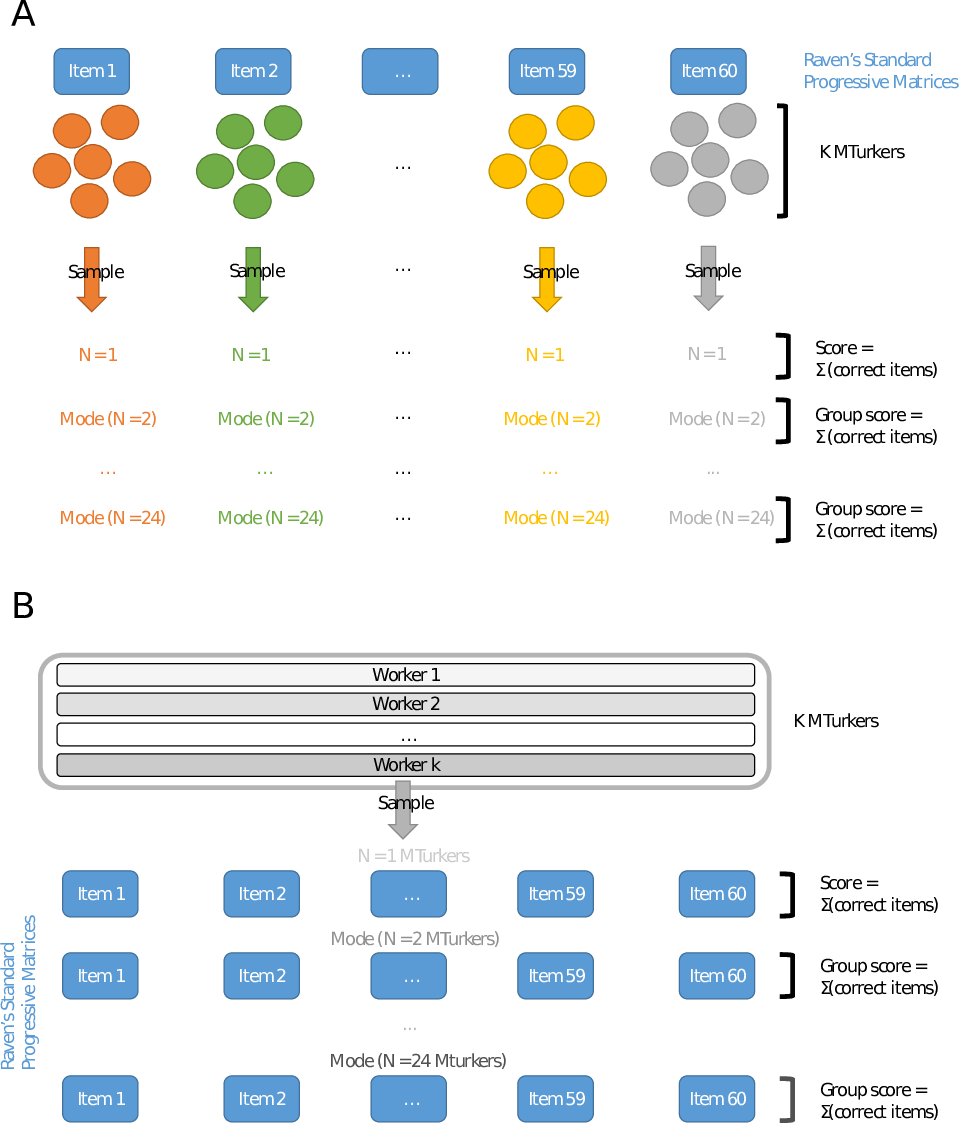
Figure 1: Illustration of the sampling protocols (A) for randomly selected HITs, and (B) for randomly selected participants with 60 complete HITs.
3 Results
3.1 Participants and completed HITs
All participants had 100% reputation ratings on AMT, indicating that they had perfect acceptance rates for their submitted HITs. We obtained a total of 8093 responses from 221 unique workers, who submitted an average of 36.62 HITs each (SD = 24.24). 8.6% of workers only completed a single HIT and 22.6% completed all 60 HITs. Over the 2-week time frame the HITs were open, we received an average of 134.87 responses per HIT (SD = 12.14). The lowest number of HITs were completed for the most difficult items in the SPM (e.g., 96 for item E11 and 101 for E12), which was expected as workers are able to preview the HIT before committing to it.
3.2 Effect of group size
The estimated collective IQ increased non-monotonically with the number of aggregated responses, and diminishing returns are evident even at moderate group sizes (Figure 2). Summing across single responses generates an estimated full-scale IQ that is equivalent to that of an averagely intelligent individual. However, aggregating multiple responses for each test item increases the estimated full-scale IQ substantially. We found that by randomly sampling responses from just 6 workers, aggregation can achieve performance equivalent to an IQ one standard deviation above the mean for the population. This result corroborates the observation made by Kosinski et al. (Reference Kosinski, Bachrach, Kasneci, Van Gael and Graepel2012) that aggregation of individual submissions results in substantial gains in intelligence.

Figure 2: The estimated collective IQ as a function of group size, where groups are composed of randomly selected responses from individual MTurkers. Error bars represent 90% bootstrap confidence intervals.
Each additional individual HIT comes at a cost. We therefore calculated the return on investment achieved by increasing the number of requested responses per HIT. We divided the expected gain in IQ points by the added cost for each group size (number of responses per HIT) relative to the single-HIT (n=1) situation (Figure 3). The largest gain is achieved by investing in just 2 additional requested responses per HIT. For instance, with a six-fold overall cost to complete the full RSPM, each additional $ spent will result in a 1-point increase in the overall IQ.

Figure 3: Return on investment in terms of IQ points for every additional $ spent in virtual groups of varying size.
3.3 Individual vs. collective IQ
The 50 MTurkers that completed the full SPM had an estimated average IQ of 102.66 (SD=15.53, min=69, max=135), which is close to the US national norm and within the range of skilled workers (Kaufman, Reference Kaufman1990). The fact that we found a very weak relationship between the number of HITs completed by a given worker and their average accuracy across all completed HITs (r = .15) appears to rule out that these workers were gaming the system by randomly answering a large volume of HITs. As expected, when item-responses were aggregated on the basis of a plurality vote, the resulting IQ estimate (i.e., the collective IQ) increased significantly with group size (Figure 4). Based on overlap between confidence intervals, we can be reasonably confident that the collective IQ exceeds the average IQ within the group only if the group exceeds 6 members. The collective IQ was not statistically distinguishable from the IQ of the best performing individual within that group for any of the group sizes.
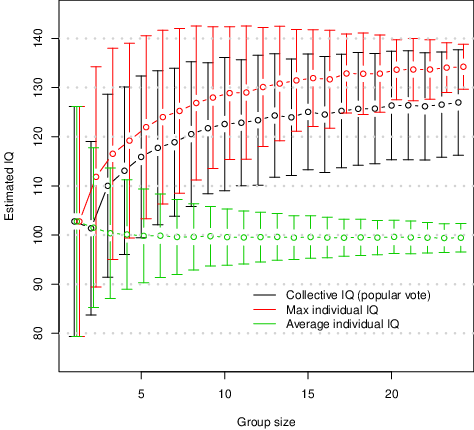
Figure 4: IQ estimates for the subset of individuals who completed all 60 HITs. Direct comparison between collective IQ, the average individual IQ and the highest individual IQ within groups of varying sizes. Error bars represent 90% bootstrap confidence intervals
4 Discussion
In many crowdsourcing applications, a larger task is broken down into many smaller “micro-tasks”, which are outsourced to non-experts. We conducted a partial replication of Kosinski et al.’s (Reference Kosinski, Bachrach, Kasneci, Van Gael and Graepel2012) study to re-examine the hypothesis that the overall task performance would be significantly enhanced by tapping into a wisdom-of-the-crowd effect at the micro-task level. We used a plurality vote method to aggregate multiple responses to individual items from an established and widely validated intelligence test, and combined these answers into a single completed test to obtain a collective IQ estimate. By varying the number of aggregated responses (i.e., the group size), we demonstrate substantial and significant gains in collective IQ, but diminishing returns as the size of the group increases from n=1 to n=24. Furthermore, moderate group sizes may be associated with the greatest return on investment, a finding that is in line with the classic study on group aggregation by Hogarth (Reference Hogarth1978), who observed “optimum” performance levels in groups consisting of 8–12 members. We find that on average, just 8 workers collectively outperform 85% of the population of individual test-takers (Raven, Reference Raven2000), while each IQ point gained produces an additional cost of under 1 US$.
To test the representativeness of these findings, we performed bootstrap sampling and assessed confidence levels around the mean collective IQ, which suggests that to ensure superior performance larger group sizes may be required. Groups of at least 20 workers produce reliable and substantial gains in intelligence (90% CI = 114–132), equivalent to performing at least 1 standard deviation above the population. Our findings thus largely corroborate the observations of the original study, and – importantly – increase confidence in the generality of the group size effect because we were able sample without replacement from a large number of crowdsourced responses to generate virtual groups varying in size. Kosinski et al. (Reference Kosinski, Bachrach, Kasneci, Van Gael and Graepel2012) tested a wider range of effects, including the impact of differential remuneration systems and worker characteristics with n=5 replicated HITs per experimental condition, requiring resampling to test the effect of larger group sizes. Despite finding a slightly more modest effect size, which is a common observation in replication studies (Open Science Collaboration, 2015), our results add to the evidence of robust benefits of collective intelligence in typical crowdsourcing applications.
It should be noted that our study differed in some ways from original study, which may have contributed to the observed difference in effect size. First, we included all 60 test items, rather than employing the common “starting rule” that allows adult test-takers to start at section C and grants full marks for the incomplete sections A-B in the calculation of the total score. Because we did not employ a rejection rule (i.e., workers received a reward for completing the HIT irrespective of whether their answer was correct or not), our approach may have invited more free-riding behaviour. We found indeed, that some responses to the simpler HITs from sections A-B were incorrect, which contributed to lower overall test scores. This is in line with Kosinski et al.’s observations that the risk of rejection substantially increased the collective IQ.
Second, Kosinski et al. (Reference Kosinski, Bachrach, Kasneci, Van Gael and Graepel2012) used a revised version of the IQ test (the RSPM-Plus), which is considered a parallel form with similar psychometric properties. However, it does contain some more difficult items, enabling more precise measurement at higher ability levels and thus the higher maximum collective IQ observed in that study. The RSPM version we used may be limited by ceiling effects. To test the limits of collective intelligence, future work may instead employ either a more challenging version of the Raven’s, such as the Advanced Progressive Matrices, or a different set of intelligence questions.
Another important difference with previous attempts at quantifying the actual gain in quality from crowdsourcing is that our sample included a subset of individuals who had completed the entire IQ test. In contrast to the original study, this allowed us to conduct a direct comparison between individual intelligence and group intelligence. This analysis illustrated that response aggregation on an item-by-item basis results in a collective performance that reliably exceeds the average person within that group, provided the group exceeds 6 members. Irrespective of group size, collective intelligence was never greater than the estimated IQ of the best performing individual within the group. This is likely due to significant heterogeneity in the likelihood of individual group members making a correct judgement on an item. So, in theory, selecting the response from a single excellent worker would result in the best possible overall task performance. However, in crowdsourcing, requesters have very little or no a priori information about the actual expertise or ability of individual workers, nor about the effort expended, which makes the selection of individual optimal performers impractical. Our results support that in this case, the wisdom of the crowd effect can be relied upon to produce equivalent outputs to the best individual in moderately sized groups.
Our findings contribute to a growing understanding of the potential for harnessing the collective intelligence of distributed crowds, but we require further testing and validation under a range of conditions. One limitation of our study relates to the RSPM as our metric. When administered as intended, the test is generally regarded as a good measure of Spearman’s “general intelligence (g)” factor (McKenna, Reference McKenna1984) and test scores typically correlate strongly with more comprehensive intelligence assessments. With its specific sequence of novel problems that increase in difficulty, the test places high demands on the individual’s adaptability and learning capacity as well as their abstract reasoning. However, our crowdsourced application required a deconstruction of the test, an approach which violates the psychometric foundations and the administration rules of the original test. MTurkers completing our HITs could do so in any order and were free to respond to any number and combination of RSPM items. Test scores derived in this way are unlikely to fully capture the underlying cognitive skills as intended by the original test, and the derived IQ estimates should also be interpreted with some caution. Comparison with published norms for the population should similarly be considered as tentative, as the effect of violating the above assumptions is not fully understood.
Nevertheless, due to its relatively short 60-item length, multiple choice architecture and simple structure, the RSPM proved an ideal candidate for decomposition into micro-tasks suitable for crowdsourcing, while also providing a method of translating test performance into an indicator or (collective) intelligence. It is important to note that, because of the way we have operationalised collective intelligence in this study, one should be careful about interpreting it as anything more than “reasoning ability” or “abstract problem solving”. Yet, collective intelligence has typically been defined far more broadly as “groups of individuals doing things collectively that seem intelligent” (Malone & Bernstein, Reference Malone and Bernstein2015). This captures a diverse set of human activities, including face-to-face teamwork, web-based knowledge mapping (e.g., Wikipedia), prediction markets, creative innovation contests, jury decisions and many more. The assessment of collective intelligence in these settings requires a different and more comprehensive approach (for an example, see Woolley, Chabris, Pentland, Hashmi & Malone, Reference Woolley, Chabris, Pentland, Hashmi and Malone2010). The use of crowdsourcing to aggregate many independent judgements represents a very specific application and our findings should be interpreted as illuminating a fraction of the complex potential for human collective intelligence. Future studies should assess whether similar results could be obtained on a variety of cognitive challenges relevant to existing crowdsourcing applications, including reasoning, quantitative estimation, pattern recognition and creative thinking.
To summarise, crowdsourcing platforms such as Amazon’s Mechanical Turk (MTurk) enable businesses, developers, researchers and other requesters to tap into and coordinate distributed human intelligence for tasks that are too computationally intensive for individuals or too complex for computers. With the increase in popularity and the widening user-base, including applications in social science experiments, reasonable questions around quality of crowdsourced outputs have emerged. In this study, we replicate the finding that aggregation of responses to intelligence test items via relative majority vote significantly improves the overall task performance even with relatively small numbers of contributors. Our findings support the mounting evidence for crowdsourcing as an effective tool to tap into and amplify the available intelligence of a diffuse and unknown crowd.





