A method to elicit beliefs as most likely intervals

Abstract

We show how to elicit the beliefs of an expert in the form of a “most likely interval”, a set of future outcomes that are deemed more likely than any other outcome. Our method, called the Most Likely Interval elicitation rule (MLI), asks the expert for an interval and pays according to how well the answer compares to the actual outcome. We show that the MLI performs well in economic experiments, and satisfies a number of desirable theoretical properties such as robustness to the risk preferences of the expert.

1 Introduction

In many instances, uncertainty about future events is the main obstacle to making good decisions. To reduce uncertainty, people frequently consult others who have different or superior information. The consultation may concern tomorrow’s temperature, future market conditions, an interest rate or stock price, or the actions of a politician or business competitor.

We propose a novel method for how to get information from an expert in the form of an interval. Intervals have the the advantage that one need not commit to a specific number nor deal with complex mathematical objects (Mahieu et al., 2014). Moreover, reporting an interval gives the expert the opportunity to provide information about the location of her beliefs and her uncertainty at the same time. Our method relies on monetary incentives. We propose to pay the expert based on the width of the specified interval and whether or not the unknown outcome lies in the interval. These incentives give the expert a reason to think well about her report and allows, given standard assumptions on the expert’s decision making process, to make inferences about her beliefs.

Our payment method incentivizes of the expert to select a “most likely interval”, where any event inside the interval is at least as likely to occur as any event outside the interval. It features an adjustable parameter to influence the width of the reported interval. The inferences from our method are valid for all degrees of risk aversion of the expert, unlike existing elicitation methods (Winkler & Murphy, 1979; Schmalensee, 1976). We show that our scoring rule performs well in laboratory experiments and satisfies several theoretical desiderata.

We now introduce our method in more detail in the context of an example. Suppose a company wants to know what an expert thinks the price of crude oil will be in the next month. The company may ask for a single price estimate, for example the expert’s understanding of the mean, median or modal price. However, a point estimate of the crude oil price provides no information on risk or dispersion, which is vital for contingency planning. At the opposite extreme one may wish to get a complete understanding of the expert’s beliefs and ask for the likelihood of each possible price level (Matheson & Winkler, 1976; Harrison et al., 2013a). While this provides maximal information, it is a time-consuming way to elicit beliefs and presupposes fluency with the mathematical concept of a probability distribution.

An attractive and tractable alternative is to ask the expert for the prices for next month that she regards as being most likely. These prices could be few or many, concentrated or widely dispersed. It seems is reasonable to assume, as we will do in this paper, that the most likely prices are concentrated around some value (i.e. the mode), which means they can be elicited as an interval.¹ Our elicitation method asks for a lower and upper bound of the likely price level, and pays the expert only if the realized price lies in the interval. The reward is a function of the width of the interval, and does not depend on the end points. This implies that the expert has an incentive to specify an interval that contains only the most likely prices, which is why we call our rule the Most Likely Interval elicitation rule (MLI).

Apart from capturing most likely price levels, the company may want to vary the precision of the report. For instance, suppose that company profits are not very sensitive to price deviations and all the company cares about is some indication of the likely outcome. In this case, obtaining a narrow interval with some highly likely events may be optimal even if this means a relatively low confidence that the price will fall in the interval. By contrast, if the company wants to assess the likelihood of an extreme price change, it may prefer to obtain an wide interval with a high degree of confidence.

To address these trade-offs, our elicitation method features a parameter γ that can be chosen freely, and regulates how much the expert is punished for specifying a wide interval. Increasing this penalty will result in a smaller reported set of most likely events and thus will decrease the confidence of the expert that the price will obtain in the specified range. Using a formal model of how the expert makes decisions (i.e. subjective expected utility maximization) we designed the MLI such that each expert will include at least a mass of γ in the interval. We therefore refer to γ as the minimal confidence level.

In order to discipline the expert not to present an interval that is too large, we need to quantify what large means. To this end, we assume bounds on the range of potential outcomes, and the MLI punishes the width as a fraction of this range. For example, when the outcome of interest is a percentage then the natural range is from 0 to 100. In the crude oil example, where these bounds are not given by the problem itself, one can choose the range such that historical observations falls well within them, like 1 and 200 US$ per barrel.

To summarize, our rule guarantees from any expert who maximizes expected utility, that the reported interval only contains those events that the expert thinks are most likely to occur and have a minimal confidence of γ . The actual degree of confidence may be larger than γ, depending on the degree risk aversion of the expert. More risk averse experts will tend to submit larger intervals to guarantee a positive payoff. In principle, one could try to counter act this tendency, with the aim to elicit an interval with confidence close to γ , by designing a different rule for each expert. In most applications there is not enough information about the expert to do so. Therefore, our rule is designed to capture at least confidence γ for any risk averse or risk neutral expert. Experimental evidence indicates that the large majority of people are either risk averse or risk neutral (e.g. Holt & Laury, 2002).

The theoretical research on interval elicitation has focussed on obtaining an interval with a pre-specified likelihood, a so-called credible interval (Murphy & Winkler, 1974). However a credible interval itself does not necessarily reveal any information on what events are most likely as it can contain many least likely events. In fact, we show that none of the previous interval elicitation rules, presented by Winkler and Murphy (1979) and Schmalensee (1976), elicits most likely events.

In contrast to other papers on interval scoring rules, we explicitly compare different rules on the basis of their theoretical properties. Our rule is more generally applicable than existing scoring rules, as it is designed for experts that are either risk neutral or risk averse. In contrast, most of the existing literature on scoring rules focuses on risk neutral experts. Elicitation mechanisms that generalize to all risk preferences exist, but only for means and probabilities (Schlag et al., 2015). Moreover, these mechanisms are substantially more complicated than our interval rule as they require either randomized payoffs (Hossain & Okui, 2013; Schlag & Van der Weele, 2013) or additional elicitations (Offerman et al., 2009), and there is an open debate about the empirical performance of such mechanisms (Selten et al., 1999; Harrison et al., 2013b).

Finally, the empirical research on confidence interval elicitation relies mostly on unincentivized elicitation methods, or ad-hoc scoring rules. For example, Cesarini et al. (2006) reward the subjects if they correctly estimate the hit rate of their previously stated intervals. Blavatskyy (2008) shows that this method is easy to game. Other studies (e.g. Budescu & Du. 2007) simply reward subjects proportional to their accuracy rate, which can be gamed by simply reporting very large intervals regardless of beliefs. The underuse of appropriate incentives is unfortunate, as there is evidence that experimental subjects may be naturally inclined to report different confidence levels than those requested by the experimenter (Yaniv & Foster, 1997), and that appropriate incentives improve accuracy of forecasts (Krawczyk, 2011).

This article proceeds as follows. The next section introduces the elicitation environment and the MLI. Sections 3 and 4 provide examples of how to implement the rule and discuss potential applications. Section 5 provides a more formal discussion of the properties of the MLI, and Section 6 compares those properties to those of other scoring rules in the literature. Section 7 discusses the robustness of the rule to the assumptions we have made, and provides some extensions. Section 8 concludes.

2 The elicitation environment and the MLI

Consider an unknown event characterized by value x, realized at some given time in the future, where the domain of x is [ a, b] . Often, a and b will be given by the problem, for example when x is a percentage. If this is not the case, then the boundaries can be chosen such that it is expected that the expert believes that x falls within this range for sure, with the understanding that any x outside the range will be treated as if it was at the boundary. To obtain the beliefs of the expert about the values of x, we ask for an interval [ L, U] ⊆ [ a, b] , and commit to how we will pay the expert on the basis of the interval and the realized outcome.

The Most Likely Interval elicitation rule (MLI) pays the expert for her reported interval whenever the true realization lies in the interval she submitted, where the payment is strictly decreasing in the width of the reported interval. The rule has a free parameter γ ∈ (0,1). The payment received when submitting and interval [ L, U] when value x is realized is denoted by S _M( L, U, x), and depends on the width W= U− L of the interval as follows

where g=1−γ /γ . If γ =1/2 then it obtains its simplest, linear form:

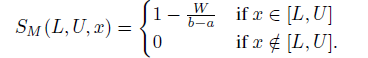
The properties of the rule are invariant to any affine transformation of S _M. This means that one can regulate the amount paid out to the expert by multiplying the payoffs with an appropriate number. The rule can be applied to any random variable X that has support in [ a, b]. In particular, it also applies to transformations of X, like log( X) or to cX+ d, as long as one transforms the boundaries a and b in the same way.

We designed the MLI to be able to make inferences from the elicited interval about the beliefs of the expert under some assumptions on how the expert makes choices. Suppose the beliefs of the expert of a random variable of interest X can be described by the cumulative density function F _X. We assume these beliefs satisfy the following two assumptions: (i) F _X is a continuous distribution with at most one mass point and density f. (ii) F _X is single peaked, which means that the likelihood of an event decreases as one moves away from an event that has the highest likelihood. More formally, X is single-peaked if there exists x ₀ such that f is increasing in x for x≤ x ₀ and decreasing in x for x≥ x ₀. Any value x ₀ with this property is called a mode of X. ² We believe the assumption of single-peakedness makes sense under many circumstances. In cases where it does not, the MLI can easily be extended to allow for multiple intervals as outlined in Section 7.

Suppose now that the interval specified by the expert, denoted by [ L ^∗, U ^∗] , is chosen exclusively on the basis of monetary payoffs S _M. Then the expert is best off by placing an interval with width W within the range [ a, b] where it “covers” or contains the true event with the highest probability. As beliefs are single-peaked, the reported interval [ L ^∗, U ^∗] will contain all values with a likelihood above some threshold, and thus contains a mode of X. We refer to this key property as “most likely”.

The width W ^∗= U ^∗− L ^∗ of the reported interval contains further information about the expert’s uncertainty. To see this, consider the dependency of MLI on the width W. Increasing W increases the likelihood of being paid but decreases the payment itself. For small values of W, when the expert is very certain about what will happen, an increase in W/( b− a) leads to an decrease in payment approximately equal to − g. In Figure 1, we plot the payment as a function of the width W of the interval for three cases, g=1/2, 1 and 2, so for γ =2/3, 1 and 1/3, and a=0 and b=1.

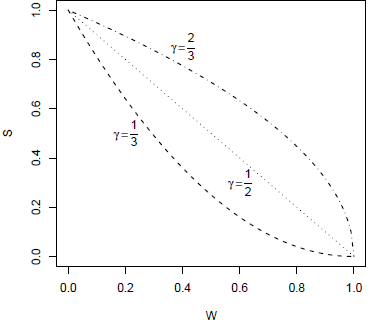
Figure 1: Relation between the width W (on the x-axis) and payment S _M (on the y-axis) for different values of γ and for a=0 and b=1.

As γ increases, and g decreases, the incentives to increase W become stronger. When γ is small then the expert has the highest incentives to report a small interval. Choosing a small value for γ can be of interest when one wishes to obtain a point prediction about what is most likely to happen, but one does not wish to force the expert to commit to a specific number. When γ is large then the interval will tend to be large, and the events that are not included in the interval can be considered ‘extreme’ or unlikely events.

If we assume that the expert is a subjective expected utility maximizer with respect to the payoffs S _M, we can also make inferences about the total or joint probability that the realization x will be in the interval. Since the parameter γ influences the width, it also influences this probability. In particular, if the expert is either risk neutral or risk averse, the interval will cover at least the mass γ of the expert’s beliefs, as we will show in Section 5. More formally, P _{F X}( X∈ [ L ^∗, U ^∗] ) ≥ γ . This “coverage” property means that the MLI provides information about the expert’s confidence in the reported interval. In Section 5, we also show how more dispersed beliefs translate to wider intervals. In this sense the width captures the expert’s degree of uncertainty.

To summarize, the MLI can extract information about the expert’s beliefs in terms of location, confidence and degree of uncertainty.

3 Implementation: An example

In this section, we illustrate the implementation of the MLI in an experimental context. To do so, we analyze the experiment by Galbiati et al. (2013), in which both co-authors of the current paper were involved and that saw, to our knowledge, the first experimental implementation of the MLI.³

Experiment outline.

The experimental context was a strategic game between two players, called the minimum effort game. In this game, both players had to choose an “ effort level” e, which could be any number between 110 and 170. The payoffs of π _i of player i=1,2 depended on the effort of both players as follows

(2)

Thus, each player was rewarded according to the minimum of the two effort levels, while “paying” a cost proportional to her own effort.⁴

As we explained to the participants in the instructions, it is optimal for each player to match the effort level of the other player. If the own effort level exceeds that of the opponent, one could increase payoffs by decreasing effort. When effort is lower than that of the opponent, one could increase payoffs by increasing efforts.⁵ Thus, a crucial determinant of a player’s actions is what effort s/he thinks the other player will choose. Moreover, the nature of uncertainty about the other’s effort matters, because undershooting the other’s effort is less costly than overshooting it. This makes the MLI a suitable elicitation method. We chose γ =0.5 to maximize the simplicity of the rule, and scaled the payoffs in order to balance them with the earnings from the effort decision.

The subjects played two rounds of this game. The second round was played without feedback about the outcomes of the first round. We consider two experimental conditions of the experiment, which differed only with respect to the details of the second round. In the Control condition, 30 participants played exactly the same game in the two rounds. In the Incentive condition, with 34 participants, we implemented a small penalty for deviating from the maximum effort of 170. Formally, we added to the payoffs in (2) a component −1/2(170− e _i). This implied that higher effort became more attractive as it became less risky (although still suboptimal) to overshoot the opponent’s effort.

Belief elicitation instructions. Beliefs were elicited in both rounds of the game, simultaneously with the effort choice. The MLI was introduced to the experimental participants with the following instructions.

Guessing the other’s choice

We now ask you to make a guess about the number chosen by the other player. The guess is made by specifying a range (given by its lower bound L and its upper bound U ) in which the other player’s choice is believed to belong. The earnings in tokens of either player 1 or player 2 from making this guess are determined as follows. A wrong guess (the actual number chosen by the other player falls outside the specified range) yields nothing. A correct guess (the actual number chosen by the other player lies within the specified range) yields 15% of the difference between 60 and the width of the range U − L . Therefore the smaller the specified range, the higher the earnings if the guess is correct. However, a smaller range also increases the risk that the guess is not correct, in which case no tokens are earned. ⁶

Note that tokens where converted to real money at the end of the experiment.

Results.

First, we investigate if effort forecasts elicited with the MLI were accurate. Note that the MLI elicits individual subjective beliefs that need not conform to the actual frequencies. Nevertheless, we can compare the average elicited interval to the actual distribution to understand how well-calibrated the subjects are on an aggregated level.

Figure 2 shows the actual frequency distribution of effort in the Incentive condition (light/red line) and to the Control (black line), which present the “right” answer for subjects to estimate. In line with the theoretical predictions spelled out in Galbiati et al. (2013), the distribution of effort indeed went up in the Incentive condition relative to the Control. The shaded areas in Figure 2 show the average intervals specified by the participants in the second round in the different conditions. As is clear from the figure, the location of the intervals moved in line with the theoretical predictions. What is more, in both cases, the average interval captures the mode of the distribution, and are not very far away from capturing only the most frequent effort levels. From these results it appears that the average intervals are well-calibrated. This is a useful property in applications and suggests that aggregated intervals have favorable properties, the theoretical analysis of which we leave to future research.

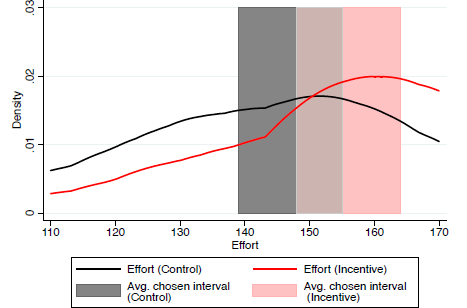
Figure 2: Distribution density plots of effort (thick lines) measured in units 1/ e where e is effort. The shaded areas represent the corresponding average estimated interval in the Incentive and Control condition.

Second, we investigate the width of the belief interval. The average widths of the chosen interval in the first round was about 18 points, and was actually slightly higher in the Incentive condition. What interests us most is whether the width of the interval responds to the incentives in the second round of the game. Effort moved up in the Incentive condition and the standard deviation of effort declined from 19.4 in the Control to 17.5 in the Incentive condition. Thus, as effort became more predictable, it is natural to expect that the dispersion of beliefs goes down in the Incentive condition. As we will show in Section 5, this implies that the optimal interval width declines. Figure 3 shows the change in the mean width of the intervals between the rounds, with 95% confidence intervals. Interval widths remained virtually unchanged in the Control condition, while they declined substantially (by 26%) in the Incentive condition.

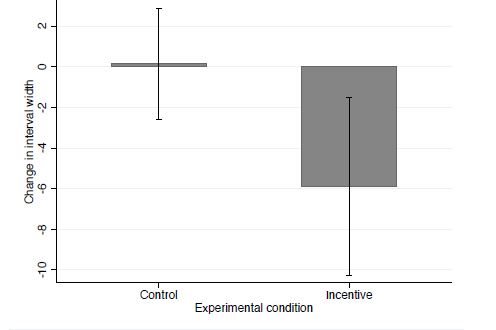
Figure 3: Change in the average interval width between the first and second round in the Incentive and Control condition, with 95% confidence intervals.

Finally, we investigate the relation between the beliefs and effort that are elicited from the same person. Such a connection demonstrates that people act upon their belief, and support the conclusion that we elicited a relevant variable. Figure 4 shows the relation between effort ( x-axis) and beliefs ( y-axis), pooling both experimental conditions. The chosen belief intervals are shown in grey. As is apparent from the black lines fitted to capture the lower and upper bound of the belief interval, higher and more precise beliefs are associated with higher efforts. Moreover, looking at the dots that indicate the actual effort choice, we see that effort is inside the belief interval in most cases. This is what one would expect in this strategic situation where each player has incentive to match the effort level of the other player.

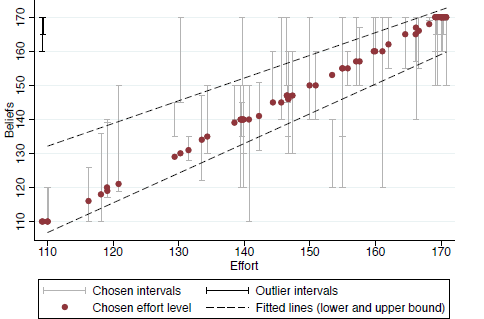
Figure 4: This graph shows the relation between effort ( x-axis) and beliefs ( y-axis), pooling both experimental conditions. The chosen belief intervals are shown in grey, except two outliers at the top left, shown in black. The two fitted lines pertain to the upper and lower bound of intervals respectively, ignoring the two outliers. Dots indicate the effort choice. These dots do not lie exactly on the 45 degree line as we added some noise to avoid overlays of data points.

In summary, we incentivized subjects with the MLI to predict the choice of their opponents in a strategic environment. We found that, first, average intervals specified by the participants include the mode of the actual distribution and are not far from capturing the most likely events. Second, both the width and the locations of the intervals respond to our experimental manipulation in a way that was in line with theoretical predictions. Third, there is a robust relationship between the specified beliefs about the opponents and the strategic choices in the experiment. These findings indicate that the MLI is a reliable method to elicit beliefs in this context.

4 Applications

In this section we provide an overview of potential applications of the MLI. To do so, we review applications of MLI in previous experimental work and discuss potential applications in finance, management and other settings.

4.1 Applications in experiments

Based on earlier versions of this paper, the MLI has been implemented in economic experiments to elicit expectations about a diverse set of variables. These experiments demonstrate the flexibility of the MLI both in the type of expectation that can be elicited and in the way that the resulting data can be analyzed.

Elicitation has taken place in both strategic and non-strategic settings. As an example of the latter, Peeters and Wolk (2014) use the MLI to elicit repeated forecasts about realizations of a random variable. Examples of strategic settings are the use of the MLI to elicit beliefs about contributions to a public good (Cettolin & Riedl, 2013) or a risk sharing fund (Tausch et al., 2014). The MLI has also been used to elicit beliefs about characteristics of other experimental participants, such as their beliefs (Peeters et al., 2015) or risk aversion (Cettolin & Riedl, 2015).

When it comes to analysis of the data, some authors use the midpoint of the interval as a measure for the location of beliefs, either as an explanatory variable in regressions (Cettolin & Riedl, 2013; Peeters et al., 2015) or as the object of non-parametric comparisons to assess the importance of beliefs in different experimental conditions (Tausch et al., 2014; Cettolin & Riedl, 2015). With respect to the width of the interval, Peeters et al. (2015) uncover differences in the uncertainty of participants in different strategic roles. Cettolin and Riedl (2013) find a positive correlation between a measure of risk aversion of the participants and their elicited interval width, a correlation which is significant at 1%.⁷ Finally, Peeters and Wolk (2014) demonstrate how to aggregate the elicited intervals of multiple individuals and show that the calibration of forecasts about the realization of a random variable improves with the number of individuals.

One potentially interesting application of the MLI relates to measuring overconfidence with intervals. Countless studies show that 90% confidence intervals elicited without incentives are accurate much less than 90% of the time (Russo & Schoemaker, 1992; Moore & Healy, 2008). Yaniv and Foster (1997) argue that participants do not necessarily report the confidence levels requested by the experimenter, but tend to make their own normative trade-offs between informativeness and accuracy. Appropriate incentives, such as those provided by the MLI could help reduce the miscommunication between experimenter and participant. Indeed, Krawczyk (2011) shows that providing incentives for truthful elicitation improves results. In Section 6, we argue that the MLI may be a good alternative to the incentives used in Krawczyk (2011), although this remains to be tested empirically.

4.2 Real world applications

Estimations in the form of intervals play a role in many applications. Perhaps the most salient one is in weather forecasting, where they are common in forecasts of temperatures. Indeed, a literature exists in weather forecasting that investigates the interval reports of weather forecasters (e.g. Hamill & Wilks, 1995). Forecasts of financial variables such as inflation or growth rates are also often given as confidence intervals, since risk plays an important role in financial decisions. For instance, trader’s buying and selling strategies depend on corridors in which prices are expected to lie. The MLI can be used to elicit such a corridor, by identifying L and U by parallel lines that have distance U− L. Central banks can use the MLI to elicit intervals from economic experts about future unemployment and inflation, and use these estimates construct contingent policies.

Financial officers in businesses can use interval forecasts to plan continent pricing strategies or sales targets. Future prices and sales depend on many factors unknown to managers, who could elicit intervals from employees in order to improve the realism of targets. Even current performance may be hard to measure, and could be elicited as interval estimates from employees. In this context, the free parameter γ in the MLI is useful to communicate the desired level of precision. In Section 7 we also explain how, with a small modification, one can also use the MLI to elicit estimates of tail risks, like the common measure Value at Risk.

Interval forecasts elicited with MLI may also represent a useful complement to classic Confidence Intervals (CIs) derived from statistical models, which are one of the most popular statistical tools for understanding uncertainty. The two intervals differ in several ways. First, while CI refer to the information in the data about the true state, elicited intervals refer to the information contained in the beliefs of an expert. Second, while CIs derived from statistical models would contain the outcome with probability equal to γ, the MLI elicits most likely intervals which contain the outcome with probability of at least γ.

5 Theoretical properties of the MLI

The previous sections have shown how one can elicit beliefs using the MLI and informally discussed some of the properties of the elicited interval. In this section, we discuss the theoretical properties of MLI and the associated inferences more formally and extensively. Our companion paper (Schlag & Van der Weele, 2014) provides additional discussion of the theoretical aspects of these properties. All proofs are contained in the Appendix.

We consider the optimal response of expert endowed with preferences over ℝ that admit an expected utility representation, denoted by u. An interval scoring rule S is a mapping from [ a, b] ³ to ℝ⁺ where S( L, U, x) is the payoff that the expert receives after reporting the interval [ L, U] and the event x is realized. Let [ L ^∗, U ^∗] =[ L ^∗( F _X, S, u) , U ^∗( F _X, S, u) ] denote be the interval chosen by an expert with utility u and beliefs F _X when paid by the rule S. Let W ^∗( F _X, S, u) = U ^∗( F _X, S, u) − L ^∗( F _X, S, u) be its width and let M ^∗( F _X, S, u) = P _{F X}( X∈ [ L ^∗( F _X, S, u) , U ^∗( F _X, S, u) ] ) be the probability that the event belongs to the elicited interval.

The expert’s reported interval depends on her beliefs and risk preferences. Inferences from interval elicitation that depend on the assumption of risk neutrality of the expert should be approached with caution. Holt and Laury (2002) present evidence that most experimental subjects are risk averse. Armantier and Treich (2013) and Offerman et al. (2009) show that most subjects behave as if they are risk averse in the context of belief elicitation. Hence we choose to model the expert as being either risk neutral or risk averse and consider only concave u.

We first show that an optimal interval always exists.

Proposition 1 For any single-peaked F _X there exist L ^∗ and U ^∗ with a≤ L ^∗≤ U ^∗≤ b such that u( S _M( L ^∗, U ^∗, X) ) =sup_{L, U: a≤ L≤ U≤ b} u( S _M( L, U, X) ).

The result is obtained by showing that u( S _M( L, U, X)) is upper semi-continuous. Then, by the extreme value theorem, it attains a maximum on the compact domain.

In what follows we discuss inferences from the MLI, where we separate inferences in terms of location and dispersion. Location refers to where the interval is located and the properties of the boundaries. Dispersion refers to the width of the interval, as measure of vagueness of the report and uncertainty of the expert.

5.1 Inferences about the location of beliefs

We designed MLI to get an understanding of what the expert thinks is most likely to happen. The more likely events should be contained in the interval, the less likely not, a property we call “most likely”.

Definition 1  (Most Likely).  We say that an interval scoring rule S elicits most likely events for X and u if there exists a z such that[ L ^∗, U ^∗] ={ x: f( x) ≥ z}.

We obtain the following result.

Proposition 2  The MLI elicits most likely events for all single-peaked X and all u .

The proof of this result is trivial: If the interval does not contain the most likely events, the expert could improve his expected payoff by moving the interval. As we show below, changing the penalty parameter for the width of the interval will change the set of most likely events that is elicited, but in every case the events in the interval are more likely than those outside.

The following result follows directly from Proposition 2.

Corollary 1   The interval[ L ^∗, U ^∗] elicited with the MLI contains a mode of X for any single-peaked X and any u.

We do not know of any other scoring rule that elicits the mode of a continuous distribution. Note that the MLI will not necessarily cover all modes of X. For example, if X is uniformly distributed on [ a, b] then each x∈ [ a, b] is a mode of X.

In addition, we can prove that the interval will contain another common location parameter if the penalty for a high width is relatively low.

Proposition 3   Ifγ ≥ 1/2, the interval[ L ^∗, U ^∗] induced by MLI contains the median for all single-peaked X and all concave u .

This result is a direct consequence of the fact, proved below, that the interval will contain the realization with probability of at least γ.

One may wonder whether the interval induced by MLI will also include the mean of X. The example below shows that MLI does not cover the mean for sufficiently skewed distributions. For such distributions the mean does not necessarily provide a good indicator of the concentration of mass, so we consider its elicitation an alternative objective to eliciting the most likely events.

Example 1 Consider ε >0 and assume that X is distributed such that Pr ( X=0) =1−ε and f _X( x) =ε for x∈ ( 0,1] . Note that this distribution is single-peaked and has expected value EX=ε /2. Since MLI elicits the most likely events, L ^∗=0. The first order condition for U is ε ( 1− U ^∗) =( 1−γ /γ ) ( 1−ε + U ^∗ε ) . It follows that U ^∗= max{0,γ −(1−γ )}. Thus, if γ +ε ≤ 1 then U ^∗=0 and the interval elicited under MLI does not include the mean of X. ▪

To summarize, the interval elicited under the MLI contains the mode, the most likely events and the median if γ≥1/2. For skewed distributions it does not necessarily contain the mean of the random variable. Note that the midpoint of the interval plays no special role in the theory. However, it is a useful measure of the location of the interval and can be used together with the width, for instance in regressions.

5.2 Inferences about the dispersion of beliefs

Apart from location of typical or most likely events, we would like to draw inferences about the dispersion of the beliefs of the expert. We distinguish between two types of dispersion, absolute and relative. Absolute dispersion refers to the amount of mass contained in the interval for a given expert. Relative dispersion refers to differences in dispersion between different experts or between the same expert in different conditions.

5.2.1 Absolute dispersion

As argued in the introduction, in applications it will often be useful to know how likely the expert thinks that the realized event will belong to the interval. Specifically, it would be useful to understand the relation between the absolute dispersion and the choice of γ . Ideally we would like to elicit a γ · 100% credible interval (Murphy & Winkler, 1974). A rule that elicits a credible interval may be referred to as a “proper” rule. However, it is not possible to design a rule that is proper for different degrees of risk aversion of the expert. The reason is that sufficiently risk averse experts will always specify larger intervals to secure a positive payoff. Since we aim for a single rule that allows inferences for any degree of risk preferences, we consider the weaker property of “coverage” (Casella & Hwang, 1991).

Definition 2  (Coverage)   An interval scoring rule S has “coverageγ ” for X and u if M ^∗( F _X, S, u) ≥ γ .

Thus, coverage requires that the optimal interval contains at least γ · 100% of the mass, so the expert is at least γ · 100% confident that the outcome will occur within the interval. Note that this definition of coverage, like the definition of the confidence intervals in statistics, implies that a rule with coverage γ also has coverage γ ^′, for all γ ^′≤ γ . We obtain the following result.

Proposition 4   The MLI has coverageγ for all single-peaked X and all concave u.

The fact that coverage increases with γ is intuitive, since a higher γ translates into a lower penalty for widening the interval. We give a short sketch of the intuition behind the proof, which is contained in the Appendix A. Denote by M( w) the maximal subjective probability that can be covered by an interval for a given width W= w. Then the maximal expected utility of specifying an interval with width w is equal to u( h( w)) M( w) where h( w) =( 1− w) ^{1−γ /γ}. The first order condition related to the optimal choice of the width W is:

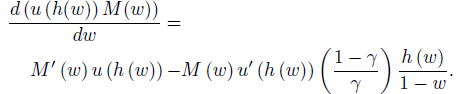
The first argument of the RHS is the marginal benefit of expanding the interval, which consists of an increased likelihood of capturing the realized event. The second term is the marginal cost of doing so, which consists of a decreased payment if the realized event is in the interval. We know that u is concave (by assumption) and M is concave in w because of single-peakedness. Using these facts, we show in the proof that M( w)<γ implies that the derivative with respect to the width is positive, so that the expert would like to expand the interval.

5.2.2 Relative dispersion

In some applications it will be useful to use the elicited reports for the purpose of comparing the beliefs of different experts or the beliefs of the same experts at multiple points in time. It turns out that the width of the elicited interval can provide a useful measure for both types of comparisons.

First, we show that the width of the interval increases when beliefs become noisier in the following sense.

Definition 3  X _ε is noisier than X if

where ε ∈ [0,1]and Y is uniformly distributed on [ a, b].

This definition says that noise increases if beliefs are closer to the uniform distribution. We consider noisiness to be an intuitive measure of uncertainty, since the uniform distribution can be interpreted as the case where the expert has no information. Note that under this notion of noisiness, unlike a mean preserving spread, the expected value typically changes when noise increases.

Proposition 5   Assumeγ ≥ 1/2.If X ^′ is noisier than X , then W ^∗( F _X, S _M, u) ≤ W ^∗( F _{X ^′}, S _M, u) holds for all single-peaked X and concave u.

Proposition 5 establishes that an increase in noise translates into a (weakly) wider reported interval.

Second, one would expect that experts who are more risk averse will specify larger intervals, since they are more worried about getting a payoff of zero. This intuition can be formalized as follows. We say that ũ is more risk averse than u if there is a concave function g such that ũ ( x) = g( u( x) ) for all x.

Proposition 6   Assumeγ ≥ 1/2.Ifûis more risk averse than u , then W ^∗( F _X, S _M, u) ≤ W ^∗( F _X, S _M,ũ) for all single peaked X.

Proposition 6 tells us that a more risk averse expert will always specify a weakly larger width. ⁸

To summarize, the width of the interval allows two kinds of comparative inferences. When u can be reasonably held constant, for example by repeatedly eliciting intervals for the same expert over time, one can falsify the hypothesis that the beliefs of an expert become noisier. This is important, since the noisiness of the distribution can be interpreted as a proxy of uncertainty, which will be relevant in many applications. In the same vein, if X can be assumed to be constant across different experts, for example across experimental participants who received the same information, the interval width gives information about their relative degrees of risk aversion.

The results from experimental studies using the MLI discussed above confirm these comparative statics. In the experiment discussed in Section 3, average interval widths (measured within-subject) declined substantially in a treatment where uncertainty about the other player’s actions was hypothesized to go down. As discussed in Section 4, Cettolin and Riedl (2013) find a positive and strongly significant correlation between a measure of risk aversion and interval width.

6 Comparison to other interval scoring rules

The literature on scoring rules for belief elicitation focuses on the elicitation of point beliefs rather than theless, we have found two scoring rules for interval elicitation in the literature that have been justified in terms of desirable properties.⁹ Winkler and Murphy (1979, WM79 hereafter). It is applied in Hamill and Wilks (1995) and Krawczyk (2011), and discussed in some detail in Gneiting and Raftery (2007). Up to an affine transformation, this rule is given by

where 1_E is an operator that is 1 if the event E is true and 0 otherwise. In words, this rule punishes the expert for specifying a larger interval width, and for the distance of x from the interval bound if x is outside the interval.

The second scoring rule is proposed in Schmalensee (1976, S76 hereafter). Up to an affine transformation, it is given by

This rule is similar to S _WM79, but it adds an extra penalty if the realization is inside the interval, but away from the mid-point.

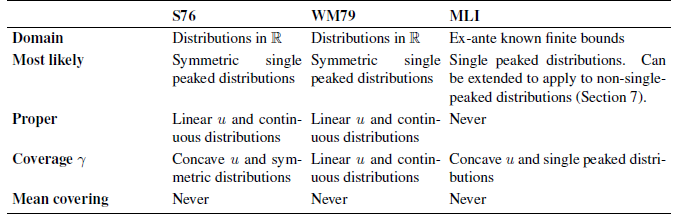
The main reason S _S76 and S _WM79 have been discussed in the literature is that they are proper if the expert is risk neutral. Winkler and Murphy (1979) show that S _WM79 elicits the and quantiles if the decision maker is risk neutral, thus tracking the mass in the tails of the distribution. As we argued above, risk neutrality is likely to be violated in experimental settings, limiting the usefulness of this property. We prove in our companion paper (Schlag & Van der Weele, 2014) that both rules satisfy the coverage criterion.

However, neither S _S76 nor S _WM79 elicits the most likely events. ¹⁰ To see this, consider a skewed distribution with density , depicted in Figure 5. The bottom of the figure shows the optimal intervals for a risk neutral expert under MLI, S _S76 and S _WM79.

Figure 5: Optimal intervals for MLI, S67, and WM79 when γ =0.5.

Table 1: Overview of the assumptions underlying the properties of the different interval scoring rules.

The figure shows that S _S76 and S _WM79, do not capture the most likely events, as the events to the left and outside the interval are more likely to occur than those inside the interval. Thus, one cannot generally infer from the stated interval which events the expert thinks are most likely. This result holds for all γ <1. The reason is that these rules do not reward the expert for a correct prediction, but ‘punish’ the expert if the realization is very far from the chosen interval bounds. This means that the expert does not want to specify an interval too far away from either end of the range.

Table 1 summarizes the properties of the different scoring rules.

7 Extensions

In this section we discuss some of the assumptions that we have made on the elicitation environment, and propose some extensions of our rule.

7.1 Finite outcome spaces

In many applications the outcome x belongs to a finite set. To capture this, assume that x belongs to X ={ a+δ, a+2δ ,.., a+ nδ = b} where δ >0 is the distance between any two points in the grid. In such cases we still propose to use MLI. It turns out that all properties continue to hold, except one can no longer guarantee coverage γ but only coverage γ −ε , where ε is a decreasing function of δ.

7.2 Multi-peaked distributions and MLMI

Sometimes beliefs may reasonably be expected to have more than one peak. Our method can be adapted to allow for this possibility. Give the expert the opportunity to submit multiple nonintersecting intervals. Pay the expert when the event lies in one of the intervals the amount specified by S _M given in (1) except that W now is equal to the sum of the widths of all intervals reported by the expert. We call the resulting rule the Most Likely Multiple Interval elicitation rule, short MLMI. All results carry over to this setting. The only difference is that now beliefs can distributed according to any continuous distribution.

7.3 Eliciting tail risk and the OMLI

As we remarked in Section 4, the MLI can also be used to understand tail risks. The idea is to elicit an interval in the domain of losses, where one fixes the lower bound of the interval at a loss of 0. The expert thus only chooses the upper bound U, but payments are otherwise the same as for the MLI, resulting in the One-sided Most Likely Interval elicitation rule (OMLI).

As an example, one can follow this procedure to elicit an upper bound for the Value at Risk (VaR). p-VaR for a given probability p and a given time horizon is a popular measure of risk of a portfolio. It is defined as the threshold loss y, such that the probability that the loss on the portfolio exceeds y is equal to p. To elicit an upper bound for y, ask the expert for a value U, and pay according to the MLI if losses fall in the interval [ 0, U] . Here, the lower bound of the interval is fixed at L=0. To implement a given value of p, set γ =1− p. Given the coverage property of the MLI, the value U then constitutes an upper bound on the p-VaR as believed by the expert.

7.4 Improved precision and the TMLI

Another criterion to select amongst interval scoring rules is to pick the one that pins down the mass γ with most precision. To get maximum precision, one would like to pick the rule that implements the smallest width of the expert’s optimal interval for given coverage γ, beliefs F _X and preferences u. The question is how one should aggregate over all possible beliefs and preferences. Casella and Hwang (1991) propose to measure precision in terms of the ‘worst case’ belief distribution that induces the maximal interval width, and select the rule that minimizes this maximal width.

Definition 4  (Minmax width)   S with coverageγ attains “minmax width within S ” if there is no scoring ruleS∈ S with coverageγ such that

The problem with the scoring rules discussed above is that when the expert is very risk averse, she will specify intervals that are larger than necessary to cover γ . In order to counter this tendency, one can specify a maximum width of the interval for which the expert can earn positive payoffs. The resulting Truncated Most Likely Interval elicitation rule (TMLI) is given by

Thus, there is no payment if the expert specifies an interval larger than a fraction γ of the range [ a, b]. The rationale is that for the worst-case uniform distribution, this fraction covers exactly γ , while for other single-peaked belief distributions one can cover γ in a smaller interval. Thus, the TMLI punishes the expert for specifying a range that is larger than necessary to obtain coverage, and in fact obtains minmax width amongst all interval scoring rules with coverage γ. ¹¹

8 Conclusion

Eliciting belief intervals is a good way to gain a quick and intuitive understanding of both the events that the expert thinks likely to occur and the dispersion of an expert’s beliefs. The Most Likely Interval elicitation rule’ is easily implementable, performs well in economic experiments and satisfies a number of desirable theoretical properties. On the basis of these qualities, we believe the MLI can be a valuable tool for practitioners and experimentalists.

The appeal of confidence intervals merits further work into interval scoring rules. On the empirical side, it will be necessary to compare the performance of these and other interval scoring rules. On the theoretical side, there are further questions about the trade-offs in designing interval scoring rules, for example between the complexity of the rule and its desired theoretical properties (Schlag & Van der Weele, 2014). The aggregation of different intervals is also an important research area. While the results reported in Section 3 and in Peeters and Wolk (2014) indicate that aggregated intervals are reasonably well-calibrated, the theoretical properties of these aggregates are not yet understood.

Another interesting topic is how to combine incentives for truthful reporting with ex-post rewards for well-calibrated forecasts. A naïve approach would be to collect a number of realizations from the random process under consideration and then use the MLI or one of the other interval scoring rules to compare and score forecasts from several experts.¹² However, such rewards may destroy incentives for truth telling. For instance it is not clear how scoring on the basis of multiple realizations changes the the incentives, as experts may hedge their bets between different elicitations. Another problem is that competition between experts may induce them to become risk seeking, and specify smaller intervals or even unlikely events.