Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-15T10:55:32.377Z Has data issue: false hasContentIssue false
  • English
  • Français

A framework for belief revision under restrictions

Published online by Cambridge University Press:  12 September 2022

Zhiguo Long Open the ORCID record for Zhiguo Long [Opens in a new window] ,
Hua Meng Open the ORCID record for Hua Meng [Opens in a new window] ,
Tianrui Li ,
Heng-Chao Li  and
Michael Sioutis
Zhiguo Long
Affiliation:
School of Computing and Artificial Intelligence, Southwest Jiaotong University, Chengdu, China
Hua Meng
Affiliation:
School of Mathematics, Southwest Jiaotong University, Chengdu, China E-mail: menghua@swjtu.edu.cn
Tianrui Li
Affiliation:
School of Computing and Artificial Intelligence, Southwest Jiaotong University, Chengdu, China
Heng-Chao Li
Affiliation:
School of Information Science and Technology, Southwest Jiaotong University, Chengdu, China
Michael Sioutis
Affiliation:
Faculty of Information Systems and Applied Computer Sciences, University of Bamberg, Bamberg, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

Traditional belief revision usually considers generic logic formulas, whilst in practical applications some formulas might even be inappropriate for beliefs. For instance, the formula 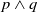$p \wedge q$ is syntactically consistent and is also an acceptable belief when there are no restrictions, but it might become unacceptable under restrictions in some context. If we assume that p represents ‘manufacturing product A’ and q represents ‘manufacturing product B’, an example of such a context would be the knowledge that there are not enough resources to manufacture them both and, hence, 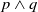$p \wedge q$ would not be an acceptable belief. In this article, we propose a generic framework for belief revision under restrictions. We consider restrictions of either fixed or dynamic nature, and devise several postulates to characterize the behaviour of changing beliefs when new evidence emerges or the restriction changes. Moreover, we show that there is a representation theorem for each type of restriction. Finally, we discuss belief revision of qualitative spatio-temporal information under restrictions as an application of this new framework.

Type
Research Article
Information
The Knowledge Engineering Review , Volume 37 , 2022 , e8
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alchourron, C. E., Gärdenfors, P. & Makinson, D. 1985. On the logic of theory change: partial meet contraction and revision functions. Journal of Symbolic Logic 50(2), 510–530.CrossRefGoogle Scholar
Alirezaie, M., Längkvist, M., Sioutis, M. & Loutfi, A. 2019. Semantic referee: a neural-symbolic framework for enhancing geospatial semantic segmentation. Semantic Web 10(5), 863–880.CrossRefGoogle Scholar
Benferhat, S., Lagrue, S., Papini, O. et al. 2005. Revision of partially ordered information: axiomatization, semantics and iteration. In International Joint Conference on Artificial Intelligence, 376–381.Google Scholar
Booth, R. 2002. On the logic of iterated non-prioritised revision. In Conditionals, Information, and Inference, International Workshop, WCII 2002, Hagen, Germany, 86–107.Google Scholar
Booth, R., Fermé, E., Konieczny, S. & Pérez, R. P. 2012. Credibility-limited revision operators in propositional logic. In International Conference on Principles of Knowledge Representation and Reasoning, 116–125.Google Scholar
Boutilier, C. 1996. Iterated revision and minimal change of conditional beliefs. Journal of Philosophical Logic 25(3), 263–305.CrossRefGoogle Scholar
Condotta, J. F., Kaci, S., Marquis, P. & Schwind, N. 2009a. Merging qualitative constraint networks defined on different qualitative formalisms. In International Conference on Spatial Information Theory, 106–123.Google Scholar
Condotta, J. F., Kaci, S., Marquis, P. & Schwind, N. 2009b. Merging qualitative constraints networks using propositional logic. In European Conference on Symbolic and Quantitative Approaches to Reasoning with Uncertainty, 347–358.Google Scholar
Condotta, J. F., Kaci, S. & Schwind, N. 2008. A framework for merging qualitative constraints networks. In International Florida Artificial Intelligence Research Society Conference, 586–591.Google Scholar
Darwiche, A. & Pearl, J. 1997. On the logic of iterated belief revision. Artificial Intelligence 89(1), 1–29.CrossRefGoogle Scholar
Delgrande, J. P. 2012. Revising beliefs on the basis of evidence. International Journal of Approximate Reasoning 53(3), 396–412.CrossRefGoogle Scholar
Dufour-Lussier, V., Hermann, A., Ber, F. L. & Lieber, J. 2014. Belief revision in the propositional closure of a qualitative algebra. In International Conference on Principles of Knowledge Representation and Reasoning.Google Scholar
Dufour-Lussier, V., Le Ber, F., Lieber, J. & Martin, L. 2012. Adapting spatial and temporal cases. In International Conference on Case-Based Reasoning, 77–91.Google Scholar
Egenhofer, M. J. & Mark, D. M. 1995. Naive geography. In International Conference on Spatial Information Theory, 1–15.Google Scholar
Fernyhough, J., Cohn, A. G. & Hogg, D. C. 2000. Constructing qualitative event models automatically from video input. Image and Vision Computing 18(2), 81–103.CrossRefGoogle Scholar
Grüne-Yanoff, T. & Hansson, S. O. 2009. From belief revision to preference change. In Preference Change: Approaches from Philosophy, Economics and Psychology, Grüne-Yanoff, T. & Hansson, S. O. (eds). Springer, 159–184.CrossRefGoogle Scholar
Hamilton, A. G. 1988. Logic for Mathematicians, 2nd edition. Cambridge University Press.Google Scholar
Hansson, S. O., Fermé, E. L., Cantwell, J. & Falappa, M. A. 2001. Credibility limited revision. Journal of Symbolic Logic 66(4), 1581–1596.CrossRefGoogle Scholar
Hue, J. & Westphal, M. 2012. Revising qualitative constraint networks: definition and implementation. In International Conference on Tools with Artificial Intelligence, 548–555.Google Scholar
Jin, Y. & Thielscher, M. 2007. Iterated belief revision, revised. Artificial Intelligence 171(1), 1–18.CrossRefGoogle Scholar
Katsuno, H. & Mendelzon, A. O. 1991. Propositional knowledge base revision and minimal change. Artificial Intelligence 52(3), 263–294.CrossRefGoogle Scholar
Konieczny, S., Marquis, P. & Schwind, N. 2011. Belief base rationalization for propositional merging. In International Joint Conference on Artificial Intelligence, 951–956.Google Scholar
Konieczny, S. & Pérez, R. P. 2000. A framework for iterated revision. Journal of Applied Non-Classical Logics 10(3–4), 339–367.CrossRefGoogle Scholar
Konieczny, S. & Pérez, R. P. 2002. Merging information under constraints: a logical framework. Journal of Logic and Computation 12(5), 773–808.CrossRefGoogle Scholar
Ligozat, G. & Renz, J. 2004. What is a qualitative calculus? a general framework. In Pacific Rim International Conference on Artificial Intelligence, 53–64.Google Scholar
Lin, J. 1996. Integration of weighted knowledge bases. Artificial Intelligence 83(2), 363–378.CrossRefGoogle Scholar
Lin, J. & Mendelzon, A. O. 1996. Merging databases under constraints. International Journal of Cooperative Information Systems 7, 55–76.CrossRefGoogle Scholar
Liu, J. & Daneshmend, L. K. 2004. Spatial Reasoning and Planning: Geometry, Mechanism, and Motion. Springer-Verlag.CrossRefGoogle Scholar
Ma, J., Liu, W. & Benferhat, S. 2015. A belief revision framework for revising epistemic states with partial epistemic states. International Journal of Approximate Reasoning 59(C), 20–40.CrossRefGoogle Scholar
Papini, O. 2001. Iterated Revision Operations Stemming from the History of an Agent’s Observations. Springer Netherlands, 279–301.Google Scholar
Pham, D. N., Thornton, J. & Sattar, A. 2006. Towards an efficient SAT encoding for temporal reasoning. In International Conference on Principles and Practice of Constraint Programming, 421–436.Google Scholar
Qi, G., Liu, W. & Bell, D. A. 2006. Merging stratified knowledge bases under constraints. National Conference on Artificial Intelligence, 281–286.Google Scholar
Randell, D. A., Cui, Z. & Cohn, A. G. 1992. A spatial logic based on regions and connection. In International Conference on Principles of Knowledge Representation and Reasoning, 165–176.Google Scholar
Randell, D. A., Galton, A., Fouad, S., Mehanna, H. & Landini, G. 2017. Mereotopological correction of segmentation errors in histological imaging. Journal of Imaging 3(4), 63.CrossRefGoogle Scholar
Revesz, P. Z. 1997. On the semantics of arbitration. International Journal of Algebra and Computation 7(2), 133–160.CrossRefGoogle Scholar
Sioutis, M., Alirezaie, M., Renoux, J. & Loutfi, A. 2017. Towards a synergy of qualitative spatio-temporal reasoning and smart environments for assisting the elderly at home. In IJCAI Workshop on Qualitative Reasoning, 901–907.Google Scholar
Spohn, W. 1988. Ordinal conditional functions: a dynamic theory of epistemic states. In Irvine Conference on Probability and Causation, 105–134.Google Scholar
Vilain, M. B. & Kautz, H. A. 1986. Constraint propagation algorithms for temporal reasoning. In AAAI Conference on Artificial Intelligence, 377–382.Google Scholar
Wallgrün, J. O. & Dylla, F. 2010. A relation-based merging operator for qualitative spatial data integration and conflict resolution, Technical report. Transregional Collaborative Research Center SFB/TR 8 Spatial Cognition.Google Scholar