Article contents
Is p-value 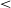 $<$ 0.05 enough? A study on the statistical evaluation of classifiers
$<$ 0.05 enough? A study on the statistical evaluation of classifiers
Published online by Cambridge University Press: 27 November 2020
Abstract
Statistical significance analysis, based on hypothesis tests, is a common approach for comparing classifiers. However, many studies oversimplify this analysis by simply checking the condition p-value < 0.05, ignoring important concepts such as the effect size and the statistical power of the test. This problem is so worrying that the American Statistical Association has taken a strong stand on the subject, noting that although the p-value is a useful statistical measure, it has been abusively used and misinterpreted. This work highlights problems caused by the misuse of hypothesis tests and shows how the effect size and the power of the test can provide important information for better decision-making. To investigate these issues, we perform empirical studies with different classifiers and 50 datasets, using the Student’s t-test and the Wilcoxon test to compare classifiers. The results show that an isolated p-value analysis can lead to wrong conclusions and that the evaluation of the effect size and the power of the test contributes to a more principled decision-making.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 5
- Cited by

