No CrossRef data available.
Article contents
A framework for belief revision under restrictions
Published online by Cambridge University Press: 12 September 2022
Abstract
Traditional belief revision usually considers generic logic formulas, whilst in practical applications some formulas might even be inappropriate for beliefs. For instance, the formula 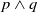 $p \wedge q$ is syntactically consistent and is also an acceptable belief when there are no restrictions, but it might become unacceptable under restrictions in some context. If we assume that p represents ‘manufacturing product A’ and q represents ‘manufacturing product B’, an example of such a context would be the knowledge that there are not enough resources to manufacture them both and, hence,
$p \wedge q$ is syntactically consistent and is also an acceptable belief when there are no restrictions, but it might become unacceptable under restrictions in some context. If we assume that p represents ‘manufacturing product A’ and q represents ‘manufacturing product B’, an example of such a context would be the knowledge that there are not enough resources to manufacture them both and, hence, 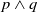 $p \wedge q$ would not be an acceptable belief. In this article, we propose a generic framework for belief revision under restrictions. We consider restrictions of either fixed or dynamic nature, and devise several postulates to characterize the behaviour of changing beliefs when new evidence emerges or the restriction changes. Moreover, we show that there is a representation theorem for each type of restriction. Finally, we discuss belief revision of qualitative spatio-temporal information under restrictions as an application of this new framework.
$p \wedge q$ would not be an acceptable belief. In this article, we propose a generic framework for belief revision under restrictions. We consider restrictions of either fixed or dynamic nature, and devise several postulates to characterize the behaviour of changing beliefs when new evidence emerges or the restriction changes. Moreover, we show that there is a representation theorem for each type of restriction. Finally, we discuss belief revision of qualitative spatio-temporal information under restrictions as an application of this new framework.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press


