1. Introduction
The 11B(p,α)2α fusion reaction shows great prospects in many fields. For example, p11B fusion is regarded as a neutron-free nuclear reaction and is a favorable candidate for fusion energy [Reference Rostoker, Binderbauer and Monkhorst1, Reference Kulcinski and Santarius2]. The cross section of the 11B(p,3α) provides a direct probe for structures in 12C [Reference Segel, Hanna and Allas3]. The study of the reaction can also give useful information to explain the astrophysical abundances of elements Li, Be, and B in young main-sequence F and G stars [Reference Boesgaard, Deliyannis and Steinhauer4]. Besides, the 11B(p,α)2α reaction provides a new method of cancer treatment [Reference Cirrone, Manti and Margarone5].
The 11B(p,α)2α nuclear fusion reaction was first studied in the 1930s by Oliphant and Rutherford [Reference Oliphant and Rutherford6]:
Shortly after, Dee and Gilbert [Reference Dee and Gilbert7] observed the breakdown of B into three particles with cloud track photographs. Then, the reaction has been studied numerous times to measure its cross-section [Reference Anderson, Dwarakanath, Schweitze and Nero8–Reference Becker, Rolfs and Trautvetter10]. Based on these experimental data, the empirical formula for the cross-sections is given by Nevins and Swain [Reference Nevins and Swain11]. In 2005, Belyaev et al. [Reference Belyaev, Matafonov and Vinogradov12] experimentally achieved the p11B fusion reaction by using an intense ps laser beam for the first time. Recently, experiments using laser-driven proton beams to initiate the p11B fusion reaction have demonstrated increasing α yields [Reference Labaune, Baccou, Yahia, Neuville and Rafelski13, Reference Belloni, Margarone, Picciotto, Schillaci and Giuffrida14], which has led to renewed interest in the scientific community for possible fusion energy applications.
In the laser-driven p11B fusion experiments, CR-39 type track detectors are used instead of silicon detectors like in usual nuclear physics experiments to detect ionizing particles [Reference Belyaev, Matafonov and Vinogradov12–Reference Belloni, Margarone, Picciotto, Schillaci and Giuffrida14]. CR-39 type track detectors are polyallyl-diglycol-carbonate (PADC) films composed of C12H18O7. The CR-39 type track detectors measure the absolute number of ions and are not sensitive to low fluxes of electrons and photons [Reference Jeong, Singh and Scullion15]. In preparation for an experiment with a laser-generated intense proton beam at the Laser Fusion Research Center at Mianyang to investigate the 11B(p,α)2α reaction, we performed an experiment to test the applicability of CR-39 type track detectors for cross-section measurement. We remeasured the cross-section of 11B(p,α)2α close to its first resonance and compared it to previous results.
Here, we report a measurement of the cross-section with a thick target and CR-39 type track detectors in the proton energy range of 140 keV–172 keV.
2. Experiment
The experiment was carried out at the 320 kV high-voltage platform at the Institute of Modern Physics in Lanzhou, mapping the energy region of the resonance at keV of proton energy Ep = 163. As shown in Figure 1(a), the proton beam passed through the magnetic quadrupole lens and the Faraday cup. It was then focused on the target with a focal spot diameter of about 1 mm. As shown in Figure 1(b), the incident energy of the proton beam was varied from 140 keV to 172 keV in steps of 4 keV, and the accuracy of the energy is
![]() . We used a thick target of natural boron, and the irradiation was carried out to irradiate the target from top to bottom, leaving a gap of 4 mm between each irradiation spot. The beam current was kept to about 1 μA. We aimed to have a total proton number on target 1015 and used a Faraday for monitoring. The arrangement was such that the proton beam was perpendicular to the target and parallel to the CR-39 track detector. The target is natural boron with a density of 2.35 ± 0.02 g/cm3, composed of 80.1% 11B and 19.9% 10B. The target has a thickness of 5.0 ± 0.1 mm with dimensions of 40 ± 1 mm × 44 ± 1 mm.
. We used a thick target of natural boron, and the irradiation was carried out to irradiate the target from top to bottom, leaving a gap of 4 mm between each irradiation spot. The beam current was kept to about 1 μA. We aimed to have a total proton number on target 1015 and used a Faraday for monitoring. The arrangement was such that the proton beam was perpendicular to the target and parallel to the CR-39 track detector. The target is natural boron with a density of 2.35 ± 0.02 g/cm3, composed of 80.1% 11B and 19.9% 10B. The target has a thickness of 5.0 ± 0.1 mm with dimensions of 40 ± 1 mm × 44 ± 1 mm.
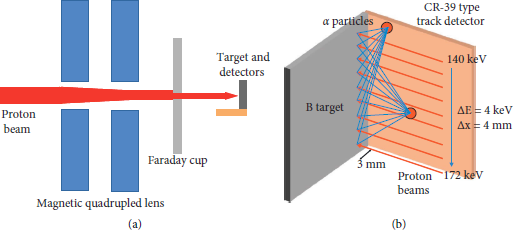
Figure 1: Experimental setup. (a) The proton beam passed through the magnetic quadrupled lens and the Faraday cup and then was focused onto (b) the target (grey) and CR-39 type track detector (orange-yellow). The proton energy scan was performed from 140 keV to 172 keV in steps of 4 keV near the Ep = 163 keV resonance, forming 9 spots with 4 mm intervals. The irradiation time for each energy is approximately 200 s, with a beam current of about 1 μA. The particles collected by any region (for example, the red circle) of the CR-39 track detector are the contribution of all nine incident proton beams.
The CR-39 type track detector, with a size of 50 ± 1 mm × 50 ± 1 mm × 1 ± 0.1 mm, was placed at 90° perpendicular to the target surface at a distance of 3 mm from the incident beam spot (Figure 1(b)). After irradiation, the CR-39 type track detector was chemically etched in a 6.0 mol/L NaOH solution and kept at a constant temperature of 80.0 ± 0.5°C for 1 h. Then the CR-39 type track detector was processed by washing, soaking, and drying to eliminate the interference of water droplets, stains, dust, etc. After this appropriate treatment, the tracks of α particles and protons with their respective diameters on the CR-39 type track detector were imaged and measured by an automatic track image analyzer. The measurement error of the track diameter does not exceed 0.05 um.
3. Results and Discussion
Both, α particles and scattered protons reach the CR-39 type track detector, therefore, it is necessary to tell them apart using the track diameters as a distinguishing feature. We measured α particle tracks on a CR-39 type track detector using a standard 241Am source emitting α particles at an energy of 5.49 MeV, as shown in Figure 2(a). The track diameters of α particles are near to 10 μm, which is consistent with the results of Hicks [Reference Hicks16], who etched the CR-39 type track detector with a solution of the same concentration and temperature as we did. According to Hicks’ result, the proton track diameters are smaller than α particle track diameters. Combining our results with Hicks’, we believe that there is a great difference in track diameter between protons and α particles, from Figure 2(b) it is obvious to distinguish the tracks with different diameters. Here, the elliptical tracks of protons are caused by the large angle of backscattering. As shown in Figure 1(b), the collected particles on the CR-39 type track detector arise from nine different incident spots. Therefore, particles directed to incident spots far away will have a large incident angle, which leads to the elliptical tracks.

Figure 2: Tracks on a CR-39 type track detector. (a) 5.49 MeV α particle tracks from a 241Am radioactive source after 3 h of etching. (b) Experimental particle tracks after 3 h of etching. (c) Experimental particle tracks after 1 h of etching. (d) Experimental particle tracks with the 5 um Al after 3 h of etching.
Figure 3 shows the number of detected particle tracks as a function of the track diameter with different etching times. The red line in the figure represents a double-gauss-curve fitting. For both etching times of 1 hour and 3 hours, there are two Gaussian peaks. The first peak is due to protons, and the second peak is caused by α particles.
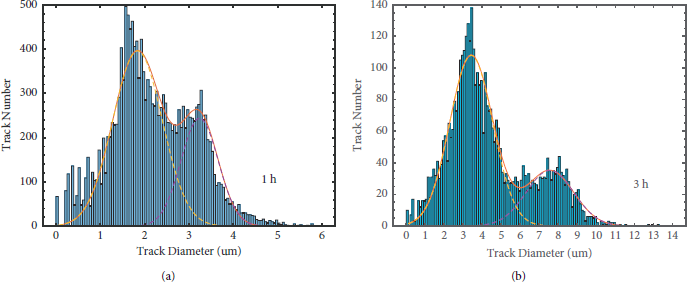
Figure 3: Statistical histogram of particle tracks after different etching times. (a) Particle tracks after 1 h of etching. (b) Particle tracks after 3 h of etching. The red line in the figure is the double-gauss-curve fitting for the track number as a function of its diameter.
Figure 2(b) and Figure 2(d) display the tracks without Al film and with 5 μm Al film after 3 h etching, respectively. We find that the number of tracks on a CR-39 type track detector with Al film is much less than that without Al film because most of the particles are protons and low-energy protons are filtered out by Al film, which is consistent with the results shown in Figure 3.
In addition, Figure 3 shows that when the etching time is 1 h, the proton track diameter and α track diameter overlap considerably; when the etching time is 3 h, the overlap area of the two tracks is small. This is due to the fact that the etching rates of proton and α particle tracks are different. As the etching time increases, the gap in track diameter will gradually increase. Therefore, it is more convincing to distinguish the two particle species with an etching time of more than 3 h.
However, there still remains some ambiguity because some particle tracks have a large range of mutual masking after an etching time of 3 hours. Therefore, we decided to calculate the yield based on an etching time of 1 hour.
As shown in Figure 3(a), because the proton track diameter and α track diameter overlap considerably, we finally choose the intersection of two Gaussian curves to distinguish two particle species. Thus, tracks with a diameter of more than 2.7 um are considered to be due to α particles. With this assumption, the relative systematic error is 7%.
As shown in Figure 1(b), for any region (for example, the red circle on the detector), on a CR-39 type track detector, the collected particles are the contribution of nine incident proton beams. We select nine regions on a CR-39 type track detector with uniform brightness and fewer bubbles near each spot, and then the equations are constructed as follows:
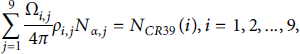
where N α,j is the α particle yield corresponding to the jth incident beam, N CR39(i) is the number of α particles detected on the i th CR-39 type track detector region, Ω ij is the solid angle of the j th proton beam to the i th CR-39 type track detector region. ρ ij represents the ratio of α particles that can escape from the target to the total amount of α particles that are produced.
In the thick target case, the change of reaction cross-section caused by proton energy deposition inside the target must be considered. The total reaction cross-section with the thick target is as follows [Reference Taulbjerg and Sigmund17]:
where n is the atomic density of the target, N (E) is the α particle yield per proton with the proton energy E, μ is the absorption coefficient of the target nucleus, θ is the angle between the normal direction of the target plane and the direction of the incident particle, φ is the angle between the normal direction of the target plane and the detector. The factor 1/3 corrects for the fact that for each reaction, three α particles are created.
In our experiment, the proton energy is 140 keV–172 keV, and the penetration depth into the boron target is about 1 um. The energy of α particles produced by p11B reaction is around 1 MeV and 4 MeV. According to the SRIM code and the α spectrum with the incident proton energy of 165 keV [Reference Becker, Rolfs and Trautvetter10], we can safely assume that almost all α particles pass through 1 um thick boron and reach the CR-39 type track detector. Thus, the second term in formula (3) can be ignored.
Figure 4(a) shows the α yield per proton for different energies of the incident proton beams, where the red line is the curve fitting the experimental data with a standard deviation of 24%. Figure 4(b) shows the cross section of p11B fusion, where the present data are obtained based on the formula (3) and the error of the cross-section was 28%. We can find that the resonance appears near 156 keV, and the measured resonance cross-section is 45.6 ± 12.5 mb. The position of the peak is slightly shifted to the left from the recognized resonance energy of 163 keV [Reference Oliphant and Rutherford6], and the value of the cross-section is consistent with the previous works [Reference Anderson, Dwarakanath, Schweitze and Nero8–Reference Becker, Rolfs and Trautvetter10, Reference Munch and Uldall Fynbo18].
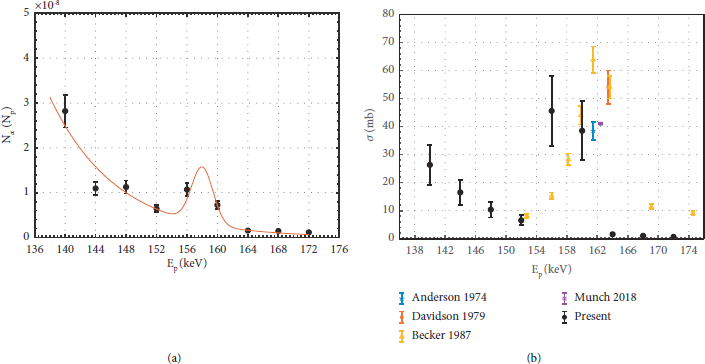
Figure 4: (a) The α yield per proton. The red line is the curve fitting. (b) p11B cross-section (the data are from References [Reference Anderson, Dwarakanath, Schweitze and Nero8–Reference Becker, Rolfs and Trautvetter10, Reference Munch and Uldall Fynbo18]). Here, we have corrected Becker’s value by multiplying a factor of 2/3.
The main errors are due to: (1) the fitting error of 24% in Figure 4(a); (2) the statistical error of 12% caused by particles counting on the CR-39 type track detector; and (3) the systematic error of 7%.
The higher values of the first four cross-sections result from proton backscattering. As shown in Figure 3(a), the proton track overlaps with the α particle track in a large range, so some protons will be mistaken for α particles during particle counting. In addition, the first proton beam may not be perpendicular to the target but at an angle to the target plane, which will cause large backscattering and a high particle count.
The shift of the resonance peak is mainly due to the very limited data near the resonance peak and the use of a thick target. According to Munch [Reference Munch and Uldall Fynbo18], the resonance width in the lab system of 163 keV is 5.76 keV, while the energy interval of proton beams in our experiments is 4 keV, which means that there are too few energy points measured near the resonance peak. Therefore, this causes a large error in the fitting of the peak position, thus leading to the shift of the peak.
When comparing all these cross-sections, we notice all values deviate significantly from the measurement of Becker et al. [Reference Becker, Rolfs and Trautvetter10]. We suspect that this is due to the normalization problem. Becker believes that a correction factor of 2 should be used when calculating the cross-section because two out of three α particles can be detected for one fusion reaction with detectors covering a large solid angle, while others divide the total α particle yields by a factor of 3. Considering our experiment, we have chosen several regions in the CR-39 type track detector to count the α particles. For the image shown in Figure 2, its size is 238.9 μm × 183.77 μm, and the solid angle of the image relative to the closest incident point is ΔΩ ≈ 10−4 rad. It is suggested that the α particles produced by
![]() reaction are isotropically in the center of mass system [Reference Becker, Rolfs and Trautvetter10], if the total α number produced in reaction is N
total, then the α number that can be collected in a region with a solid angle ΔΩ should be N
total × ΔΩ/4π. Considering that one reaction will produce three α particles, therefore, a factor of 3 should be divided when calculating the cross-section. In Figure 3(b) we have corrected Becker’s value by multiplying a factor 2/3.
reaction are isotropically in the center of mass system [Reference Becker, Rolfs and Trautvetter10], if the total α number produced in reaction is N
total, then the α number that can be collected in a region with a solid angle ΔΩ should be N
total × ΔΩ/4π. Considering that one reaction will produce three α particles, therefore, a factor of 3 should be divided when calculating the cross-section. In Figure 3(b) we have corrected Becker’s value by multiplying a factor 2/3.
4. Conclusion
In this experiment, the cross-section of the hydrogen-boron nuclear reaction at low energy is studied. The experiment was carried out on the 320 kV high-voltage platform, and the CR-39 type track detectors with high sensitivity to charged particles were used to record the particle yield. We can distinguish the protons and α particles clearly in CR-39 type track detector according to their track diameters, after etched in a 6.0 mol/L NaOH solution at a constant temperature of 80.0 ± 0.5°C for 3 hours. It is more effective to distinguish two particle species with an etching time of more than 3 h. For the nine incident proton beams, the particle yield is obtained by constructing 9-element equations. Based on the integral formula for thick target yield and the α particle energy spectrum, we obtain the peak value of the cross-section σ = 45.6 ± 12.5 mb near 156 keV. The peak value is consistent with previous results [Reference Anderson, Dwarakanath, Schweitze and Nero8–Reference Becker, Rolfs and Trautvetter10, Reference Munch and Uldall Fynbo18], and the position of the resonance is slightly shifted to the left. The shift of the resonance peak is mainly due to the very limited data near the resonance peak and the use of a thick target. Our results show the feasibility of measuring the reaction cross-section with CR-39 type track detectors in low-energy regions.
Data Availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Authors’ Contributions
Yongtao Zhao initiated and organized the experiments. Shizheng Zhang, Xing Xu, Yanhong Chen, Zhao Wang, Zexian Zhou, Lulin Shi, and Rui Cheng carried out the experiments together. Shizheng Zhang, Hao Xu, Zhigang Deng, Wei Qi, and Weimin Zhou etched and scanned CR-39 type track detectors. Wenqing Wei, Jieru Ren, Benzheng Chen, Bubo Ma, Zhongmin Hu, Fangfang Li, Lirong Liu, Mingzhe Yang, Zeyu Lai, Hongwei Yue, Jie Xiong, Zhongfeng Xu, Guanchao Zhao, Bing Liu, Di Luo, Yongtao Zhao, and Dieter H. H. Hoffmann contributed in the physical interpretation of experimental data. Shizheng Zhang, WenQing Wei, Jieru Ren, Yongtao Zhao, and Dieter Hoffmann drafted the paper and all the coauthors revised the manuscript critically. All the authors approved the final version to be published and agreed to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Acknowledgments
This experiment was performed at 320 kV high-voltage platform in Lanzhou. The authors are grateful to the staff of the Institute of Modern Physics. The work was supported by National Key R & D Program of China (No. 2019YFA0404900), Chinese Science Challenge Project no. TZ2016005, National Natural Science Foundation of China (Nos. U2030104, 12120101005, 12175174, and 11975174), China Postdoctoral Science Foundation (No. 2017M623145), State Key Laboratory Foundation of Laser Interaction with Matter (Nos. SKLLIM1807 and SKLLIM2106), and the Fundamental Research Funds for the Central Universities.





