1. Introduction
An emerging new scheme for a nuclear fusion microreactor that utilizes an ultra-intense laser pulse irradiating a fuel target consisting of a mixture of protons, borons, and potentially other additional fuels has been published recently by Ruhl and Korn [Reference Ruhl and Korn1]. In this concept, an ultrahigh-contrast, short-wavelength, short-pulse laser is used to irradiate a periodic arrangement of solid density nanowires with well-controlled diameter and pitch with an ensemble near-critical density. The nanowire array is made of boron and hydrogen in a 1 : 1 ratio. This target configuration allows for laser propagation into the bulk and continuous laser energy depletion. Upon propagation, the laser ionizes the nanowires fully, accelerates the released electrons to MeV energies, and expels them from the high-intensity region. The remaining positively charged ions of the nanowires undergo a Coulomb explosion, which accelerates the lighter protons to few-MeV energies. Upon colliding with the slower boron ions, pB-fusion reactions can be triggered that each generates three alpha particles via the reactions [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2]:
Further details of the reactor concept are outlined in Reference [Reference Ruhl and Korn1]. An experimental realization of this integrated fusion reactor concept poses unique challenges in many aspects, such as, for example, fulfilling the laser driver requirements, in target manufacturing, and to accurately diagnose the laser-target interaction under the demanding conditions inside the reactor. Most investigations about laser-driven proton-boron fusion have measured the escaping alpha particles [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2–Reference Baccou, Depierreux and Yahia11] to infer fusion efficiencies. However, alpha particle detection in such experiments is challenging due to the fact that the target also emits other ions such as protons and borons, with identical or similar energies and charge-to-mass ratios as the alpha particles, leading to overlapping signals in detectors. Being charged particles, the alphas are subject to electromagnetic fields that may surround the target, which can further complicate the analysis of the primary emission since the fields may accelerate or deflect the alphas [Reference Giuffrida, Belloni and Margarone5, Reference Picciotto, Margarone and Velyhan9]. Hence, additional diagnostic methodologies are needed to increase confidence in data interpretation. For example, measuring neutrons or activation products from secondary reactions is complementary to alpha particle detection and can lead to a better understanding of the physical processes occurring inside a fusion reactor.
The reactor design discussed above requires ordered nanowire arrays with very high aspect ratios made of boron and hydrogen. For our study, few-nm-diameter, unordered boron nitride (BN) nanowire nanotube (BNNT) targets that were developed by BNNT materials, LLC, were combined in a pitcher-catcher configuration [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2–Reference Bonvalet, Nicolai and Raffestin4, Reference Margarone, Morace and Bonvalet8, Reference Tayyab, Bagchi, Moorti and Chakera10, Reference Baccou, Depierreux and Yahia11] to experimentally measure the proton source decoupled from the fusion reaction. This combination enables the characterization and optimization of the proton beams and the dependence on laser and target parameters in pitcher-only experiments. Knowing the incoming proton beam parameters, secondary reactions such as those in Equations (1)–(3), but also neutron- or photon-generating reactions in a catcher target can be measured and compared to calculations using tabulated cross-sectional values [Reference Soppera, Bossant and Dupont12]. We include measured data from neutron time-of-flight, postshot nuclear activation, Thomson parabola ion spectrometer, and CR39 solid-state nuclear track detectors in our analysis. Nuclear activation results agree quantitatively and neutron signals qualitatively with the calculations, which ensure a reliable measurement of the primary particle distributions by this method. However, our analysis additionally highlights potential issues with such measurements if alpha particles are to be inferred.
2. Materials and Methods
The experiments were performed at the Advanced Laser for Extreme Photonics (ALEPH) at Colorado State University, Fort Collins, CO, USA [Reference Wang, Wang and Rockwood13]. ALEPH is a 0.85 PW, 45 fs Ti:Sapphire laser system operating at 800 nm wavelength. After compression, the pulse is converted to its second harmonic (400 nm) before it is directed to the target chamber. Five dichroic mirrors with >99.5 transmission at 800 nm are used to efficiently remove unconverted light yielding a contrast of >1012 up to ∼5 ps before the main pulse [Reference Curtis, Hollinger and Calvi14]. A dual-coated f/2 off-axis parabolic mirror is used to focus the laser pulse to a focal spot of about 1.5 μm full-width-at-half-maximum (FWHM). After second harmonic generation (SHG), the laser delivered 7 J on target, reaching a peak intensity of 5 × 1021 W/cm2. We have also performed experiments at the fundamental wavelength, bypassing the SHG crystal and dichroic mirrors. Here, the laser delivered 14.3 J on target. The temporal contrast was lower than for the SHG pulse due to an ASE prepulse of nanosecond duration with ∼10−8 intensity contrast. The stronger prepulse may result in reduced coupling to the nanostructured targets. However, the about twofold higher laser energy offsets the reduced coupling and leads to an overall higher proton yield as will be shown below.
2.1. Targets
For each measurement series, up to 30 shots were performed for statistics and to ensure the results are reproducible. The data were then averaged in postprocessing to yield single-shot results. We compared the efficiency of proton beam generation from 1.2-μm-thick Mylar foils (400 nm pulse), 7-μm aluminum foils (800 nm; thicker foil to reduce preheat of the rear side during the prepulse), and BN nanotube targets (both wavelengths). BN nanotubes have a similar tubular structure as carbon nanotubes in which carbon atoms are replaced entirely by boron and nitrogen atoms, arranged in a hexagonal lattice. The individual tubes are between 2 nm and 8 nm in diameter and can be several tens of microns long. The BN nanotubes formed a dense, unordered matrix (bucky paper sheets), wherein the tubes are randomly oriented and overlap to form thicker (several microns) clumps with voids in-between them. While the individual BN nanotubes have a near-solid density (∼2 g/cm³), the average density of the BN nanotube targets was 0.55 g/cm.
Figure 1(a) shows a sketch of the target chamber with the relevant diagnostics. The targets were continuous sheets of either thin foils or BN nanotubes. The sheets were sandwiched between two aluminum plates: one thicker plate to hold the samples on one side to which a 400-μm thin plate was bolted with 32 M2 screws to apply even pressure on the BN nanotube samples. An array of 3-mm-diameter holes in the plates spaced 8 mm apart in a 5 × 6 hole pattern enabled a shot series of up to 30 shots within one vent cycle. The inset in the bottom left corner shows a photograph of the target frame. The targets were mounted at the center of the chamber and irradiated by the s-polarized laser pulse at normal incidence. Figure 1(b) shows the pitcher-catcher configuration, where a 30-μm-thick BNNT target was irradiated by the 14.3 J, 800 nm pulse at normal incidence. A 1.5-mm (1/16 in.)-thick, commercially available BN ceramic plate in 400 μm distance was used as a catcher. The plate consists of 95% BN and about 5% B2O3. The natural boron used consists of 80% 11B and 20% 10B. A gap between the two targets was formed by using a second 400-μm plate identical to the one used on the BN nanotube target frame in direct contact with the pitcher and catcher plates. For each of the 30 targets, the hole in the plate resembled a cylindrical cavity with 3 mm diameter and 400 μm length. This configuration allowed us to place the catcher as close as possible to the source without interrupting the TNSA mechanism [Reference Brambrink, Schlegel and Malka15], but close enough to benefit from potential preheat by hot electrons or x-rays that lead to the generation of a hot, dense plasma in front of the catcher and potentially enhances the pB-fusion yield [Reference Labaune, Baccou and Depierreux3].
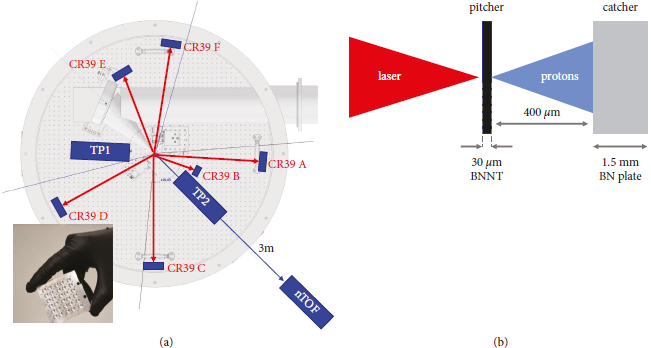
Figure 1: Experiment layout and target configuration. (a) shows a sketch of the target chamber with the relevant diagnostics. The laser pulse is focused by an f/2 off-axis parabolic mirror to an intensity of ∼5 × 1021 W/cm2 onto a target at the center of the chamber. Thomson parabola (TP) ion spectrometers are used to diagnose the generated proton beam. A filtered CR39 solid-state nuclear track detector is used to corroborate the TP measurements. A neutron time-of-flight (nTOF) detector is placed in about 3 m distance along the target normal direction. The inset in the lower-left corner shows a photograph of the target holder. (b) shows a sketch of the pitcher-catcher configuration. The laser pulse irradiates a 30-μm boron nitride nanotube target to create a proton beam (pitcher). The protons then irradiate a secondary boron nitride target (catcher) in 400 μm distance to trigger nuclear reactions.
2.2. Diagnostics
Two identical, compact Thomson parabola (TP) ion spectrometers are used to diagnose the accelerated ions. The TPs are custom-made by the facility with a design similar to Carroll et al. [Reference Carroll, Brummitt and Neely16]. The TPs were equipped with either Fuji MS or TR image plate to detect the parabolic ion traces. The image plates were scanned 20 min after the last shot on the target frame with a pixel size of 50 μm. The image plate data were converted to proton numbers using the calibration by Bonnet et al. [Reference Bonnet, Comet and Denis-Petit17]. Since the image plate digitizations were performed using a different scanner from the one used in [Reference Bonnet, Comet and Denis-Petit17], a 2 × 2 cm2 piece of filtered CR39 (Mi.am Srl, Piacenza, Italy) was placed next to the TP entrance at position “B” to corroborate the TP measurements and verify the calibration. Six different Al filters with 2, 15, 30, 45, 60, and 75 μm thicknesses were put in front of the CR39 to obtain information about the proton (and ion) energies hitting the CR39. The CR39 were etched for 30 minutes in 6.5 M NaOH solution at 70°C to reveal the ion tracks (“pits”). The pit diameter depends on not only the ion stopping power but also on the etch time. Longer etching is preferred for an increased accuracy of the track analysis (e.g., [Reference Baccou, Yahia and Depierreux18]). However, the ion flux for the thinnest filter was already close to saturation for most BN nanotube targets; therefore, the etch time had to be kept to a minimum. After etching, the images were digitized using a Keyence VHX-7000 digital microscope equipped with a 12.2 megapixel VHX-7100 image acquisition unit. The microscope resolution was determined with a high-resolution microscopy USAF test chart (Edmund Optics) to be 2400 lp/mm, which is sufficient to detect the ∼0.5-μm-diameter proton pits. After digitization, the pits were registered using a custom MATLAB routine.
To measure neutrons from (p, n) or (α, n) fusion reactions in either target, an EJ-228 plastic scintillator-photomultiplier tube (PMT; Hamamatsu H2431-50) time-of-flight detector was placed in 3 m distance from the target location along the laser axis. The detector was enclosed in a housing made of 5-cm-thick lead bricks to reduce the high-energy photon signal reaching the PMT. The detector was calibrated previously [Reference Curtis, Hollinger and Calvi14, Reference Curtis, Calvi and Tinsley19]. However, due to the strong photon signal generated during the experiments with 800 nm wavelength, the PMT bias voltage had to be reduced significantly to avoid saturation of the trace, which negated the calibration.
2.3. Nuclear Reactions Creating Neutrons and/or Positron Emitters
In addition to the on-shot diagnostics, two Scionix Holland 51B51/2M-E1 gamma spectrometers equipped with a 51-mm-diameter, 51-mm-long NaI (Tl) scintillator, coupled to a CAEN DT5725S digitizer, were used to measure the activation of the target remnants after the shots. An integration time of 5 minutes was chosen to provide sufficient counts at later times. This setup enabled us to measure the gamma spectrum of the samples vs. time, not just the activation [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2], to verify that the measured signal is from positron emitters and not from other decay channels such as, for example, excited nuclei from Bremsstrahlung photoexcitation.
In the pitcher-catcher experiment, the accelerated protons can create a multitude of nuclear reactions [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2, Reference Bonvalet, Nicolai and Raffestin4]. Table 1 lists some of the possible (p, x) and (α, x) reactions that create a neutron or a positron emitter as reaction products. Some of the reactions have a negative Q value of a few MeV, meaning the incident projectile needs to overcome a threshold energy to trigger the reaction. The second column in the table lists approximate values of the reaction cross section near the peaks for a quick judgment of the likelihood of the reaction. The analysis discussed below uses the tabulated values that were obtained with the Java-based nuclear information software (JANIS) [Reference Soppera, Bossant and Dupont12] across multiple databases. The third column lists the half-life of the generated positron emitters. The most probable activation product is
![]() with a half-life of about 20 minutes. For early times, the activation may have a contribution of
with a half-life of about 20 minutes. For early times, the activation may have a contribution of
![]() , and for late times, the measurements may detect the presence of
, and for late times, the measurements may detect the presence of
![]() that has a half-life of about 2 hours.
that has a half-life of about 2 hours.
Table 1: Nuclear reactions creating neutrons and/or positron emitters in boron, nitrogen, and oxygen.
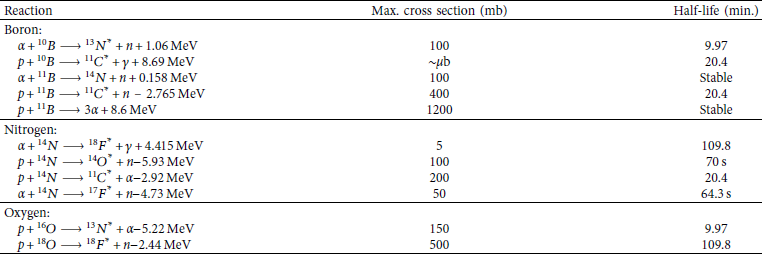
The primary alpha-generating fusion reaction is listed for comparison (see Equations (1)–(3)). The reactions are used in the analysis to infer primary proton and alpha yields. The cross-sectional values quoted are approximate values near the peaks for a quick judgment; the analysis uses the tabulated values. The half-life of the created positron emitters is given in minutes, unless otherwise quoted.
The
![]() isotope was used in [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2] to infer the presence of alpha particles in a BN catcher via the reaction
isotope was used in [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2] to infer the presence of alpha particles in a BN catcher via the reaction
However, there are two potential issues with this inference. One issue is the rather low cross-sectional value of only 5 mb. This low value ruled out this alpha particle detection path in an earlier work looking at nuclear reaction diagnostics for magnetic fusion devices [Reference Cecil, Medley, Nieschmidt and Zweben20]. The other issue is that
![]() can also be produced when the target contains oxygen impurities via
can also be produced when the target contains oxygen impurities via
The stable 18
O isotope has an abundance of about 0.2% in natural oxygen. The 18
O (p, n)18
F reaction has a high cross section of ∼500 mb at 5 MeV [Reference Takács, Tarkanyi, Hermanne and Paviotti de Corcuera21, Reference Hess, Takacs, Scholten, Tarkanyi, Coenen and Qaim22]. Since this reaction is triggered by the primary protons and not by alphas, if
![]() is detected in the experiment a precise knowledge of the oxygen contamination and the incoming proton spectrum are required to infer the relative contributions of proton and alpha particles to the
is detected in the experiment a precise knowledge of the oxygen contamination and the incoming proton spectrum are required to infer the relative contributions of proton and alpha particles to the
![]() generation.
generation.
3. Results and Discussion
3.1. Proton Spectra for 2ω Irradiation, Pitcher-Only
Starting with 2ω irradiation, Figure 2 compares proton spectra measured with TP1 and TP2 for a 1.2-μm-thick Mylar foil compared to a BN nanotube target. The BN nanotube target was 110 μm thick and had an average density of 0.55 g/cm³, which is 2–3 times lower than solid density. The plots show the proton spectra for a single shot, normalized to 1 J of laser energy.
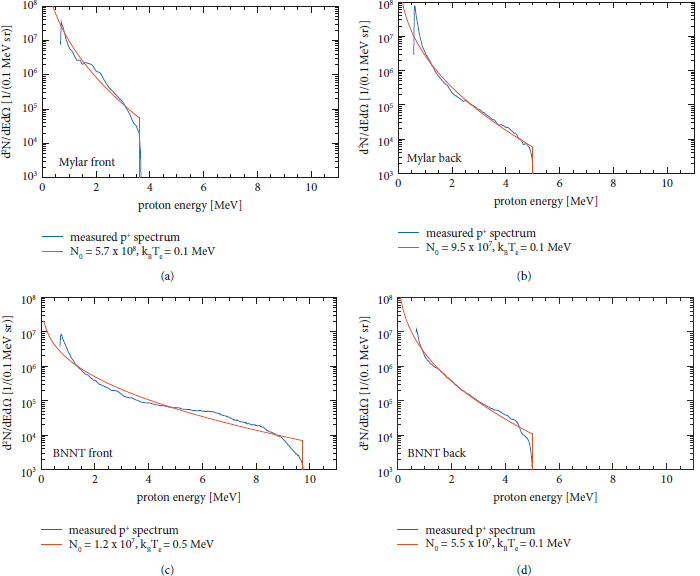
Figure 2: Proton spectra for 2ω irradiation, Mylar foil vs. BN nanotube target. The proton spectra from front (a) and back side (b) of the 1.2-μm Mylar foil are nearly identical indicating TNSA on both sides of the target. The 100-μm-thick BN nanotube target results in more than double the maximum energy on the front side (c) and still ∼5 MeV from the rear side (d), suggesting that the laser is absorbed more efficiently due to the nanostructure of the BN nanotubes.
Figures 2(a) and 2(b) show the Mylar foil proton spectra at the front (laser irradiated) and back side, respectively. The spectra look nearly identical, confirming the high contrast of the laser pulse that leads to TNSA proton acceleration on both sides of the target [Reference Ceccotti, Levy and Popescu23]. The maximum proton energies are 4–5 MeV. The spectral shape can be described by
where N 0 and k B T e are the fit parameters (orange lines). Except for Figure 2(c), N 0 ≈ 108 and k B T e ≈ 0.1 MeV. Using the filtered CR39 plates (positions A thru F), we confirm that the proton emission is strongly peaked in the target normal directions, as expected.
Figures 2(c) and 2(d) show the proton spectra for the 110-μm-thick BN nanotube target. Of striking difference is the front side proton spectrum, which reaches almost 10 MeV. Here, N 0 ≈ 107 and k B T e ≈ 0.5 MeV. The rear side spectrum is similar to the Mylar foil, even though the BN nanotube is 100 times thicker than the Mylar foil. The filtered CR39s measured about 100 times more particles along the target normal directions, as well as significant particle counts in all the measured off-normal directions. We interpret these findings as due to enhanced, volumetric absorption of the laser pulse compared to surface absorption for the foil target due to both the nanostructured surface and the overall reduced density.
3.2. Proton Spectra for 2ω vs. 1ω Irradiation, Pitcher-Only
After verifying that BN nanotubes lead to hotter proton spectra at high-contrast, 400-nm irradiation, we repeated a similar measurement using the fundamental wavelength and with higher laser energy. Figure 3(a) shows a direct comparison of Mylar foil and BN nanotube target backside proton spectra for 2ω irradiation, and Figure 3(b) the same for 1ω, for 30-μm BNNTs, and for a 7-μm Al foil. The spectra were measured by integrating over 10 shots (2ω, 20 shots for 1ω) for reproducibility. The plots show the processed proton spectra for a single shot, normalized to 1 J of laser energy.
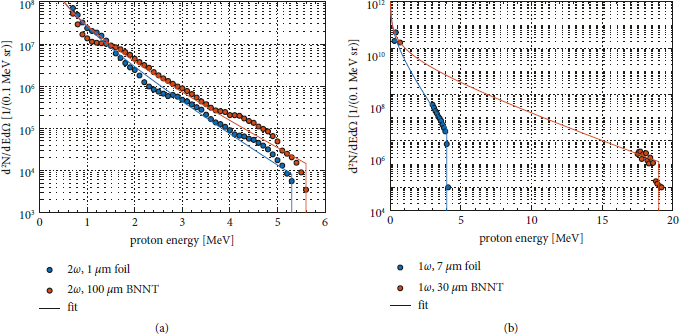
Figure 3: Rear-side TP ion spectra (TNSA protons) show 104 times more particles for 1ω vs. 2ω irradiation. The data show single-shot spectra, per 1 J of laser energy, by dividing the multishot integrated measurement by the number of shots and laser energy. (a) The 2ω spectra are very similar for both the Mylar foil and the BN nanotube target, despite the BN nanotube target being 100 times thicker. (b) The 1ω spectra exhibit about 100 times more protons at 1 MeV. Additionally, the BN nanotube target accelerated protons up to 20 MeV energy, about five times higher than the Al foil target.
The 2ω spectra are very similar for both the foil and the BN nanotube targets, despite the BN nanotube target being 100 times thicker. Compared to 2ω irradiation, the 1ω spectra exhibit about 100 times more protons at 1 MeV. Additionally, the BN nanotube target accelerated protons up to 20 MeV energy, about five times higher than the Al foil target. This finding supports the hypothesis that thinner BN nanotube targets outperform comparable foil targets as a proton source. The hundredfold higher particle numbers were not expected; as a result, the TP traces for the 1ω shots are saturated over large parts of the parabolic traces. The saturated parts were removed from the analysis and the spectrum was analyzed near the high and low energy ends of the trace where the dispersion in the TP was large enough to reduce the particle flux below saturation (low energies) or the particle numbers were low enough (high energies).
After plotting the extracted particle numbers from the TP traces, we fitted spectra using Equation (6) to determine the particle yields and slope.
For the 7-μm Al foil irradiated at 1ω, we compared the particle flux detected with CR39 #B and the TP trace. The particle count in this CR39 detector reached about 5 × 108 protons/sr/J/shot behind the 75-μm Al filter, corresponding to protons with energies above 1.6 MeV. This filter thickness ensures that only protons were detected in the CR39. Alpha particles need ∼12 MeV and carbon or B, N ions need >60 MeV to penetrate the filter. The pit diameters behind this filter are all about 500 nm, in line with the expected proton pit diameters for our etch conditions. Integrating the TP spectrum for energies above 1.6 MeV results in a proton count of 3 × 108 protons/sr/J/shot, giving confidence in our TP calibration. For comparison, the BN nanotube created about ten times more protons.
We did not field an imaging proton spectrometer such as, for example, a stack of radiochromic films [Reference Nurnberg, Schollmeier and Brambrink24, Reference Schollmeier, Geissel, Sefkow and Flippo25] to measure the full beam size or divergence angle. However, typically TNSA beams exhibit a cone angle of up to ±15° [Reference Nurnberg, Schollmeier and Brambrink24–Reference Prencipe, Metzkes-Ng and Pazzaglia28] for the lower energies, which contribute the most to the particle numbers. Assuming this value as an estimate for the proton beam divergence for both target types results in 4 × 109 protons per shot for the Al foil and 4 × 1010 protons for the BN nanotube target. These yields are similar to the results from [Reference Prencipe, Metzkes-Ng and Pazzaglia28], who compared proton beam from thin foils to foam-coated thin foils. There, the foam-coating resulted in enhanced laser absorption and about four times higher proton yield than uncoated foils. Our results indicate that BN nanotube targets could yield even better absorption and more protons, potentially due to the nanostructures spanning the entire material. Even higher proton energies are expected from thinner BN nanotube targets [Reference Fuchs, Antici and d’Humieres29, Reference Schreiber, Bolton and Parodi30], but this was beyond the scope of this investigation.
3.3. Pitcher-Catcher Experiment at 1ω Irradiation
After having determined that BN nanotube targets irradiated at 1ω created the proton source with the highest particle numbers and energies, a pitcher-catcher experiment was performed where the proton beam was directed at a BN plate as described in Figure 1(b). The most striking results were that we measured significant nuclear activation during the postshot gamma spectroscopy, as well as a neutron time-of-flight signal, both of which are clear evidence for nuclear reactions.
3.4. Nuclear Activation
An example measurement is shown in Figure 4. The gamma spectrum is dominated by the 511 keV electron-positron annihilation peak, verifying the existence of positron emitters (in contrast to, e.g., excited nuclei from Bremsstrahlung photoexcitation). The second peak at about 250 keV is from backscattered 511 keV primary photons in the lead shielding nearby. The decay of the 511 keV peak was monitored in 5-minute integration intervals until it reached background levels. Prior to the measurements, the background counts were determined using the same integration time. Two gamma spectrometers on either side of the target frame were used in ∼1 cm distance to monitor an almost 4π solid angle. The detection efficiency of the NaI scintillator for 511 keV photons was estimated as 35% [Reference Cecil, Medley, Nieschmidt and Zweben20].
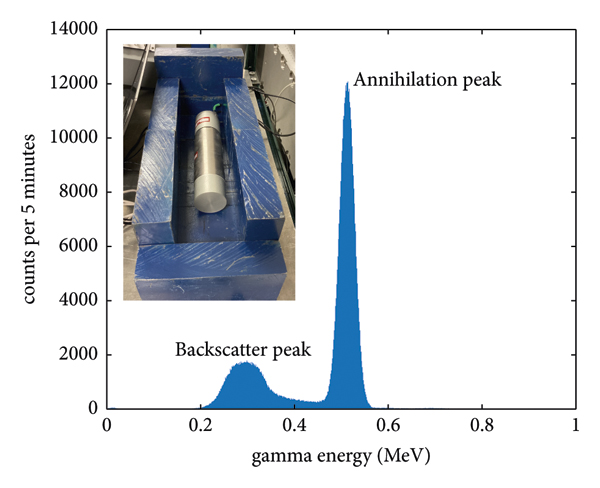
Figure 4: Postshot gamma spectroscopy of the pitcher-catcher shots. A strong peak at 511 keV is measured, verifying the existence of positron emitters (in contrast to, e.g., excited nuclei from photoexcitation). The second peak at about 250 keV is from backscattered 511 keV primary photons in the lead shielding nearby. The photograph in the inset shows one of the detectors inside of the lead housing with the top removed.
The activation results for the pitcher-catcher shots are plotted in Figure 5. The pitcher-only shots performed earlier did not produce any measurable activation above the background. Therefore, we can assume that the majority of the measured activation is from the BN catcher plate and not the primary source target. As discussed above and shown in Table 1, the most likely isotopes to be created are 11 C, 13 N, and 18 F. The three decays were fitted to the measured data to obtain the partial contributions of each nuclide. The decay curves can be extrapolated to t 0 when the last laser shot occurred to get the activity A right after the shots. The total activity A total was 11.5 kBq after 30 shots. From the activity and the decay constant λ = ln (2)/τ, where τ is the half-life, the number of activated nuclei can be easily calculated as N = A/λ.
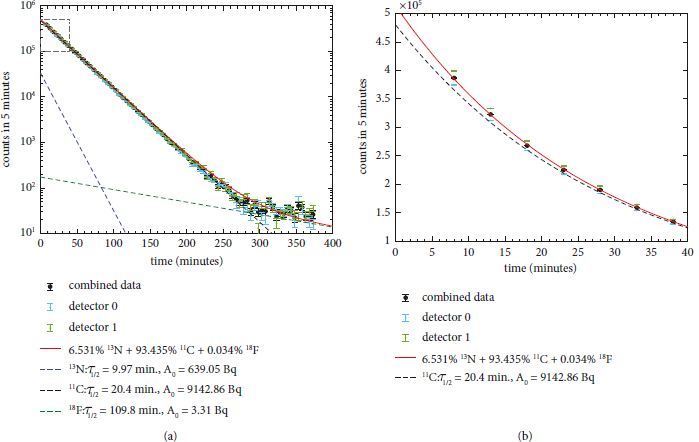
Figure 5: Pitcher-catcher nuclear activation measurements. (a) Each black data point shows the background-corrected counts as an average of the two spectrometer counts (shown in light-blue and light-green). Time zero corresponds to the time of the last laser shot on the targets. The dashed lines are the result of fitting the decays of 13 N, 11 C, and 18 F to the data. Note the logarithmic ordinate. Details are given in the figure legend and the text. (b) is a zoomed view of the data at early times, on a linear scale, to better visualize that the ∼6.5% contribution of 13 N is needed to match the measurements.
The fit results are summarized in Table 2 and plotted with the dashed lines in Figure 5. The most abundant isotope is 11 C, which is from protons fusing with 11 B to create the 11 C isotope and a neutron.
Table 2: Activation results for the pitcher-catcher shots after 30-shot integration.
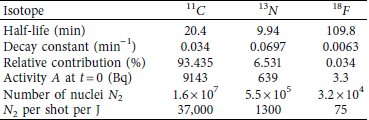
Each column lists physical and fit parameters for the three discussed nuclei. N 2 is the calculated number of nuclei based on the measured activity A. The last row is the same number, normalized per shot per 1 J of energy.
It is worthwhile to compare our results to earlier measurements by Labaune et al. [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2]. In [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2], the laser energy was about 10 J. Up to 500 Bq of nuclear activation was detected. Our laser delivered 14.3 J and created ∼400 Bq per shot, which is similarly efficient but does not require a secondary laser pulse to boost the activation levels. Unlike [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2], we see a clear contribution of 13 N to the measurements as shown in the zoomed view in Figure 5(b). At late times, 18 F appears with an activity of 3 Bq, about the same activity as measured in [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2]. However, the relative contributions of the three different isotopes are very different. In [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2], the 18 F isotope had a relative abundance of 0.6%, whereas our measurements yield an about 20x lower contribution. Reference [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2] interpreted the 18 F creation to be originated by alpha particles and a proof-of-concept that secondary reactions are possible. If that is true, the alpha particles should also create 13 N isotopes. The measurements in [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2] showed hints of 13 N creation but were not conclusive.
Our measurements show a clear evidence for 13 N isotopes, as well as 18 F. In the following, we calculate the expected number of isotopes assuming beam-target fusion reactions and using the 1ω BN nanotube target spectrum from Figure 3 as input. The number of reaction products N 2 depends on the number of incoming projectiles N projectile, target ion density n target, cross section σ, and projectile range R:
The projectile range R depends on the incoming projectile energy E 0 and the ion-stopping power dE/dx. As the projectile slows down in the material, its energy is reduced and correspondingly the cross section changes. Therefore, the product σ R in Equation (7) is replaced by an integral over the cross section and stopping power to calculate N 2 [Reference Giuffrida, Belloni and Margarone5]:
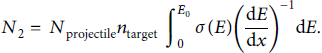
The stopping power was taken from the SRIM software package [Reference Ziegler, Biersack and Ziegler31], and the cross-sectional data were obtained via the Janis database [Reference Soppera, Bossant and Dupont12]. Taking the proton-boron fusion reaction 11 B (p, α) 2α as an example, with the analytic cross section from [Reference Nevins and Swain32], an incoming proton energy of E 0 = 1 MeV, and noting that this reaction creates three alpha particles per proton, we calculate a yield of 3.9 × 10−5 alpha particles per proton. The slight discrepancy to the efficiency obtained in [Reference Giuffrida, Belloni and Margarone5] results from the different density of the BN plate used in our work.
Next, we integrate Equation (8) over the 1ω BN nanotube proton spectrum to calculate the total number of activated nuclei. Here, the energy intervals for integration are between the threshold energy of the reaction (for negative Q values, zero elsewhere) and the 19 MeV maximum energy.
The results are summarized in Table 3. The first column shows the calculated alpha particle yield, which is 6 × 106 per shot per J. The second column shows that the calculated 11 C yield matches the measured one fairly closely. The difference could be due to the assumption of ±15° cone angle, which overestimates the proton yield for higher energies. Additionally, the catcher target featured some shallow ablation craters after the shot, which may have reduced the target activation due to some missing material.
Table 3: Reaction product yields per primary projectile in BN and expected yields for the BN nanotube 1ω spectrum.

The ion densities are calculated assuming the BN plate (density of 2.1 g/cm3) contains ∼95% BN and ∼5% oxygen contamination. The natural boron consists of 80%11 B and 20%10 B. Of the natural oxygen, the 18 O isotope is about 0.2% abundant. N 2 is given per shot per J of laser energy.
The third column compares the calculated and measured 13 N generation. In pure BN, 13 N can be generated by alpha particles [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2], but since our target had significant oxygen contamination, there is also a very probable proton-induced reaction channel. Assuming that all alpha particles generated by the primary p-11 B reaction (column 1) have energies between 1 and 5 MeV and are all stopped in the BN, the most optimistic calculation results in less than one 13 N nucleus being created per J. However, our measurement indicates that about 1300 nuclei/J are created. The calculated 13 N yield per alpha particle is ∼8 × 10−8. If we attribute all the measured 13 N nuclei as being created by alpha particles, this results in ∼2 × 1010 alpha particles per shot per J. Performing the same estimate for the 18 F yield (using a constant σ = 5 mb due to the lack of detailed cross-sectional data) results in a 18 F yield per alpha particle of 1.8 × 10−7, translating into ∼4 × 108 alphas per shot per J. The two calculated alpha yields are inconsistent with each other by a factor of 50. The estimate from 13 N is also within a factor of two of the measured proton yield, which appears too high given the low fusion probability due to beam-target interaction.
Performing the 13 N calculation under the assumption of the proton-oxygen reaction results in a similar number as the measured one. The same comparison holds true for 18 F generation.
Therefore, we conclude that for our pitcher-catcher experiment, the majority of the measured radioactive isotopes are the result of protons interacting with 11 B or oxygen contamination. However, some discrepancies still prevail between the calculated and measured data. In particular, the calculated 11 C number is higher while the calculated 13 N is lower than measured, leaving room for potentially higher alpha numbers than calculated here.
3.5. Neutron Spectra
The data of the previous section show that the majority of the activation is from 11 B (p, n)11 C, which creates a neutron with each created 11 C nucleus. For 14 J laser energy, this should create about 106–107 neutrons per laser shot. This neutron yield is detectable at ALEPH as shown in earlier works [Reference Curtis, Hollinger and Calvi14, Reference Curtis, Calvi and Tinsley19]. Figure 6(a) shows the neutron time-of-flight trace for the pitcher-catcher shots compared to shots using an Al pitcher only. The traces were averaged for 30 shots. The initial high-energy photon flash was very intense in all of the shots and created a temporary saturation of the traces followed by an exponential decay. Nonetheless, we have observed modulations of the traces during the decay of the scintillator for our pitcher-catcher shots with BN nanotube targets that were not present when the Al targets were used. To find out whether these modulations correspond to neutrons, and for a better comparison between the reference and pitcher-catcher shots, a multi-exponential function with constant offset was fitted to the decay curves and subtracted from the data to reveal a neutron signal. The fast rise time of the photon flash indicates the arrival time of the laser pulse on target, which was correspondingly used to calculate the neutron time-of-flight. Even with background subtraction, the data exhibit high-frequency noise and a poor signal-to-noise ratio due to the presence of a strong electromagnetic pulse. Using the noise amplitude of the Al data, for which we do not expect to measure any neutrons, we defined a baseline noise level of ±0.35 V (marked by the shaded area in Figure 6(a)). The amplitude of the pitcher-catcher signal at delay times between approximately 100 to 150 ns is significantly stronger than this noise level, suggesting it may be from neutrons.
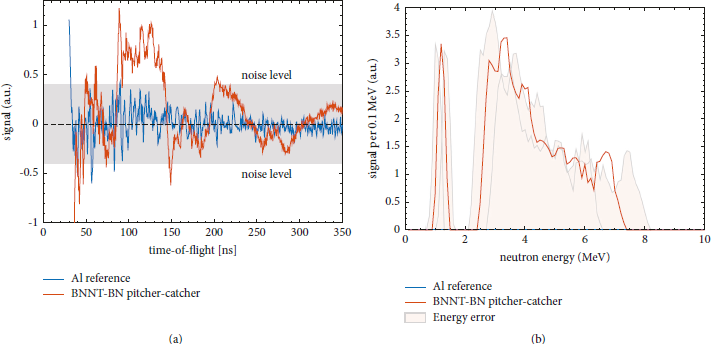
Figure 6: Neutron time-of-flight data and spectra, from an average of 30 shots. (a) shows the background-corrected traces for the pitcher-catcher experiment vs. a pitcher-only aluminum target. The pitcher-catcher trace shows a signal at around 100 ns that is above the noise level. (b) shows the same data, converted to neutron kinetic energy. The first peak corresponds to ∼2–7 MeV energy, and a potential second peak is at ∼1.3 MeV energy. It is at present not clear whether this second peak is an artifact due to the noise; we have planned to investigate this in the future. The uncertainty in the detector distance leads to an error of the calculated energies, visualized by the shaded areas.
To generate a neutron spectrum, we disregard data that fall within the noise level by setting these values to zero. The time-of-flight data were converted to neutron kinetic energies and then sorted into a histogram with 0.1 MeV step size. We assume a constant detector response for the conversion from TOF into the spectrum. Since we had to change the bias voltage of the PMT to a level beyond our calibration, we cannot convert the PMT response to a neutron flux. In addition to that, the neutron signal occurred during the decay of the scintillator due to the strong gamma flash. The instrument response vs. neutron flux in this operating mode is not known. Therefore, the spectrum is given in “signal-per-0.1-MeV” units, which will only allow for qualitative but not for quantitative comparisons to our calculations.
The resulting spectrum corresponds to neutrons between 2 and 7 MeV, with an error of ±0.5 MeV due to uncertainties in the detector distance. The spectrum decays toward higher neutron energy. The irregular shape of the spectrum is partly due to the high-frequency noise mentioned above and partly due to the low neutron statistics (for ∼106 neutrons emitted into 4π, about 10 neutrons per shot are hitting the detector). We also observe a single peak at about 1.3 MeV from the signal at ∼200 ns that is above the noise level. It is at present not clear whether this is an artifact due to the noise; we have planned to investigate this in the future.
To aid in the interpretation of the neutron data, we modeled an expected neutron spectrum using the 1ω BN nanotube proton spectrum as an input, together with the cross sections for (p, n) and (α, n) reactions from Table 1. The neutron spectra were generated using a custom Monte Carlo code to generate an exponentially decaying population of 106 protons that resembled the measured spectrum, times a multiplicative factor to account for the actual number of protons. A second, Gaussian spectrum that is centered at 3 MeV with a FWHM of 1 MeV was used to simulate an assumed population of 106 alpha particles, again times a multiplicative factor to correct for the actual number. For each population, the energy-dependent probability of creating a neutron was calculated via interpolation of the cross-sectional data tables. The neutron energy was determined by the nuclear reaction kinematics for binary collisions where the neutron is generated in the forward direction. The resulting neutron population was then converted to a histogram to generate the spectrum. The total number of neutrons was weighted by the primary particle numbers to calculate the relative neutron yields from protons and alpha particles. Figure 7(a) shows plots of the initial particle distributions (grey and black lines), plus the cross sections of the neutron-producing reactions. The alpha particle yield was assumed to be dominated by the number of 1 MeV protons, indicated by the blue circle.
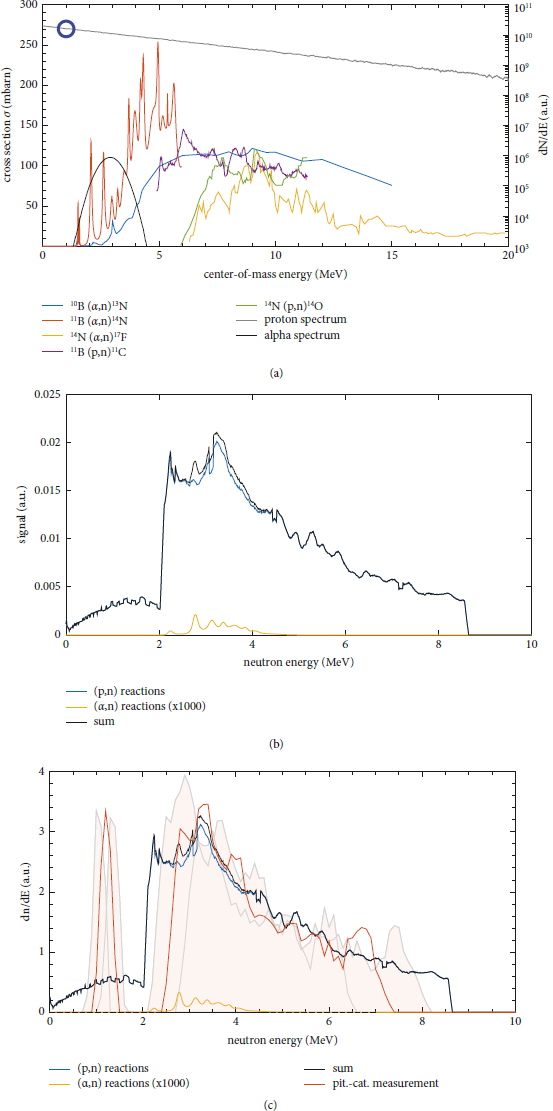
Figure 7: Calculated vs. measured neutron spectra. (a) The cross-sectional data for neutron-producing reactions in BN show that multiple reaction channels for (p, n) and (α,n) exist with relatively high cross sections. The grey and black curves are plots of the p and α distributions used to generate the artificial neutron spectra shown in (b). Note that the alpha-generated neutron spectrum was multiplied by a factor of 1000 for visualization purposes; otherwise, its contribution to the total spectrum would not be visible. The comparison between the calculated and measured spectra shown in (c) shows that it is plausible that the measured neutrons originate from (p, n) reactions, showing its diagnostic potential. An (α, n) contribution to the measurement would fall into the same energy range. A potential (α, n) contribution cannot be resolved with the current measurement sensitivity.
Figure 7(b) shows the calculated neutron spectrum and its relative contributions from protons and alpha particles. Note that the alpha spectrum had to be multiplied by 1000 to become visible. This plot shows that the expected neutron energies from both kinds of projectiles overlap in their energies, and that for beam-target interactions as assumed here the neutron yield from protons far outweighs the neutron yields from alphas. Due to the interplay between the threshold energy to trigger the reaction and its cross sections, the spectrum is dominated by the 14 N (p, n)14 O reaction for energies below 2 MeV. Above that, the neutron spectrum is dominated by 11 B (p, n)11 C reactions. The proton-neutron spectrum decays toward higher energies due to the exponential proton spectrum.
Since we assume a Gaussian alpha particle spectrum centered at 3 MeV, the resulting alpha-neutron spectrum is shifted to about 4 MeV due to the reaction kinematics. The alpha-neutron energies are roughly centered in-between the proton-neutron energies. Overall, the neutron spectrum is dominated by (p, n) reactions in our experiments.
Figure 7(c) qualitatively compares the calculated neutron spectrum to the measured nTOF spectrum. The measured energies and slope are fairly well reproduced; however, the measured spectrum appears to fall into a narrower energy range. This may be due to an insufficient background correction of the measured data for reasons mentioned above, as well as due to the low particle statistics that result in near single events at the scintillator.
4. Summary and Conclusions
The measurements and results discussed in this study demonstrate that BN nanotube targets are a significantly more efficient proton source than regular foils, potentially better than previously published nanostructured targets [Reference Margarone, Klimo and Kim7, Reference Prencipe, Metzkes-Ng and Pazzaglia28]. This warrants further investigations into their use as efficient proton sources for applications.
The strongest proton beams were created by irradiating a BN nanotube target with a 1ω pulse resulting in a yield of 6 × 108 protons/sr/J/shot. Assuming a cone angle of ±15° [Reference Nurnberg, Schollmeier and Brambrink24–Reference Prencipe, Metzkes-Ng and Pazzaglia28], this results in 4 × 1010 protons/J/shot. When this proton beam was directed to a BN catcher target, it created nuclear activation with more than 10 kBq, as well as a measurable neutron signal. Our analysis showed that the nuclear activation was mainly due to 11 B (p, n) 11 C reactions, with small contributions from 13 N and 18 F. Using tabulated nuclear reaction cross-sectional values and the input proton spectrum measured without the catcher, we were able to reproduce the quantity of activated nuclei within a factor of two. Through these calculations, we infer a theoretically calculated alpha particle yield due to proton-boron beam-target interaction of 6 × 106/J. This is comparable to similar pitcher-catcher experiments published in [Reference Labaune, Baccou and Depierreux3], but without an additional heating laser.
Comparing our nuclear activation measurements with calculations of the expected yields due to the incoming proton spectrum, we show that the 13 N and 18 F nuclei created in our BN sample are most likely due to protons activating oxygen contamination inside the bulk material and less likely due to alpha particles creating secondary reactions. In fact, attributing all of the measured 13 N nuclei to being generated by alpha particles via 10 B (α, n) 13 N, and 18 F nuclei via 14 N (α, γ)18 F as suggested in [Reference Labaune, Baccou, Yahia, Neuville and Rafelski2] would, in our case, result in alpha yields that are not only inconsistent with each other but also within a factor of two of the measured primary proton yield, which appears too high given the expected low yields of beam-target fusion reactions. However, more careful examination shows that our calculated 11 C count due to proton reactions is higher than measured while the calculated 13 N count due to proton reactions is lower than measured, which could be explained by a higher alpha contribution than expected due to pure beam-target fusion. Future investigations with improved diagnostics and better-controlled catcher plates might reveal higher alpha yields than those calculated here.
Both the activation measurements and corresponding calculations show that it should be possible to design a catcher material composition that triggers selected multiple nuclear reactions that can be used to infer the primary particle energy distributions with sufficient accuracy. In a similar vein, we show that, while neutron spectroscopy in BN targets may not be used as a diagnostic tool for alpha particles when fast protons are present, the close resemblance of the measured and calculated data for protons demonstrates its high potential as a diagnostic for the proton distribution. Such nuclear diagnostics will become relevant for diagnosing the particle distributions inside integrated fusion devices, such as, for example, the emerging, laser-driven, and mixed-fuel microreactor concept [Reference Ruhl and Korn1].
Data Availability
The data used to support the findings of this study can be obtained from the corresponding author upon reasonable request.
Conflicts of Interest
MS, VS, CC, SvS, and GK are or were employed at Marvel Fusion GmbH.
Acknowledgments
The authors would like to thank Juliana Metzler and Marco Tosca for their help with CR39 analysis and Hartmut Ruhl for fruitful discussions about laser-driven particle acceleration and proton-boron fusion. J. J. Rocca acknowledges the support of a DOD Vannevar Bush Faculty Fellowship, ONR award N000142012842. The experiments were performed at the ALEPH laser facility at Colorado State University supported by LaserNetUS under grant US DE-SC0019076 from the U.S. Department of Energy. This work was funded by Marvel Fusion GmbH.











