Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T12:12:26.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinetic extraordinary-mode eigenvalue equation for relativistic nonneutral electron flow in planar geometry

Published online by Cambridge University Press:  09 March 2009

Ronald C. Davidson  and
Han S. Uhm
Ronald C. Davidson
Affiliation:
Plasma Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139
Han S. Uhm
Affiliation:
Naval Surface Warfare Center, Silver Spring, MD 20903
Get access Rights & Permissions [Opens in a new window]

Abstract

Use is made of the Vlasov–Maxwell equations to derive an eigenvalue equation describing the extraordinary–mode stability properties of relativistic, non-neutral electron flow in high-voltage diodes. The analysis is based on well-established theoretical techniques developed in basic studies of the kinetic equilibrium and stability properties of nonneutral plasmas characterized by intense self fields. The formal eigenvalue equation is derived for extraordinary-mode flute perturbations in a planar diode. As a specific example, perturbations are considered about the choice of self-consistent Vlasov equilibrium 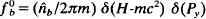, where 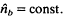. is the electron density at the cathode (x = 0), H is the energy, and Py is the canonical momentum in the Y-direction (the direction of the equilibrium electron flow). As a limiting case, the planar eigenvalue equation is further simplified for low-frequency long-wavelength perturbations with |ω − kvd, ≪ ωυ where 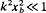and 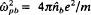and ⋯c = eB0/mc, and B0ệz is the applied magnetic field in the vacuum region xb < x ≤ d. Here, the outer edge of the electron layer is located at x = xb; ω is complex oscillation frequency; k is the wavenumber in the y-direction; ωυ is the characteristic betatron frequency for oscillations in the x′-orbit about the equilibrium value x′ = x0 = xb/2; and Vd is the average electron flow velocity in the y-direction at x = x0. In simplifying the orbit integrals, a model is adopted in which the eigenfunction approximated by 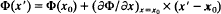, where x′(t′) is the x′-orbit in the equilibrium field configuration. A detailed analysis of the resulting eigenvalue equation for 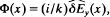, derived for low-frequency long-wavelength perturbations, is the subject of a companion paper.

Type
Research Article
Information
Laser and Particle Beams , Volume 7 , Issue 1 , February 1989 , pp. 55 - 84
Copyright
Copyright © Cambridge University Press 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bekefi, G. 1982 Appl. Phys. Lett. 40, 2319.CrossRefGoogle Scholar
Briggs, R. J., Daugherty, J. D. & Levy, R. H. 1970 Phys. Fluids 13, 421.Google Scholar
Buneman, O., Levy, R. H. & Linson, L. M. 1966 J. Appl. Phys. 37, 3203.Google Scholar
Chang, C. L., Antonsen, T. M. Jr. & Drobot, A. T. 1984 Phys. Fluids 27, 2545.CrossRefGoogle Scholar
Chang, C. L. et al. 1984 Phys. Fluids 27, 2937.CrossRefGoogle Scholar
Chernin, D. & Lau, Y. Y. 1984 Phys. Fluids 27, 2319.CrossRefGoogle Scholar
Davidson, R. C. 1974 Theory of Nonneutral Plasmas (Benjamin, Reading, Mass.).Google Scholar
Davidson, R. C. & Uhm, H. S. 1982 Phys. Fluids 25, 2089.Google Scholar
Davidson, R. C. & Tsang, K. T. 1984 Phys. Rev. 29, 488.CrossRefGoogle Scholar
Davidson, R. C., Tsang, K. T. & Swegle, J. A. 1984 Phys. Fluids 27, 2332.Google Scholar
Davidson, R. C. 1984 Handbook of Plasma Physics—Volume 2: Basic Plasma Physics II (eds. Galeev, A. A. & Sudan, R. N., Elsevier, New York) pp. 768—816.Google Scholar
Davidson, R. C., McMullin, W. A. & Tsang, K. T. 1984 Phys. Fluids 27, 233.CrossRefGoogle Scholar
Davidson, R. C. & Tsang, K. T. 1985 Phys. Fluids 28, 1169.Google Scholar
Davidson, R. C., Tsang, K. T. & Uhm, H. S. 1985 Phys. Rev. A32, 1044.CrossRefGoogle Scholar
Davidson, R. C. & Uhm, H. S. 1985 Phys. Rev. A32, 3554.CrossRefGoogle Scholar
Davidson, R. C. 1985a Phys. Fluids 28, 377.Google Scholar
Davidson, R. C. 1985b J. Plasma Phys. 33, 157.Google Scholar
Davidson, R. C. 1985C Phys. Fluids 28, 1937.Google Scholar
Davidson, R. C. & Uhm, H. S. 1989 “Kinetic Stability Properties of Relativistic Nonneutral Electron Flow for Low-Frequency Extraordinary-Mode Perturbations” Laser and Particle Beams, in press.CrossRefGoogle Scholar
Lau, Y. Y. 1984 Phys. Rev. Lett. 53, 395.CrossRefGoogle Scholar
Levy, R. H. 1965 Phys. Fluids 8, 1288.CrossRefGoogle Scholar
Mendel, C. W. Jr., Seidel, D. B. & Slutz, S. A. 1983 Phys. Fluids 26, 3628.CrossRefGoogle Scholar
Mendel, C. W. Jr., Swegle, J. A. & Seidel, D. B. 1985 Phys. Rev. A32, 1091.CrossRefGoogle Scholar
Miller, R. B. 1982 Intense Charged Particle Beams (Plenum, New York).Google Scholar
Orzechowski, T. J. & Bekefi, G. 1979 Phys. Fluids 22, 978.CrossRefGoogle Scholar
Palevsky, A. & Bekefi, G. 1979 Phys. Fluids 22, 986.CrossRefGoogle Scholar
Rostoker, N. 1973 Particle Accelerators 5, 93.Google Scholar
Rostoker, N. 1980 Comments Plasma Phys. Controlled Fusion Res. 6, 91.Google Scholar
Sprangle, P. & Kapetanakos, C. A. 1978 J. Appl. Phys. 49, 1.CrossRefGoogle Scholar
Swegle, J. & Ott, E. 1981a Phys. Rev. Lett. 46, 929.CrossRefGoogle Scholar
Swegle, J. & Ott, E. 1981b Phys. Fluids 24, 1821.CrossRefGoogle Scholar
Swegle, J. 1983 Phys. Fluids 26, 1670.Google Scholar
Uhm, H. S. & Davidson, R. C. 1985 Phys. Rev. A31, 2556.CrossRefGoogle Scholar
Uhm, H. S., Davidson, R. C. & Petillo, J. 1985 Phys. Fluids 28, 2537.CrossRefGoogle Scholar
Vandevender, J. P. et al. 1981 J. Appl. Phys. 52, 4.CrossRefGoogle Scholar
Vandevender, J. P. et al. 1985 Proc. International Conference on Plasma Physics and Controlled Nuclear Fusion Research(IAEA,Vienna,1984),Nucl. Fusion Suppl. 3, 59 and references therein.Google Scholar
Voronen, V. S. & Lebedev, A. N. 1973 Zh. Tekh. Fiz. 43, 2591 [1974 Sov. Phys.-Tech. Phys. 18, 1627.].Google Scholar