1. Introduction
Bow wave is a common phenomenon that can be observed in fluid and gas. When a ship sails in the sea, in addition to the backward Kelvin wave, a specific wave will also be generated at the bow position, which determines the outer boundary of the wave it makes [Reference Lamb1], and this is the bow wave. The bow wave not only consumes ship’s energy but also damages coastal facilities and over-water buildings. Therefore, reducing the impact of the bow wave is an important goal of shipbuilding industry. In the air, when the aircraft breaks through the sound barrier, it will trigger a specific bow wave and the associated Prandtl–Glauert condensation cloud [Reference Erich2].
Bow waves are also found in space, such as the bow shock wave produced when the solar wind meets the Earth’s magnetic field. At present, the largest observed head wave is observed by the Spitzer Space Telescope in galaxy collision [Reference Appleton, Xu and Reach3]. As can be seen from the above examples, bow waves can lead to a large number of physical processes, such as the transverse transfer of momentum and matter and particle acceleration.
It is well known that the ultra-short laser pulse propagating in the low-density plasma can excite the wake waves [Reference Tajima and Dawson4, Reference Zhang, Ma and Zou5], which is very similar to the Kelvin wave generated by the ship sailing in the sea. In addition to the wake waves, the laser pulse can also excite the bow waves in the collisionless plasma. Like a ship’s bow wave, the bow wave generated by a laser pulse also disperses the energy and momentum of the laser pulse to the sides. The concept of bow waves in laser plasma was first proposed by Esirkepov et al. [Reference Esirkepov, Kato and Bulanov6] in 2008. It was revealed that transverse modulation of electron density caused by the bow wave can effectively increase the potential of wakefield. In recent years, a large number of researchers have paid attention to laser wakefield acceleration (LWA) [Reference Esarey, Schroeder and Leemans7–Reference Wang, Wang and Dong11], but few of them have detailed analysis about bow waves. Further study of bow waves will help to further understand the crucial problems of wakefield acceleration, such as the motion of electrons in the wakefield and bow wave, as well as the high-order harmonics generated by them.
Research about the electron motion related to the wakefield is important not only to the LWA but also to the radiation produced by the ultra-fast electron beam and the electron “flying mirror” regime. Coherent ultra-short radiation source is an important tool to explore and control the microcosmic world [Reference Krausz and Ivanov12, Reference Corde, Ta Phuoc and Lambert13]. The electron beam accelerated by the wakefield can generate ultra-short pulses and high-order harmonics [Reference Sheng, Mima, Zhang and Sanuki14, Reference Pirozhkov, Kando and Esirkepov15]. Moreover, high-frequency pulses [Reference Esirkepov, Mu and Gu16] and self-generated magnetic field can be generated by using ultra-fast electrons to reflect the probe light [Reference Mu, Li, Sheng and Zhang17].
When a focused laser pulse propagates in under-dense plasma, if the spot size of the laser is smaller than the wavelength of the wakefield, the electrons expelled by the laser cannot be trapped by the wakefield. The electrons will move to the sides, forming the bow wave of the wakefield. So far, there are few studies on the bow waves in laser plasma. In this paper, the effects of laser and plasma parameters on the bow wave properties are studied in detail. The density of the electron layer at the junction of the wakefield and the bow wave is much higher than that at the bottom of the wakefield, and the longitudinal velocity is close to the speed of light. By using the ultra-dense energetic electron layer at the joining part of the bow wave and wake wave as a “flying mirror” to reflect laser pulse, we can obtain high-order harmonics with upshifted frequency [Reference Mu, Esirkepov and Valenta18]. In this paper, we investigated how the open angle, transverse momentum of the bow wave, and the peak density are influenced by the initial density of plasma, laser intensity, focal spot size, and preplasma length. It helps to further understand the formation of the wakefield and bow wave, the mechanism of high-order harmonic generation, and coherent Thomson scattering.
2. Simulation Parameters
Two-dimensional and three-dimensional numerical simulations of the interaction between laser and under-dense plasma were carried out by particle-in-cell (PIC) code EPOCH [Reference Arber, Bennett and Brady19]. In 2D simulations: the size of simulation box is
![]() and the mesh number is 1600 × 800, where
and the mesh number is 1600 × 800, where
![]() is the wavelength of incident laser in vacuum. The number of macroparticles is 5120000. The fully ionized plasma is located at
is the wavelength of incident laser in vacuum. The number of macroparticles is 5120000. The fully ionized plasma is located at
![]() and the density is
and the density is
![]() . The initial intensity of the laser pulse is
. The initial intensity of the laser pulse is
![]() , corresponding to the dimensionless amplitude
, corresponding to the dimensionless amplitude
![]() which propagates forward along the x-axis and is linearly polarized along the y-axis, the full width at half maximum of the transverse focal spot is 10μm, and the FWHM of the pulse width is
which propagates forward along the x-axis and is linearly polarized along the y-axis, the full width at half maximum of the transverse focal spot is 10μm, and the FWHM of the pulse width is
![]() .
.
![]() is the laser frequency, e and me denote the charge and mass of the electron, E 0 is the amplitude of the laser electric field, c is the speed of light in vacuum, and T 0 is the laser period. The ions are assumed as stationary, that is, the mass ratio of ion to electron is
is the laser frequency, e and me denote the charge and mass of the electron, E 0 is the amplitude of the laser electric field, c is the speed of light in vacuum, and T 0 is the laser period. The ions are assumed as stationary, that is, the mass ratio of ion to electron is
![]()
The wakefield and bow wave can be observed in a wide range of parameters. Parameters in the three-dimensional simulation are as follows: the size of the simulation box is
![]() and the mesh number is 660 × 900 × 900. The number of macroparticles is
and the mesh number is 660 × 900 × 900. The number of macroparticles is
![]() . The fully ionized plasma is distributed in the whole simulation space with the density of
. The fully ionized plasma is distributed in the whole simulation space with the density of
![]() The initial intensity of the laser pulse is
The initial intensity of the laser pulse is
![]() , corresponding to the dimensionless amplitude
, corresponding to the dimensionless amplitude
![]() which propagates forward along the x-axis and is linearly polarized along the y-axis, the FWHM transverse focal spot is 6.7μm, and the FWHM pulse duration is
which propagates forward along the x-axis and is linearly polarized along the y-axis, the FWHM transverse focal spot is 6.7μm, and the FWHM pulse duration is
![]() .
.
3. Simulation Results and Analysis
When the laser pulse enters the plasma region, a strong wakefield will be excited. Under the ponderomotive force and electromagnetic force of the laser field, electrons will be expelled to all directions to form a bubble structure without electrons inside, as shown in the electron density distribution in Figure 1. The electric field not only pushes the electrons in the longitudinal direction but also pushes the electrons in the transverse direction, forming bow waves on both sides of the wakefield.
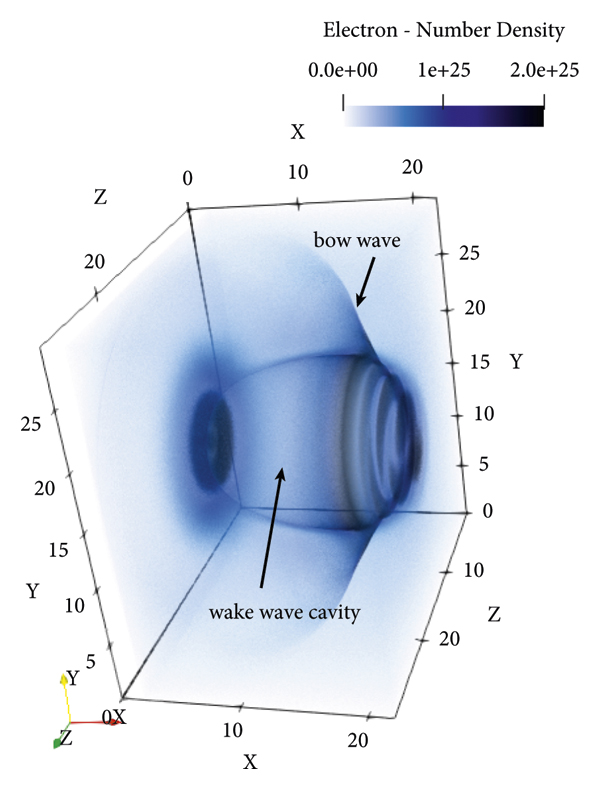
Figure 1: The electron density distribution at 24T 0.
For the wakefield and bow wave, two-dimensional simulation is launched for further analysis. The electron density distribution is shown in Figures 2(a)–2(d). Figures 2(b) and 2(c) show the distribution of electron density along the dotted line x = 63μm and y = 14μm in Figure 2(a), respectively. The electron number density at the bow wave reaches
![]() . The electron density of the bow wave increases gradually along the +x direction and reaches the maximum at the joining part of the bow wave and the wakefield. At this time
. The electron density of the bow wave increases gradually along the +x direction and reaches the maximum at the joining part of the bow wave and the wakefield. At this time
![]() the peak electron number density is about
the peak electron number density is about
![]() , which is much higher than the density at the bottom of the wakefield, reaching more than 30 times the initial electron density. The ultra-dense electron layer at the joining part of the bow wave and wake wave has a velocity close to the speed of light. It can be used as a creative “flying mirror” to reflect laser pulses. According to the coherent Doppler effect, the frequency of the reflected laser pulse will be upshifted by 4γ 2, where
, which is much higher than the density at the bottom of the wakefield, reaching more than 30 times the initial electron density. The ultra-dense electron layer at the joining part of the bow wave and wake wave has a velocity close to the speed of light. It can be used as a creative “flying mirror” to reflect laser pulses. According to the coherent Doppler effect, the frequency of the reflected laser pulse will be upshifted by 4γ 2, where
![]() , v is the velocity of the electron layer, and c is the speed of light in vacuum [Reference Bulanov, Esirkepov, Kando, Pirozhkov and Rosanov20–Reference Mu, Li, Zeng, Chen, Sheng and Zhang22]. As shown in Figures 2(e) and 2(f), the distribution area of longitudinal electric field Ex is much larger than that of wakefield cavity. Thus, the potential is not limited by the wake cavity size.
, v is the velocity of the electron layer, and c is the speed of light in vacuum [Reference Bulanov, Esirkepov, Kando, Pirozhkov and Rosanov20–Reference Mu, Li, Zeng, Chen, Sheng and Zhang22]. As shown in Figures 2(e) and 2(f), the distribution area of longitudinal electric field Ex is much larger than that of wakefield cavity. Thus, the potential is not limited by the wake cavity size.
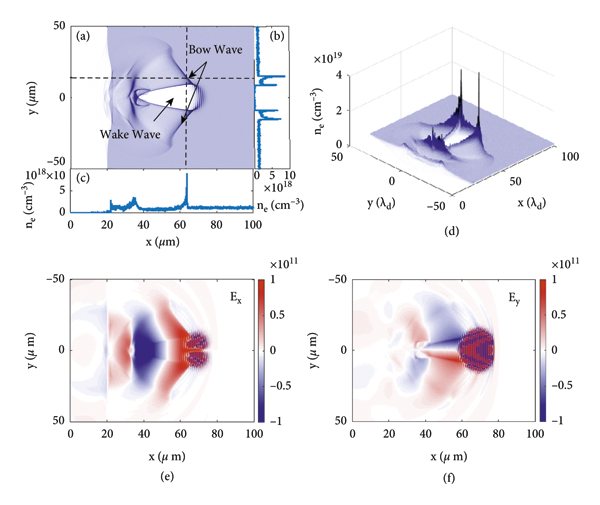
Figure 2: 2D simulation results at 78T 0. (a)–(d) Electron density distribution in the (x, y) plane, (b) and (c) are the distributions along the dashed lines x = 63 μm and y = 14 μm in (a), (d) is the distribution with the number density shown in z-axis, and (e) and (f) are the longitudinal transverse electric fields, respectively, in the (x, y) plane.
The longitudinal and transverse electron momentum is shown in Figure 3. Due to transverse wave breaking, the electrons move outwards transversely, increasing the potential in the wakefield. Therefore, wake breaking is mainly aroused by the self-generated electrostatic field in the wakefield caused by the tightly focused laser [Reference Bulanov, Pegoraro, Pukhov and Sakharov23]. The bow wave is piled up by the electrons directly accelerated by the laser ponderomotive force. When the laser enters the plasma, the electrons move forward and at the same time transversely to both sides continuously, gradually increasing the area of bow wave. Unlike the wake wave cavity easily being destroyed by electron injection, the properties of the bow wave are usually stable, as the laser propagates.
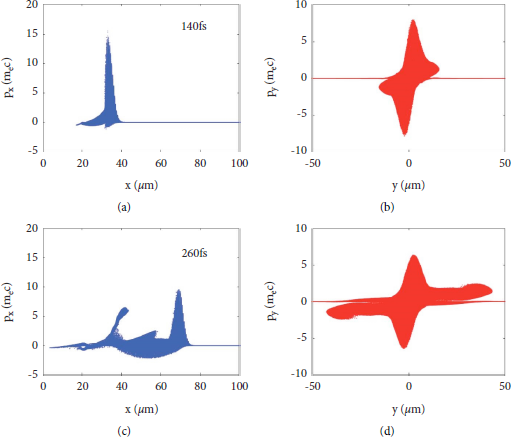
Figure 3: Longitudinal (a, c) and transverse (b, d) electron momentum at 42T 0 and 78T 0.
The structures of the wake waves and bow waves produced by different laser and plasma parameters are shown in Figure 4. The laser with higher intensity generates stronger ponderomotive force
![]() . Therefore, with more intense laser, larger number of electrons will be expelled to the transverse sides, under larger ponderomotive force. As a result, the angle θ between the bow wave and the wake wave boundary is larger. The longitudinal length of the wake wave cavity is larger due to stronger electrostatic field and ponderomotive force, as shown in Figures 4(a) and 4(b). Denser plasma will repress the effect of ponderomotive force, resulting in shorter wake wave cavity and larger angle θ, as shown in Figures 4(c) and 4(d).
. Therefore, with more intense laser, larger number of electrons will be expelled to the transverse sides, under larger ponderomotive force. As a result, the angle θ between the bow wave and the wake wave boundary is larger. The longitudinal length of the wake wave cavity is larger due to stronger electrostatic field and ponderomotive force, as shown in Figures 4(a) and 4(b). Denser plasma will repress the effect of ponderomotive force, resulting in shorter wake wave cavity and larger angle θ, as shown in Figures 4(c) and 4(d).

Figure 4: Electron density distribution with respect to laser intensity of (a)
![]() and (b)
and (b)
![]() , plasma density of (c)
, plasma density of (c)
![]() and (d)
and (d)
![]() , and laser focal spot size of (e) 8μm and (f) 20μm (g) without preplasma and (h) with preplasma at 78T 0.
, and laser focal spot size of (e) 8μm and (f) 20μm (g) without preplasma and (h) with preplasma at 78T 0.
The laser focal spot size is 8μm and 20μm, and the latter is closer to the matched spot size of a self-focused laser
![]() . Here
. Here
![]() , where ε is the vacuum dielectric constant. The laser intensity hardly decays during the simulation with spot size of 20μm [Reference Lu, Tzoufras and Joshi24]. The electrostatic field is stronger and ponderomotive force is smaller, as shown in Figures 4(e) and 4(f). The preplasma can restrain the wave breaking and increase the energy of transverse ponderomotive force, so the distribution range of the bow wave in transverse direction is larger.
, where ε is the vacuum dielectric constant. The laser intensity hardly decays during the simulation with spot size of 20μm [Reference Lu, Tzoufras and Joshi24]. The electrostatic field is stronger and ponderomotive force is smaller, as shown in Figures 4(e) and 4(f). The preplasma can restrain the wave breaking and increase the energy of transverse ponderomotive force, so the distribution range of the bow wave in transverse direction is larger.
Laser and plasma parameters play important roles in the structure and distribution of wake wave and bow wave, as well as the electron momentum. The transverse momentum distribution of electrons is shown in Figure 5. Increasing laser intensity will directly enhance the laser ponderomotive force and thus increase the transverse momentum of electron in wakefield and bow wave. Increasing electron density will lead to immature electron injection. The longitudinal momentum of the injected electron increases sharply, while the transverse and longitudinal momentum of the electron at the bow wave decreases. The focal spot size of the laser increases from 8μm to 20μm, closer to the matched laser self-focusing radius. The laser with larger spot size makes the normalized electric field amplitude increase from
![]() to
to
![]() , enhancing the wakefield and bow wave, as well as the electron momentum.
, enhancing the wakefield and bow wave, as well as the electron momentum.
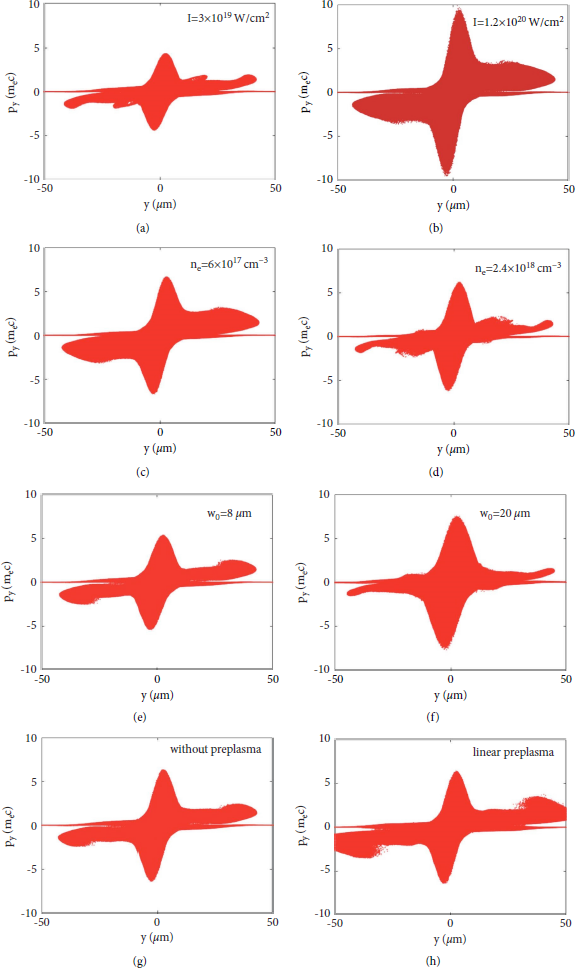
Figure 5: Electron momentum distribution with respect to laser intensity of (a)
![]() and (b)
and (b)
![]() , plasma density of (c)
, plasma density of (c)
![]() and (d)
and (d)
![]() , and laser focal spot size of (e)8μm and (f)20μm (g) without consideration of preplasma and (h) linear increasing preplasma at 78T 0.
, and laser focal spot size of (e)8μm and (f)20μm (g) without consideration of preplasma and (h) linear increasing preplasma at 78T 0.
By changing the laser intensity, plasma density, laser focal spot size, and length of preplasma, the effects of laser and plasma parameters on the structure, density, and electron momentum of the bow wave are further studied. The bow wave can be produced within a wide range of parameters, but sometimes it is difficult to distinguish because it is located near the wake wave. It is found that the angle θ of the bow wave to the boundary of wake wave cavity is closely related to laser parameters such as laser intensity and focal spot radius. With higher laser intensity, θ increases obviously and the bow wave structure is easier to observe, as shown in Figures 4(a), 4(b), and 6(a). When the laser focal spot radius increases from 8μm to 20μm, it is closer to the matched radius of the wakefield acceleration, and the wakefield energy and electron momentum are enhanced, but the angle θ between the bow wave and the wakefield wall decreases, as shown in Figures 4(e), 4(f), and 6(c). When the laser focal spot is reduced to 5μm, with the propagation of the laser, the laser will be defocused. With a 0 becoming smaller, θ decreases sharply and the shape of the bow wave becomes irregular. With increasing plasma density from
![]() to
to
![]() , the angle θ decreases gradually, as shown in Figures 5(c), 5(d), and 6(b). When the preplasma is introduced, the angle θ is increased, as shown in Figures 5(g), 5(h), and 6(d).
, the angle θ decreases gradually, as shown in Figures 5(c), 5(d), and 6(b). When the preplasma is introduced, the angle θ is increased, as shown in Figures 5(g), 5(h), and 6(d).
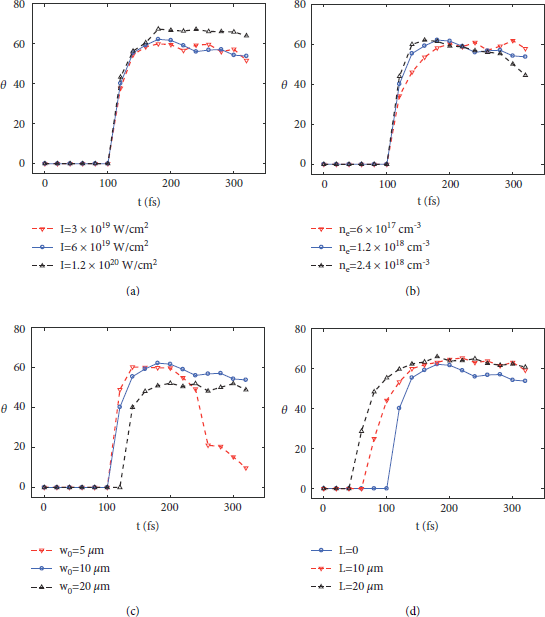
Figure 6: The evolution of the angle between the wake wave cavity wall and the bow wave with respect to the laser and plasma parameters. (a)–(d) correspond to the influence of laser intensity, plasma density, laser spot size, and the length of preplasma.
As the laser interacts with the plasma, the electrons pile up to form the wake wave, and the electron transverse momentum increases. After the whole laser pulse entered the plasma and the wake wave cavity is completely formed, the transverse momentum of the electron decreases slowly, as shown in Figure 7. With the increase of laser intensity and focal spot radius, the transverse momentum of electrons increases significantly, enlarging the bow wave area. When the plasma density increases from
![]() to
to
![]() , the transverse momentum and longitudinal momentum of electron decrease correspondingly until electron injection occurs. When the laser focal spot increases, the transverse momentum of electron decreases more slowly. With a FWHM focal spot size of w 0 = 20μm, approximately equal to self-focusing matched size, the electron transverse momentum does not decay with time. The preplasma makes the laser interact with plasma earlier, and after the whole laser pulse entered the plasma, the electron transverse momentum is no longer influenced.
, the transverse momentum and longitudinal momentum of electron decrease correspondingly until electron injection occurs. When the laser focal spot increases, the transverse momentum of electron decreases more slowly. With a FWHM focal spot size of w 0 = 20μm, approximately equal to self-focusing matched size, the electron transverse momentum does not decay with time. The preplasma makes the laser interact with plasma earlier, and after the whole laser pulse entered the plasma, the electron transverse momentum is no longer influenced.
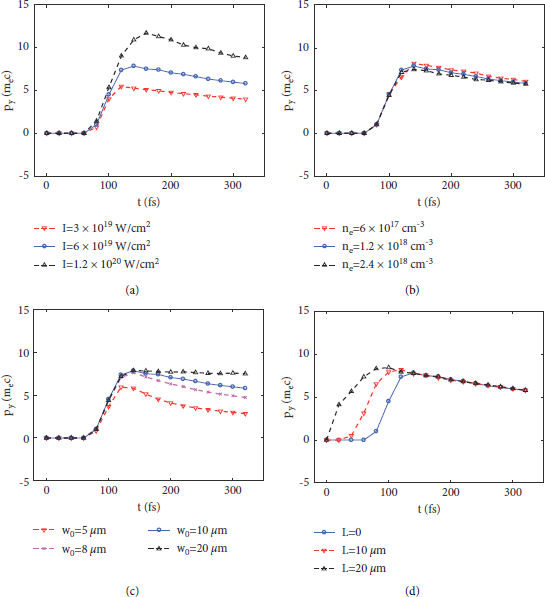
Figure 7: The evolution of the electron transverse momentum with respect to the laser and plasma parameters.
The electron density of the bow wave increases near the front and central area. A density peak is generated at the joining part of the bow wave and the wake cavity wall. The peak density fluctuates with time, but the overall trend is positively correlated with laser intensity and plasma density, as shown in Figures 8(a) and 8(b). This effect gets saturated when the laser intensity is over
![]() and when the density exceeds
and when the density exceeds
![]() . The peak density of the bow wave has no correlation with the size of the laser focal spot and the length of the preplasma, but when the laser focal spot is too small for the self-focusing effect, laser defocusing causes the density peak to decrease, as shown in Figures 8(c) and 8(d).
. The peak density of the bow wave has no correlation with the size of the laser focal spot and the length of the preplasma, but when the laser focal spot is too small for the self-focusing effect, laser defocusing causes the density peak to decrease, as shown in Figures 8(c) and 8(d).
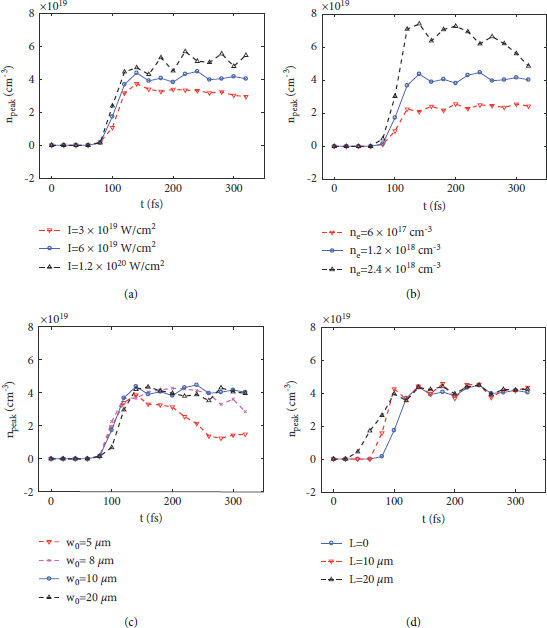
Figure 8: The evolution of the electron peak density of the bow wave with respect to the laser and plasma parameters.
4. Conclusion
In this paper, multidimensional PIC code is used to simulate the generation of the wakefield and bow wave by the interaction of laser and plasma. By analyzing the influence of laser and plasma parameters on the structure of the bow wave, the peak electron density, and the electron momentum, the properties of the bow wave in the wakefield are further explored. The results show that increasing the laser intensity and reducing the plasma density are beneficial to the observation of the bow wave in the laser-induced wakefield, and the introduction of the preplasma is also helpful to observe the bow wave. When the focal spot size of the Gaussian laser beam is smaller than the matched self-focused laser in the wakefield, the transverse momentum of the electron is positively correlated with the focal spot radius. At the joining part of the bow wave and the wake cavity wall, the electron density is very high. The peak density is positively correlated with the laser intensity and plasma density. This high-density electron peak can be used as a new kind of electronic “flying mirror” to generate high-frequency high-order harmonics. This paper is innovative and forward-looking in the study of the bow wave of the wakefield, which is helpful to further understand the motion of electrons in the laser wakefield and bow wave, and has significance for the generation of high-frequency ultra-short pulses through a new kind of electronic “flying mirror.” The work on laser and plasma is also beneficial to satellite laser communication.
Data Availability
The data used to support the findings of this study are included within the supplementary information file.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
This study was supported by the National Science Foundation of China (grant no. 12205191) and Shanghai Science and Technology Commission (grant no. 21DZ1206500). The EPOCH code was in part funded by the UK EPSRC (grant nos. EP/G054950/1, EP/G056803/1, EP/G055165/1, and EP/M022463/1).
Supplementary Materials
The supplementary file includes the 2D density data of the simulation results. One can easily draw a 2D distribution of the density and see the bow waves. (Supplementary Materials)

















