Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T05:03:25.037Z Has data issue: false hasContentIssue false
  • English
  • Français

Parametric excitation of surface plasma waves over a metallic surface by laser in an external magnetic field

Published online by Cambridge University Press:  05 February 2018

Prashant Chauhan ,
Deepika Goel ,
Anshu Varshney ,
D. B. Singh  and
Vivek Sajal
Prashant Chauhan*
Affiliation:
Department of Physics and Material Science & Engineering, Jaypee Institute of Information Technology, Noida-201307, Uttar Pradesh, India
Deepika Goel
Affiliation:
Department of Physics and Material Science & Engineering, Jaypee Institute of Information Technology, Noida-201307, Uttar Pradesh, India
Anshu Varshney
Affiliation:
Department of Physics and Material Science & Engineering, Jaypee Institute of Information Technology, Noida-201307, Uttar Pradesh, India
D. B. Singh
Affiliation:
Department of Physics and Material Science & Engineering, Jaypee Institute of Information Technology, Noida-201307, Uttar Pradesh, India
Vivek Sajal
Affiliation:
Department of Physics and Material Science & Engineering, Jaypee Institute of Information Technology, Noida-201307, Uttar Pradesh, India
*
Author for correspondence: Prashant Chauhan, Department of Physics and Material Science & Engineering, Jaypee Institute of Information Technology, Noida-201307, Uttar Pradesh, India, E-mail: prashant.k.chauhan@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Effects of external static magnetic field (applied in 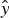$\hat y$-direction) on resonant excitation of surface plasma waves (SPW) have been investigated over the metal free space interface. The high power laser $({\rm \omega} _0,\;\vec k_{0z})$ is incident over the metal surface and exerts a ponderomotive force on the metal electrons in the skin layer. The ponderomotive force disturbs the quasi-neutrality of plasma which results into the excitation of space charge field at the frequency 2ω0. The electron density perturbation at frequency 2ω0 driven by self-consistent space charge potential couples with the oscillatory velocity due to the seed SPW 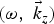$({\rm \omega}, \;\vec k_z)$ and produces nonlinear current to drive another counter propagating SPW 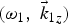$({\rm \omega} _1,\;\vec k_{1z})$ at the phase matching conditions of frequency ω = ω1 − 2ω0 and wavenumber 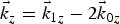$\vec k_z = \vec k_{1z} - 2\vec k{}_{0z}$ (by feedback mechanism). The parametric process becomes resonant at 2ω0 ≈ ωp and the maximum growth rate is achieved for an incidence angle of laser θ = 40°. The growth rate of the process reduces to half on increasing the magnetic field from 0.49 to 2.45 MG. The present study may be significant to the laser absorption experiments where surface rippling can strongly affect the laser energy absorption.

Keywords

Lasermagnetic fieldparametric excitationsurface plasma waves
Type
Research Article
Information
Laser and Particle Beams , Volume 36 , Issue 1 , March 2018 , pp. 92 - 97
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baeva, T, Gordienko, S and Pukhov, A (2006) Theory of high harmonic generation in relativistic laser interaction with overdense plasma. Physical Review E 74, 046404.Google Scholar
Brodin, G and Lundberg, J (1991) Parametric excitation of surface waves in a strongly inhomogeneous plasma. Journal of Plasma Physics, 46, 299–307.CrossRefGoogle Scholar
Bulanov, SV, Naumova, NM and Pegoraro, F (1994) Interaction of ultrashort, relativistically strong laser pulse with overdense plasma. Physics of Plasmas 1, 745.Google Scholar
Goel, D, Chauhan, P, Varshney, A, Singh, DB and Sajal, V (2015) Stimulated Compton scattering of surface plasma wave excited over metallic surface by a laser. Laser and Particle Beams 33, 641–646.Google Scholar
Hosokai, T, Kinoshita, K, Zhidkov, A, Maekawa, A, Yamazaki, A and Uesaka, M (2006) Effect of external static magnetic field on the emittance and total charge of electron beams generated by Laser-Wakefield acceleration. Physics Review Letters 97, 075004.Google Scholar
Kretschmann, E and Reather, H (1968) Radiative decay of non radiative surface plasmons excited by light. Z. Naturforschung 23a, 2135–2136.Google Scholar
Kumar, N and Tripathi, VK (2007) Parametric excitation of surface plasma waves in an overdense plasma irradiated by an ultrashort laser pulse. Physics of Plasma 14, 103108.Google Scholar
Lagutin, A, Rosseel, K, Herlach, F, Vanacken, J and Bruynseraede, Y (2003) Development of reliable 70T pulsed magnets. Measurement Science Technology 14, 2144–2150.Google Scholar
Lee, HJ and Cho, SH (1999) Parametric coupling of light wave and surface plasma waves. Physical Review E 59 3, 3503–3511.CrossRefGoogle Scholar
Macchi, A, Battaglini, M, Cornolti, F, Lisseikina, TV, Pegoraro, F, Ruhl, H and Vshivkov, VA (2002) Parametric generation of surface deformations in laser interaction with overdense plasmas. Laser and Particle Beams 20, 337–340.Google Scholar
Macchi, A, Cornolti, F, Pegoraro, F, Lisseikina, TV, Ruhl, H and Vshivkov, VA (2001) Surface oscillations in overdense plasmas irradiated by ultrashort laser pulses. Physical Review Letters 87, 205004.CrossRefGoogle ScholarPubMed
Nalini, N, Kaushic, TC and Gupta, SC (2010) Generation and measurement of multi megagauss field in inertial magnets. Sadhana, Bol 35(5), 547–566.CrossRefGoogle Scholar
Parashar, J, Pandey, HD and Tripathi, VK (1998) Laser excitation of surface waves over a dense plasma. Journal of Plasma Physics 59, 97–102.Google Scholar
Raether, H (1988) Surface Plasmons on Smooth and Rouge Surfaces and on Gratings. Springer-Verlag Berlin Heidelberg.Google Scholar
Singh, DB and Tripathi, VK (2007) Laser beat wave excitation of surface plasma wave and material ablation. Physics of Plasma 14, 103115.Google Scholar
Yasumoto, K (1981) Electromagnetic decay into two surface plasma wave and an ion acoustic surface wave in a semi-infinite plasma. Journal of Applied Physics 52, 3238.Google Scholar
Yasumoto, K and Noguchi Verma, T (1982) Electromagnetic decay into two surface plasma waves in a semi –infinite plasma. Journal of Applied Physics 53, 208–214, 10.1063/1.331594.Google Scholar