Introduction
Ultra-short X ray is a powerful tool for detecting the atom and molecule motions within the femtosecond time scale (Attwood, Reference Attwood1999). Among many methods of generating X-ray pulses, Thomson scattering source is a promising way to produce quasi-monoenergetic and energy tunable X-ray pulses with femtosecond duration and high brightness (Sprangle and Esarey, Reference Sprangle and Esarey1992; Sprangle et al., Reference Sprangle, Ting, Esarey and Fisher1992). But the tiny cross section of the Thomson scattering and the low photon yield restrict the practical applications. To increase the photon yield, the high-density electron layer produced by laser–plasma interaction is suggested as a relativistic electron mirror (REM) to reflect another laser beam (Bulanov et al., Reference Bulanov, Esirkepov and Tajima2003), where the high electron density will lead to much higher photon yield. This method opens a possible way to generate ultra-high intense electromagnetic fields toward the Schwinger limit.
The numerical studies on the interaction between ultra-high contrast laser and solid nanofilm targets show the possibility to directly push a whole electron layer from the targets (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2007). The REM radiation studies have attracted many theoretical (Habs et al., Reference Habs, Hegelich, Schreiber, Gross, Henig, Kiefer and Jung2008; Esirkepov et al., Reference Esirkepov, Bulanov, Zhidkov, Pirozhkov and Kando2009; Meyer-ter-Vehn and Wu, Reference Meyer-ter-Vehn and Wu2009; Wen et al., Reference Wen, Wu, Meyer-ter-Vehn and Shen2009, Reference Wen, Jin, Lu, Chen and Yan2012; Wu and Meyer-ter-Vehn, Reference Wu and Meyer-ter-Vehn2009; Wu et al., Reference Wu, Meyer-ter-Vehn, Fernández and Hegelich2010, Reference Wu, Meyer-ter-Vehn, Hegelich and Fernández2011; Wu, Reference Wu2011; Tan et al., Reference Tan, Wu, Zhu, Han, Zhao, Hong, Cao and Gu2012) and experimental efforts (Kiefer et al., Reference Kiefer, Henig, Jung, Gautier, Flippo, Gaillard, Letzring, Johnson, Shah, Shimada, Fernández, Liechtenstein, Schreiber, Hegelich and Habs2009, Reference Kiefer, Yeung, Dzelzainis, Foster, Rykovanov, Lewis, Marjoribanks, Ruhl, Habs, Schreiber, Zepf and Dromey2013). In recently review papers (Bulanov et al., Reference Bulanov, Esirkepov, Kando, Pirozhkov and Rosanov2013, Reference Bulanov, Esirkepov, Kando and Koga2016), the mechanism of generating the REM and frequency upshifted radiation pulse have been presented. Although the reflectivity of relativistic ultra-thin electron layers can be analytically derived (Wu and Meyer-ter-Vehn, Reference Wu and Meyer-ter-Vehn2009; Bulanov et al., Reference Bulanov, Esirkepov, Kando and Koga2016), the reflectivity under the resonance condition, when the plasma frequency of the REM equal to the laser frequency, cannot be well described.
In this paper, the simulation results for the generation of REM and the reflection of an ultra-short probe laser off the REM are introduced. Rapidly accelerating and expanding REM can be generated from a nanofoil target illuminated normally by an ultra-intense femtosecond laser pulse. Isolated chirped radiation pulse can be produced from the reflection of a counter-propagating probe laser on the REM. In the reflected radiation field, an unusual intense peak is observed. Considering this peak is produced by the frontier of the probe laser with lower intensity, we can say that the reflected radiation is amplified around this peak. Through analyzing about the plasma frequency of the REM and the frequency of the probe laser in the electron moving frame, it has found that the two frequencies will be equal at the moment right before the amplification of the reflected radiation occur. So this amplification can be attributed to the resonance between plasma oscillation in the REM and the probe laser in the electron moving frame. Based on this phenomenon, the arriving time of the probe laser can be adjusted in order to selectively amplify or depress the reflected field from REM, leading to the selectively adjusting of the corresponding spectra.
Simulation parameters
To study the generation of the REM and the reflection of the probe laser by the REM, we performed two-dimensional particle-in-cell (2D PIC) simulations using the Vorpal code (Nieter and Cary, Reference Nieter and Cary2004). The schematic drawing of the interaction process is shown in Figure 1. An ultra-intense femtosecond laser pulse normally illuminate on a nanofoil. The electrons in the target are pushed out as a whole electron layer, which forms an REM. During the acceleration of the electron layer, a second probe laser pulse irradiating normally on the layer can be reflected, producing an isolated radiation pulse. The simulation box has a size of 10λ × 20λ in the zx plane, and spatial resolution of 1000 cells/λ both in the z- and x-direction. The main laser is linearly polarized along the x-axis and propagates from the left boundary of the simulation box to right. This pulse has a profile of a 0sin2(πt/T) with pulse duration T = 4λ/c and wavelength λ = 800 nm. The transverse intensity profile is exp( −r 2/R 2), where R = 5λ is the transverse half-width at 1/e 2 of maximum intensity. The normalized laser field a 0 is 100. The counter-propagating probe laser is linearly polarized along the y-axis and propagates from the right boundary of the simulation box to left. The parameters of the counter-propagating probe laser are all the same with the main laser except for the smaller normalized laser field a 0 = 0.1. The smaller intensity can make sure that the REM would not be disturbed distinctly by the probe laser. An ultra-thin nanofoil is used as the target placed perpendicular to the main laser direction. The foil is located at z 1 = 5λ = 4 μm with thickness of d = 2.4 nm. The electron density of the target is n e = 1.315 × 1029 m−3, corresponding to 75n c. n c is the critical density for laser wavelength of 800 nm.

Fig. 1. Schematic drawing of the interaction process in our PIC simulations.
Simulation results and analysis
At two chosen moments 14.7 and 15.4 fs, the spatial distribution of REM and the corresponding radiation field at the same time are shown in Figure 2. Figure 2a and 2c clearly show that the electrons in the REM are accelerated to tens of MeV within less than one femtosecond. The photon energy of the generated radiation is related to the electron energy. For the early time, the smaller electron energy will lead to radiation with longer wavelength. As shown in Figure 2b, the generated radiation field within the area of the REM only contain one half cycle. Then, under higher electron energy, Figure 2d shows that several cycles are contained within the area of the REM. This temporal changing wavelength is the typical feature of chirped pulse. Actually, the generation of the chirped attosecond pulses can also be observed in many previous simulation results (Wu et al., Reference Wu, Meyer-ter-Vehn, Fernández and Hegelich2010; Bulanov et al., Reference Bulanov, Esirkepov, Kando and Koga2016).
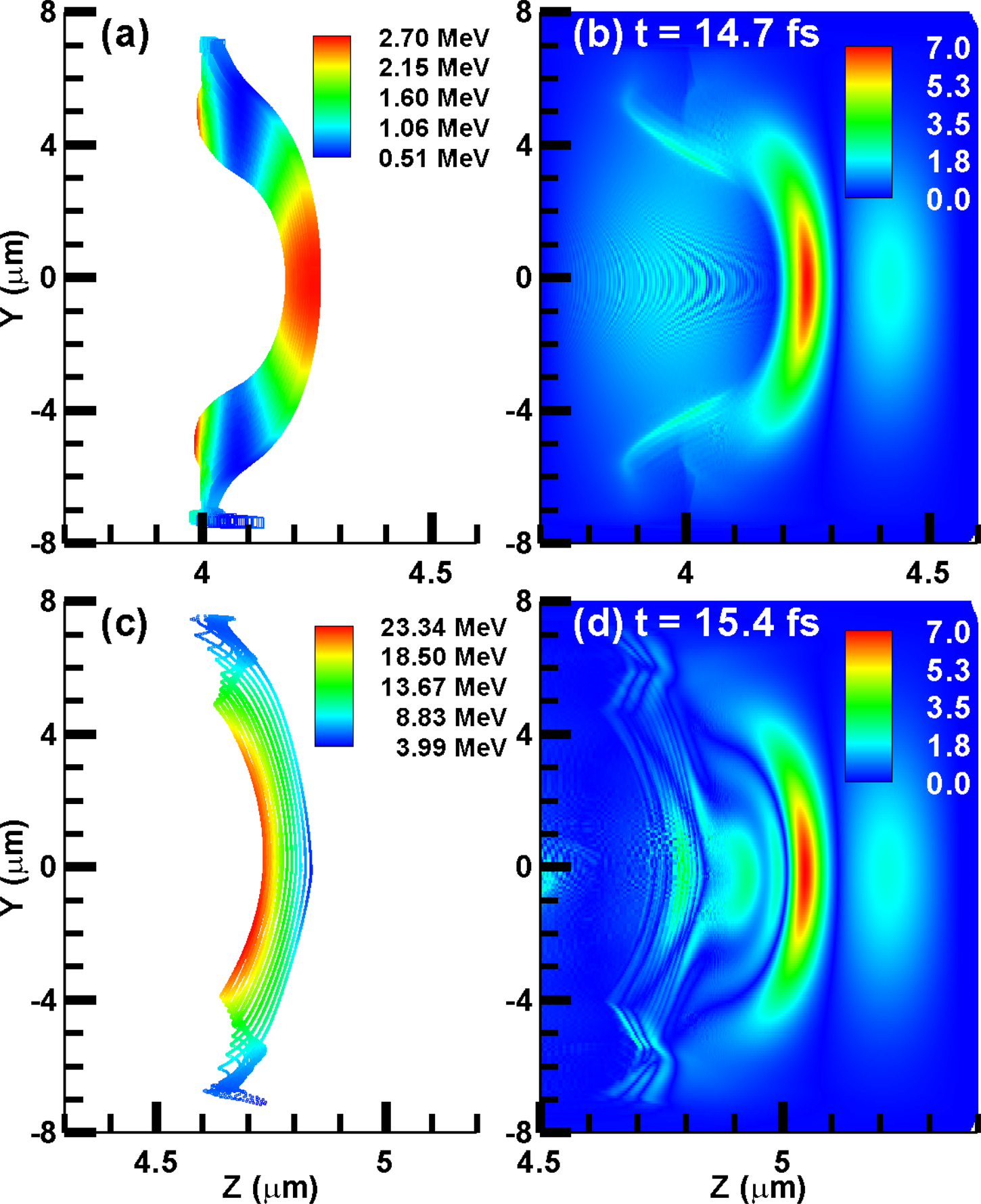
Fig. 2. The spatial distribution for (a,c)the electron layer and (b,d) the generated radiation field at the same time. The first and second row correspond to the results at 14.7 and 15.4 fs, respectively. The unit of the radiation field is 1010 V/m.
In order to analyze the generation process of the reflected radiation, the relation between the reflected field and the corresponding generation moment can be obtained from the simulation results in Figure 3a. In Figure 3a, there is an unusual intense peak right after the moment of 14.21 fs. This peak is generated at the second half cycle of the probe laser, where the peak laser field is four times lower than the maximum laser electric field. So the reflectivity near this peak is obviously amplified. Then, the following emission will be terminated due to the destructive interference when the thickness of the REM becomes larger than half of the wavelength of the generated radiation.
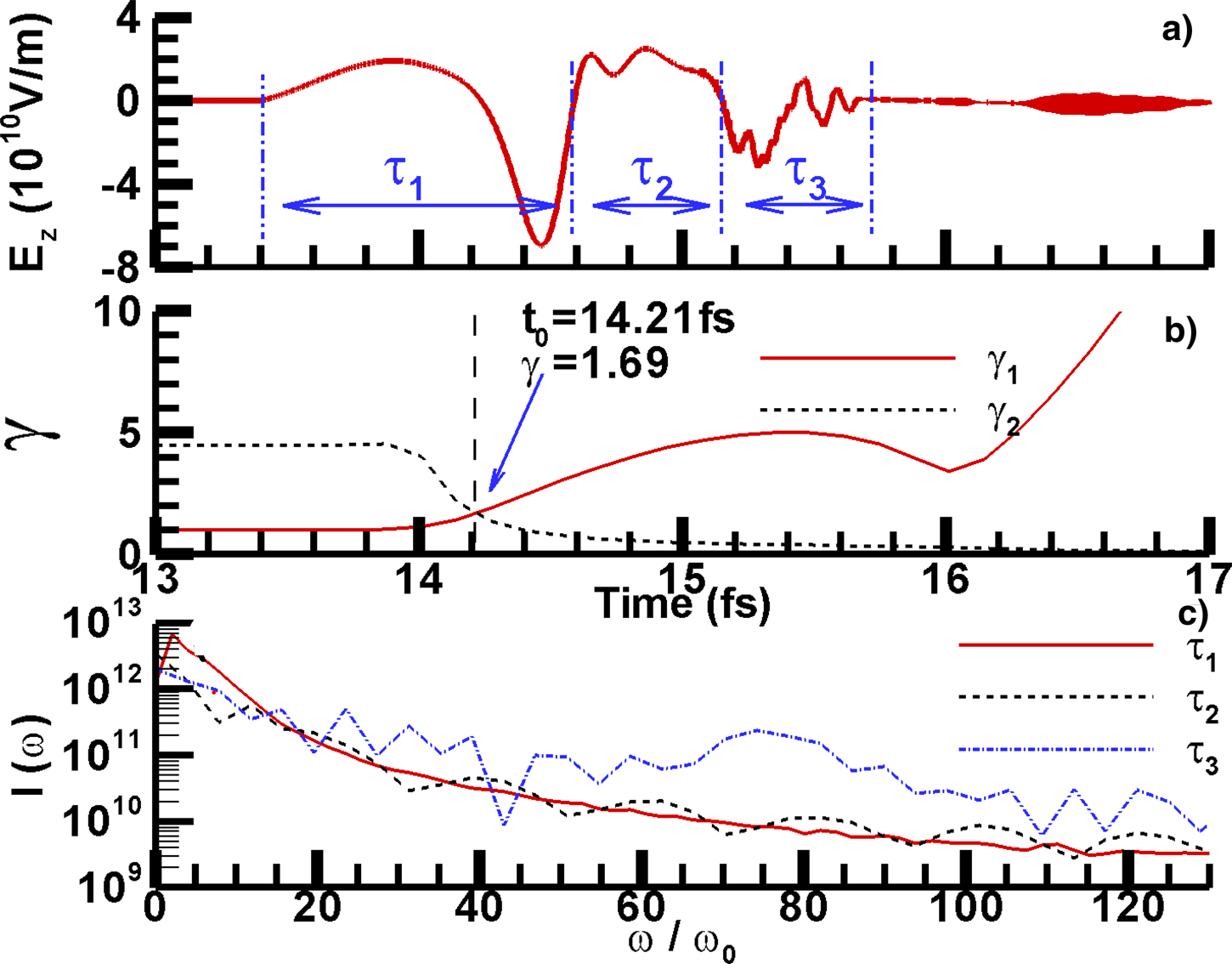
Fig. 3. (a) The relation between the radiation electric field and the corresponding generation moment. The field is divided into three sections which are indicated by the blue dash-dotted lines. (b) The evolution of real energy γ1 (red solid line) and the resonance energy γ2 (black dashed line) of REM. (c) The spectra for the three sections indicated by τ1, τ2, and τ3.
To understanding such unusual amplification, the temporal evolution for the electron energy and density of the REM can be drawn from the simulation results. The plasma frequency of the REM in the lib frame is
where n e(t) is the average electron density in the central part of the REM at different moments, ɛ0 is the permittivity of free space, e is the electron charge, and m e is the electron mass. For the REM with the energy of γ1mc 2, where ![]() ${\rm \gamma }_1 = 1/\sqrt {1-\lpar v_0/c\rpar ^2}$ is the average electron normalized energy and v 0 is the electron velocity. Through the Lorentz transformation from the lab frame of reference to the REM moving frame of reference, the laser frequency
${\rm \gamma }_1 = 1/\sqrt {1-\lpar v_0/c\rpar ^2}$ is the average electron normalized energy and v 0 is the electron velocity. Through the Lorentz transformation from the lab frame of reference to the REM moving frame of reference, the laser frequency ![]() ${\rm \omega}^\prime_{\rm L}$ in the REM moving frame of reference can be obtained as
${\rm \omega}^\prime_{\rm L}$ in the REM moving frame of reference can be obtained as
where ![]() ${\rm \omega} _{\rm L}$ and β = v 0/c is the laser frequency and normalized electron velocity in the lab frame of reference, and k 0 is the laser wave vector.
${\rm \omega} _{\rm L}$ and β = v 0/c is the laser frequency and normalized electron velocity in the lab frame of reference, and k 0 is the laser wave vector.
When ![]() ${\rm \omega}^\prime_{\rm L}$ is equal to the frequency
${\rm \omega}^\prime_{\rm L}$ is equal to the frequency ![]() ${\rm \omega} _{\rm e}$ in the REM moving frame of reference, the resonance between the laser field and the plasma oscillation in the REM can lead to the amplification of reflection. Under the resonance condition, the normalized energy of REM must satisfy the relation of
${\rm \omega} _{\rm e}$ in the REM moving frame of reference, the resonance between the laser field and the plasma oscillation in the REM can lead to the amplification of reflection. Under the resonance condition, the normalized energy of REM must satisfy the relation of
which is determined by the instant density n e(t) and γ1.
The evolution of γ1 and γ2 are shown in Figure 3b. Initially, when the electrons are static, γ1 (t < 13.8 fs) = 1, ![]() ${\rm \omega}^\prime_{\rm L}\lpar t\lt 13.8\, {\rm fs}\rpar = {\rm \omega} _{\rm L}$, and the density n e (t < 13.8 fs) = 75n c ≫ n c. The probe laser is reflected without blue-shift, as the first half cycle shown in Figure 3a. Then, during the acceleration of REM, γ1 keeps increasing and n e keeps decreasing due to the expanding of the REM. According to Eq. (3), γ2 will be reduced due to the increasing of γ1 and the decreasing of n e. The turning point is indicated by the vertically dashed black line both in Figure 3a and 3b at the moment t 0 = 14.21 fs. The two line in Figure 3b intersect at this point. Within a very short time interval right after this moment, the resonance condition between laser field and the plasma oscillation in the REM is satisfied, which will lead to the following amplification of reflection. Then, with the continuously acceleration and expanding of the REM, γ1 will be greater than γ2 after a very short time. So the amplification due to the resonance will be terminated quickly.
${\rm \omega}^\prime_{\rm L}\lpar t\lt 13.8\, {\rm fs}\rpar = {\rm \omega} _{\rm L}$, and the density n e (t < 13.8 fs) = 75n c ≫ n c. The probe laser is reflected without blue-shift, as the first half cycle shown in Figure 3a. Then, during the acceleration of REM, γ1 keeps increasing and n e keeps decreasing due to the expanding of the REM. According to Eq. (3), γ2 will be reduced due to the increasing of γ1 and the decreasing of n e. The turning point is indicated by the vertically dashed black line both in Figure 3a and 3b at the moment t 0 = 14.21 fs. The two line in Figure 3b intersect at this point. Within a very short time interval right after this moment, the resonance condition between laser field and the plasma oscillation in the REM is satisfied, which will lead to the following amplification of reflection. Then, with the continuously acceleration and expanding of the REM, γ1 will be greater than γ2 after a very short time. So the amplification due to the resonance will be terminated quickly.
In order to control and adjust the radiation spectra, it is necessary to analyze the temporal evolution the radiation spectra. The radiation field in Figure 3a can be divided into three sections indicated by τ1, τ2, and τ3. Through Fourier analysis, the spectra for the three sections are, respectively, obtained as the three lines in Figure 3c. For the first section indicated by τ1, the reflected field under the resonance condition is included. The spectrum obtained from Fourier analysis shows that this section mainly contributes to the harmonics of ![]() ${\rm \omega} \lt 10{\rm \omega} _0$. Using the formula,
${\rm \omega} \lt 10{\rm \omega} _0$. Using the formula,
the central radiation frequency γR under the resonance γ of 1.69 is 9.25![]() ${\rm \omega} _{\rm L}$, which is consistent with the results from Fourier analysis. Then, with the acceleration of the REM, the energy of the later generated photons will be higher. The section corresponding to τ3 mainly contributes to the harmonics of
${\rm \omega} _{\rm L}$, which is consistent with the results from Fourier analysis. Then, with the acceleration of the REM, the energy of the later generated photons will be higher. The section corresponding to τ3 mainly contributes to the harmonics of ![]() ${\rm \omega} \gt 20{\rm \omega} _0$, while the contribution of the section corresponding to τ2 is much less than those for τ1 and τ3. The analyses on the temporal evolution the radiation spectra confirm our previous conclusion that the generated radiation is a chirped attosecond pulse. Although the total duration of the chirped pulse is about two femtoseconds, selectively frequency filtering for the spectra can be used to choose certain part of the radiation pulse. So attosecond pulse can be obtained from the selectively frequency filtering.
${\rm \omega} \gt 20{\rm \omega} _0$, while the contribution of the section corresponding to τ2 is much less than those for τ1 and τ3. The analyses on the temporal evolution the radiation spectra confirm our previous conclusion that the generated radiation is a chirped attosecond pulse. Although the total duration of the chirped pulse is about two femtoseconds, selectively frequency filtering for the spectra can be used to choose certain part of the radiation pulse. So attosecond pulse can be obtained from the selectively frequency filtering.
Based on the results in Figure 3b and 3c, one way to control and adjust the radiation spectra can be obtained. Through adjusting the origin position of the probe laser, the relative time delay between the probe laser and the REM can be adjusted. Set the results in Figures 2 and 3 corresponding to the probe laser released at delay 0 μm. The origin position of the probe laser can be adjusted from −0.5 to 2.0 μm. The closer release of the probe laser will make the probe laser reach the REM earlier. The corresponding field and spectra are shown in Figure 4. When the origin position is adjusted from 0 to −0.5 μm, the red solid line in Figure 4 shows that the lower harmonic components (![]() ${\rm \omega} \lt 10{\rm \omega} _0$) are amplified. This amplification can be due to the higher laser field intensity at the resonance moment. Next, when the REM is accelerated to higher energy, the lower laser field intensity will lead to the depression of the higher harmonic components (
${\rm \omega} \lt 10{\rm \omega} _0$) are amplified. This amplification can be due to the higher laser field intensity at the resonance moment. Next, when the REM is accelerated to higher energy, the lower laser field intensity will lead to the depression of the higher harmonic components (![]() ${\rm \omega} \gt 30{\rm \omega} _0$). On the contrary, when the delay is changed from 0.1 to 2.0 μm, the further release of the probe laser will make the probe laser reach the REM later. The laser field intensity at the resonance moment will be lower for the further delay. So the reflected field intensity near the resonance moment and the lower harmonic components (
${\rm \omega} \gt 30{\rm \omega} _0$). On the contrary, when the delay is changed from 0.1 to 2.0 μm, the further release of the probe laser will make the probe laser reach the REM later. The laser field intensity at the resonance moment will be lower for the further delay. So the reflected field intensity near the resonance moment and the lower harmonic components (![]() ${\rm \omega} \lt 30{\rm \omega} _0$) will be depressed. At this condition, the laser field intensity will be higher when the higher harmonic components (
${\rm \omega} \lt 30{\rm \omega} _0$) will be depressed. At this condition, the laser field intensity will be higher when the higher harmonic components (![]() ${\rm \omega} \gt 40{\rm \omega} _0$) are generated. So the higher harmonic components will be amplified.
${\rm \omega} \gt 40{\rm \omega} _0$) are generated. So the higher harmonic components will be amplified.
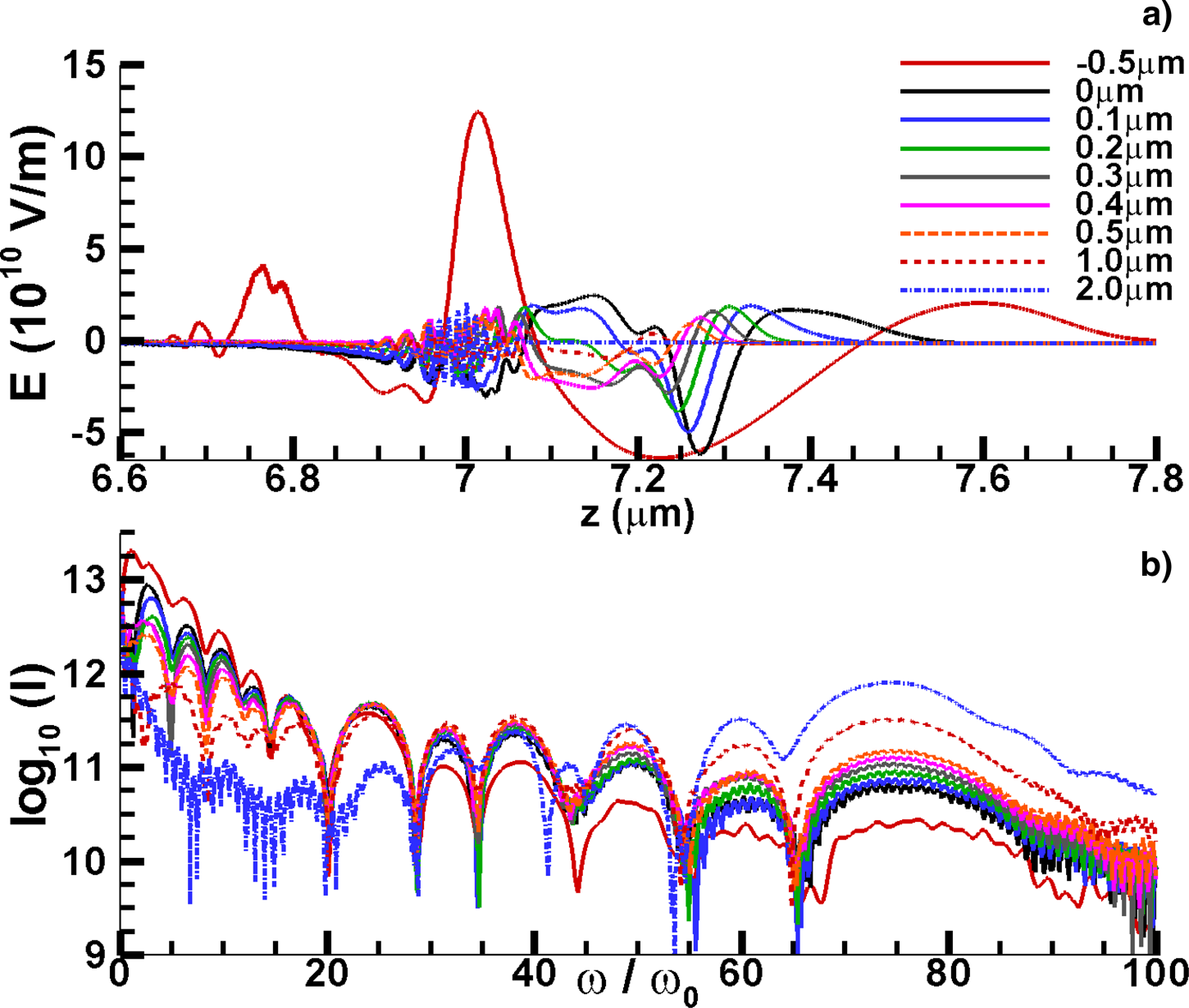
Fig. 4. (a) The reflected field for the different delay of the probe laser. The z position of the result for delay of −0.5 μm is slightly shifted in order to be shown with other results in the same frame. (b) The spectra of the reflected field for the different delay of the probe laser.
Summary and discussion
In conclusion, our numerical studies show that REM with ultra-high acceleration and expanding velocity can be produced from a solid nanofoil illuminated normally by an ultra-intense femtosecond laser pulse with a sharp rising edge. Isolated chirped attosecond pulse can be produced through the reflection of an ultra-short probe laser on the accelerating REM.
The acceleration and expansion of the REM will make the plasma frequency of the REM equal to the frequency of the probe laser in the REM moving frame of reference within an ultra-short time interval. So the reflected radiation near this interval could be obviously amplified due to the resonance between laser field and the plasma oscillation in the REM. The field of the reflected radiation could also be selectively amplified or depressed, through adjusting the arriving time of the probe laser. For the chirped pulse, the controlling of the field will lead to selectively adjusting of the corresponding spectra. Based on the multi-petawatt laser facility in laser Fusion Research Center (Zeng et al., Reference Zeng, Zhou, Zuo, Zhu, Su, Wang, Wang, Huang, Jiang, Jiang, Guo, Xie, Zhou, Wu, Mu, Peng and Jing2017), the corresponding REM generation and radiation experiments can be conducted in our next works.
Acknowledgments
The authors acknowledge a very helpful discussion with Dr. Chuan-Sheng Liu in U. Maryland concerning the exactly solution of electron trajectories. We are also grateful to Dr. Bai-Fei Shen in the Shanghai Institute of Optics and Fine Mechanics, Dr. Wanli Shang in the CAEP, and Dr. Jian Zheng in the USTC for the useful discussions. The authors wish to acknowledge support from the NSAF (Grant No. U1630246), the Presidential Foundation of China Academy of Engineering Physics (Grant No. 2014-1-017), the Science Challenge Program (Project No. TZ2017005), and the National Key R&D Program (Grant No. 2016YFA0401100).






