1. INTRODUCTION
The idea that a laser beam Thomson scattering by relativistic electrons can be a route to bright X-ray generators for use in healthcare, science and industry appeared as early as in the 1990s (Carroll et al., Reference Carroll, Waters, Price, Brau, Roos, Tolk, Pickens and Stephens1990; Sprangle et al., Reference Sprangle, Ting, Esarey and Fisher1992). To increase the X-ray output and efficiency the laser beam is stored in cavity and reused (Sprangle et al., Reference Sprangle, Ting, Esarey and Fisher1992; Glotin et al., Reference Glotin, Ortega, Prazeres, Devanz and Marcouillé1996), with the electrons being provided by a linac (Carroll et al., Reference Carroll, Waters, Price, Brau, Roos, Tolk, Pickens and Stephens1990; Sprangle et al., Reference Sprangle, Ting, Esarey and Fisher1992) or cyclic accelerator (Sprangle et al., Reference Sprangle, Ting, Esarey and Fisher1992; Huang & Ruth, Reference Huang and Ruth1998; Loewen, Reference Loewen2003; Bessonov et al., Reference Bessonov, Vinogradov, Gorbunkov, Tur'yanski, Feshchenko and Shabalin2003). Since the first experimental studies of Thomson X-ray sources built on the basis of dedicated linacs (Carroll, Reference Carroll2002a ; Reference Carroll2002b ; Reference Carroll2003; Carroll et al., Reference Carroll, Mendenhall, Traeger, Brau and Waters2003; Anderson et al., Reference Anderson, Barty, Betts, Brown, Crane, Cross, Fittinghoff, Gibson, Hartemann, Kuba, Lesage, Rosenzweig, Slaughter, Springer and Tremaine2004; Toyokawa et al., Reference Toyokawa, Kuroda, Yasumoto, Sei, Ogawa, Tanaka, Ikeura-Sekiguchi, Koike, Yamada, Sakai, Nakajyo and Yanagida2007) the interest to such kind of X-ray sources grew permanently. These sources are expected to fill the gap existing between conventional X-ray tubes and large accelerator-based facilities with respect to X-beam intensity, tunability, size, power supply, cost, etc. (Bessonov et al., Reference Bessonov, Gorbunkov, Maslova, Kostryukov, Tunkin, Ishkhanov, Shvedunov, Vinogradov, Tallents and Dunn2007, Reference Bessonov, Gorbunkov, Kostryukov, Maslova, Tunkin, Postnov, Mikhailichenko, Shvedunov, Ishkhanov and Vinogradov2009; Gorbunkov et al., Reference Gorbunkov, Maslova and Vinogradov2009). For example, Lyncean Technologies, Inc. (Fremont, CA) offers a “Compact Light Source” – commercial Thomson X-ray generator (TXRG) for production of the photon energies of 10–20 keV. A shortage of compact bright X-ray sources with controllable beam parameters (Sakdinawat & Attwood, Reference Sakdinawat and Attwood2010; Jacquet & Suortti, Reference Jacquet and Suortti2015) has stimulated a number of projects and programs aimed at TXRG development provided by the advances in powerful lasers and high-current accelerators. Some efforts to build an efficient TXRG for various applications are reviewed in Krafft and Priebe (Reference Krafft and Priebe2010), Jacquet (Reference Jacquet2014), Serafini et al. (Reference Serafini, Alesini, Bacci, Bliss, Cassou, Curatolo, Drebot, Dupraz, Giribono, Petrillo, Palumbo, Vaccarezza, Variola and Zomer2016).
The importance of compact tens–hundreds keV X-ray sources for the society is well recognized by Scientific and High-Tech Community. It has stimulated a lot of R&Ds as well as a coordination activity (Assoufid et al., Reference Assoufid, Arp, Naulleau, Biedron and Graves2015). In response to this challenge, this paper presents a concise analysis needed to start the work on design and optimization of a TXRG. Our approach is based on the first principles and enables evaluation, design, and conceptual choice of main TXRG components, including linac, lasers, and photon storage device. The goal can be either a multi-purpose X-ray facility or X-ray source dedicated to a specific application. In the latter case, the X-ray source has to provide the required photon flux within the determined spectral and angular intervals on the illuminated sample area.
A Monte Carlo simulation is known to be a rather effective and accurate method for tracking of the photons toward the sample and recognizing, which of them are acceptable for the specific application. We use this approach to evaluate a potential of linac-based TXRGs for X-ray high-resolution imaging and material analysis of small samples.
Section 2 introduces basic notations and formulas of relativistic Thomson scattering that are required for estimations of the output X-ray flux. Section 3 presents the results of the analysis of two TXRG projects published recently by collaborations in the USA and Japan. Appendix A deduces general formulas of the relativistic Thomson scattering from the first principles, which will be used in the Monte Carlo simulation. A brief description of the developed software is given in Appendix B.
One can find out that Section 2 and Appendixes A and B are sufficient to perform basic analysis, calculation, and design of the TXRG systems, with a tribute being paid to the textbooks Batygin et al. (Reference Batygin, Haar and Toptygin1978), Landau and Lifshits (Reference Landau and Lifshits1975), Pauli (Reference Pauli1933), Sobol (Reference Sobol1994).
2. BASIC FORMULAE
The simplified scheme of the TXRG is shown in Figure 1. It is based on the very well-studied fundamental process – photon–electron scattering. However, this device deals with the collisions of not isolated particles but two bunches (pulses) consisting of up to 1010 electrons and 1017 laser photons, which are controlled to coincide in time and space at the scales of microns and picoseconds. The output X-ray flux, its spectral and angular widths, space structure, and focusability depend crucially on the space and time matching of the colliding bunches and distribution functions of the electrons and photons. Therefore, a design of TXRGs implies an elaboration of the corresponding realistic models for optimization of accelerator, laser and synchronization systems to produce the required flux, spectral width, divergence, etc. of the X-ray beam on a sample.

Fig. 1. Scheme of the TXRG.
The first point in these efforts is an accurate evaluation of the X rays produced by the Thomson scattering of laser pulses on relativistic electron bunches. The related theory can be found in a number of textbooks, original, and review articles. Some useful references are given in Appendix A.
The energies and momentums acquired by isolated particles in elastic collisions obey energy and momentum conservation laws. The energy of laser photon scattered by moving electron equals to (see Batygin et al., Reference Batygin, Haar and Toptygin1978):
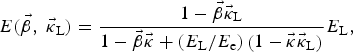 $$E({\rm \vec {\rm \beta}}, \;{\rm \vec {\rm \kappa}} _{\rm L}) = \displaystyle{{1 - {\rm \vec {\rm \beta}} {{\rm \vec {\rm \kappa}}} _{\rm L}} \over {1 - {\rm \vec {\rm \beta} \vec {\rm \kappa}} + (E_{\rm L}/E_{\rm e})\left( {1 - {\rm \vec {\rm \kappa}} {{\rm \vec {\rm \kappa}}} _{\rm L}} \right)}}E_{\rm L},$$
$$E({\rm \vec {\rm \beta}}, \;{\rm \vec {\rm \kappa}} _{\rm L}) = \displaystyle{{1 - {\rm \vec {\rm \beta}} {{\rm \vec {\rm \kappa}}} _{\rm L}} \over {1 - {\rm \vec {\rm \beta} \vec {\rm \kappa}} + (E_{\rm L}/E_{\rm e})\left( {1 - {\rm \vec {\rm \kappa}} {{\rm \vec {\rm \kappa}}} _{\rm L}} \right)}}E_{\rm L},$$
where E
e and E
L = ћωL are the electron and laser photon energies,
![]() $\vec p = m\vec v{\rm \gamma} $
and
$\vec p = m\vec v{\rm \gamma} $
and
![]() $\hbar \vec k_{\rm L}$
are the momentums of colliding electron and photon,
$\hbar \vec k_{\rm L}$
are the momentums of colliding electron and photon,
![]() ${\rm \vec {\rm \kappa}} $
and
${\rm \vec {\rm \kappa}} $
and
![]() ${\rm \vec {\rm \kappa}} _{\rm L}$
are the unit vectors defining directions of laser and scattered X-ray photons,
${\rm \vec {\rm \kappa}} _{\rm L}$
are the unit vectors defining directions of laser and scattered X-ray photons,
![]() $\vec v = c{\rm \vec {\rm \beta}} $
is the incident electron velocity, and γ is the relativistic factor. The Thomson and Compton scatterings are distinguished by the value of the parameter 4γћωL/mc
2 ≪ 1. Evidently, an effective conversion of laser radiation to the X rays is provided in the case of relativistic (γ ≫ 1) counter collisions with
$\vec v = c{\rm \vec {\rm \beta}} $
is the incident electron velocity, and γ is the relativistic factor. The Thomson and Compton scatterings are distinguished by the value of the parameter 4γћωL/mc
2 ≪ 1. Evidently, an effective conversion of laser radiation to the X rays is provided in the case of relativistic (γ ≫ 1) counter collisions with
![]() ${\rm \vec {\rm \beta} \vec {\rm \kappa}} \approx - {\rm \vec {\rm \kappa}} {\rm \vec {\rm \kappa}} _{\rm L} \approx 1$
. Then the energy of the scattered photon (1) can be rewritten as:
${\rm \vec {\rm \beta} \vec {\rm \kappa}} \approx - {\rm \vec {\rm \kappa}} {\rm \vec {\rm \kappa}} _{\rm L} \approx 1$
. Then the energy of the scattered photon (1) can be rewritten as:
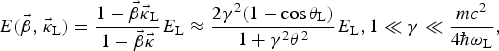 $$\eqalign{& E({\rm \vec {\rm \beta},} \;{{\rm \vec {\rm \kappa}}} _{\rm L}) = \displaystyle{{1 - {\rm \vec {\rm \beta}} {{\rm \vec {\rm \kappa}}} _{\rm L}} \over {1 - {\rm \vec {\rm \beta} \vec {\rm \kappa}}}} E_{\rm L} \approx \displaystyle{{2{\rm \gamma} ^2(1 - \cos {\rm \theta} _{\rm L})} \over {1 + {\rm \gamma} ^2{\rm \theta} ^2}}E_{\rm L}, 1 \ll {\rm \gamma} \ll \displaystyle{{mc^2} \over {4\hbar {\rm \omega} _{\rm L}}},} $$
$$\eqalign{& E({\rm \vec {\rm \beta},} \;{{\rm \vec {\rm \kappa}}} _{\rm L}) = \displaystyle{{1 - {\rm \vec {\rm \beta}} {{\rm \vec {\rm \kappa}}} _{\rm L}} \over {1 - {\rm \vec {\rm \beta} \vec {\rm \kappa}}}} E_{\rm L} \approx \displaystyle{{2{\rm \gamma} ^2(1 - \cos {\rm \theta} _{\rm L})} \over {1 + {\rm \gamma} ^2{\rm \theta} ^2}}E_{\rm L}, 1 \ll {\rm \gamma} \ll \displaystyle{{mc^2} \over {4\hbar {\rm \omega} _{\rm L}}},} $$
where θL and θ are the angles of laser and scattered X-ray photons with respect to the electron velocity. One can see that formula (2) can be used for preliminary analysis of TXRG properties. Thus, the maximum X-ray photon energy E m = 4γ2 E L is achieved in the backscattering with head-on-collisions, when cosθL = −1 and γ2θ2 ≪ 1.
In the case of fixed geometry of the collisions (i.e.
![]() ${\rm \vec {\rm \beta}} $
and
${\rm \vec {\rm \beta}} $
and
![]() ${\rm \vec {\rm \kappa}} _{\rm L}$
are fixed) the energy E of the scattered photon is defined by its direction
${\rm \vec {\rm \kappa}} _{\rm L}$
are fixed) the energy E of the scattered photon is defined by its direction
![]() ${\rm \vec {\rm \kappa}} $
. This fact gives a possibility to obtain a monochromatization of the TXRG output spectra by using a properly positioned slit or pinhole. Formula (2) gives an angle θ at which the X-ray photons of energy E can be filtered out in such a way:
${\rm \vec {\rm \kappa}} $
. This fact gives a possibility to obtain a monochromatization of the TXRG output spectra by using a properly positioned slit or pinhole. Formula (2) gives an angle θ at which the X-ray photons of energy E can be filtered out in such a way:
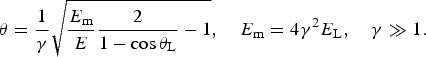 $${\rm \theta} = \displaystyle{1 \over {\rm \gamma}} \sqrt {\displaystyle{{E_{\rm m}} \over E}\displaystyle{2 \over {1 - \cos {\rm \theta} _{\rm L}}} - 1}, \quad E_{\rm m} = 4{\rm \gamma} ^2E_{\rm L},\quad {\rm \gamma} \gg 1.$$
$${\rm \theta} = \displaystyle{1 \over {\rm \gamma}} \sqrt {\displaystyle{{E_{\rm m}} \over E}\displaystyle{2 \over {1 - \cos {\rm \theta} _{\rm L}}} - 1}, \quad E_{\rm m} = 4{\rm \gamma} ^2E_{\rm L},\quad {\rm \gamma} \gg 1.$$
Note that the effects related to the momentum spread in the colliding beams are rather important and they can be estimated with Eq. (2) as well as Jacquet (Reference Jacquet2014).
To handle the particle momentums distribution rigorously we will use the following expression for the average flux Φ of the specified X-ray photons (e.g. within the determined ranges of the energy and angle):
As was earlier considered in Bessonov et al. (Reference Bessonov, Gorbunkov, Maslova, Kostryukov, Tunkin, Ishkhanov, Shvedunov, Vinogradov, Tallents and Dunn2007), formula (4) implies that electrons entering the TXRG (see Fig. 1) are grouped in the trains of n e bunches containing N e particles each. These bunch trains are produced by the RF gun with a rate of v e, an average current of I, and accelerated up to tens of MeV energy by linear accelerator (linac). Then every e-bunch collides with a stored (or accumulated) pulse of N s L = η N L laser photons within the photon storage device, where η is the coupling factor and N L is the amount of photons in the incoming laser pulse. The X rays are generated in a sequence of similar trains of n e pulses with N photons each. The last factor in Eq. (4) W is the reduced yield (RY) that is the number of given photons produced in one act of e-bunch – laser pulse collision reduced to one pair of the colliding particles. Evidently the RY value W depends on the particle distribution functions of e-bunches and laser pulses as well as the differential scattering cross-section of the colliding particles. Appendixes A and B present the explicit formulas and Monte Carlo numerical approach, correspondingly, for a calculation of the value of W. It should be noted that RY does not depend on the number of particles N e and N L in the colliding beams.
The coupling factor η in Eq. (4) is determined by the optical storage device used. In this paper, we consider a coherent power enhancement cavity (Sprangle et al., Reference Sprangle, Ting, Esarey and Fisher1992; Carstens et al., Reference Carstens, Lilienfein, Holzberger, Jocher, Eidam, Limpert, Tünnermann, Weitenberg, Yost, Alghamdi, Alahmed, Azzeer, Apolonski, Fill, Krausz and Pupeza2014) or a circulator with intracavity second-harmonic generation (Bessonov et al., Reference Bessonov, Gorbunkov, Maslova, Kostryukov, Tunkin, Ishkhanov, Shvedunov, Vinogradov, Tallents and Dunn2007; Jovanovic et al., Reference Jovanovic, Shverdin, Gibson and Brown2007), which have different ratios of the photon numbers inside the storage device and the pump laser: typically η ≈ 103 for power enhancement cavity and η ≈ 0.25 for second-harmonic circulator.
The output X-ray flux (4) can be easily evaluated by introducing the average linac current I = eN
e
n
eνe and pump laser pulse energy
![]() $E_{\rm L} = N_{\rm L}\hbar {\rm \omega} _{\rm L}$
:
$E_{\rm L} = N_{\rm L}\hbar {\rm \omega} _{\rm L}$
:
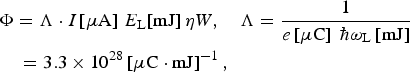 $$\eqalign{& \Phi = \Lambda \cdot I{\kern 1pt} [{\rm \mu A}]\;E_{\rm L}[{\rm mJ}]\,{\rm \eta} W,\quad \Lambda = \displaystyle{1 \over {e\left[ {{\rm \mu C}} \right]\;\hbar {\rm \omega} _{\rm L}\left[ {{\rm mJ}} \right]}} \cr & \quad = 3.3 \times 10^{28}\left[ {{\rm \mu C} \cdot {\rm mJ}} \right]^{ - 1},} $$
$$\eqalign{& \Phi = \Lambda \cdot I{\kern 1pt} [{\rm \mu A}]\;E_{\rm L}[{\rm mJ}]\,{\rm \eta} W,\quad \Lambda = \displaystyle{1 \over {e\left[ {{\rm \mu C}} \right]\;\hbar {\rm \omega} _{\rm L}\left[ {{\rm mJ}} \right]}} \cr & \quad = 3.3 \times 10^{28}\left[ {{\rm \mu C} \cdot {\rm mJ}} \right]^{ - 1},} $$
where the value of Λ is determined by the laser wavelength λL (for Yb:YAG laser λL = 1.03 µm, ћωL = 1.2 eV).
Two parameters – the repetition rates νe and νL of linac and laser – are absent in Eq. (5) but still important for overall system design analysis because they specify the required power of the driving laser and RF gun. The photon storage revolution rate is limited by νs = τs −1 ≤ 150 MHz and the RF gun by νe ≤ 1 kHz (without superconductive technologies).
In the next section, we will apply the described the above approach and formulas to review the prospects of linac-based TXRGs.
3. ANALYSIS OF TXRG DESIGN PARAMETERS
As was mentioned in Section 1, the main goal of a TXRG development is to fill up the empty space between large synchrotron radiation facilities and conventional X-ray sources from the viewpoint of construction and operational costs, compactness and flux. Keeping this in mind, we will consider examples of an implementation of two recently reported compact accelerators Shimizu et al. (Reference Shimizu, Akemoto, Arai, Araki, Aryshev, Fukuda, Fukuda, Haba, Hara, Hayano, Higashi, Honda, Honma, Kako, Kojima, Kondo, Lekomtsev, Matsumoto, Michizono, Miyoshi, Nakai, Nakajima, Nakanishi, Noguchi, Okugi, Sato, Shevelev, Shishido, Takenaka, Tsuchiya, Urakawa, Watanabe, Yamaguchi, Yamamoto, Yamamoto, Sakaue, Hosoda, Iijima, Kuriki, Tanaka, Kuramoto, Omet and Takeda2015) and Graves et al. (Reference Graves, Bessuille, Brown, Carbajo, Dolgashev, Hong, Ihloff, Khaykovich, Lin, Murari, Nanni, Resta, Tantawi, Zapata, Kärtner and Moncton2014) in the TXRGs for X-ray imaging or microanalysis. This review can show how far we are from the stated objective and indicate main directions and bottlenecks of the TXRG development.
Table 1 presents the parameters and simulation results (in last four columns) for two versions of linac-based laser–electron X-ray generators marked as TXRG1 and TXRG2, with the RF gun and accelerator being taken from Shimizu et al. (Reference Shimizu, Akemoto, Arai, Araki, Aryshev, Fukuda, Fukuda, Haba, Hara, Hayano, Higashi, Honda, Honma, Kako, Kojima, Kondo, Lekomtsev, Matsumoto, Michizono, Miyoshi, Nakai, Nakajima, Nakanishi, Noguchi, Okugi, Sato, Shevelev, Shishido, Takenaka, Tsuchiya, Urakawa, Watanabe, Yamaguchi, Yamamoto, Yamamoto, Sakaue, Hosoda, Iijima, Kuriki, Tanaka, Kuramoto, Omet and Takeda2015) and Graves et al. (Reference Graves, Bessuille, Brown, Carbajo, Dolgashev, Hong, Ihloff, Khaykovich, Lin, Murari, Nanni, Resta, Tantawi, Zapata, Kärtner and Moncton2014), correspondingly. Characteristics of the driving laser and photon storage device were obtained on the basis of the state-of-the-art and emerging laser and optical technologies.
Table 1. Total and quasi-monochromatic X-ray photon fluxes ΦT, ΦM and corresponding RYs W T and W M calculated for two different versions TXRG1 (Shimizu et al., Reference Shimizu, Akemoto, Arai, Araki, Aryshev, Fukuda, Fukuda, Haba, Hara, Hayano, Higashi, Honda, Honma, Kako, Kojima, Kondo, Lekomtsev, Matsumoto, Michizono, Miyoshi, Nakai, Nakajima, Nakanishi, Noguchi, Okugi, Sato, Shevelev, Shishido, Takenaka, Tsuchiya, Urakawa, Watanabe, Yamaguchi, Yamamoto, Yamamoto, Sakaue, Hosoda, Iijima, Kuriki, Tanaka, Kuramoto, Omet and Takeda2015) and TXRG2 (Graves et al., Reference Graves, Bessuille, Brown, Carbajo, Dolgashev, Hong, Ihloff, Khaykovich, Lin, Murari, Nanni, Resta, Tantawi, Zapata, Kärtner and Moncton2014) of linac-based laser–electron X-ray generators: E is the energy of the X-ray photons, E e is the energy of the electrons, I is the averaged current of the RF gun, εn is the normalized electron emittance, σe is the size of the electron beam waist, λL is the laser wavelength, σL is the size of the laser beam waist, E L is the energy of the laser pulse, W T, W M are the RYs corresponding to the total and quasi-monochromatic fluxes, and ΦT, ΦM are the total and quasi-monochromatic fluxes. Underlined values indicate design parameters taken from the corresponding publication

Note that estimation of the X-ray photon flux and parameter RY in Eq. (5) supposes the definition of the spectra according to a specific application. Thus, X-ray imaging technologies such as radiography or tomography deals with the wide X-ray spectra and beam divergence, whereas a microanalysis study such as X-ray diffraction (XRD) does with monochromatic and collimated beams. We calculated two values: total photon flux ΦT, which is important for an X-ray imaging and photon flux ΦM limited by the narrow spectral interval dE/E = 10−3, which is important for microanalysis applications. According to Eq. (5) the fluxes ΦT and ΦM are proportional to RYs W T and W M. The corresponding values were calculated in here with the help of Monte Carlo simulations described in Appendix B.
There is an essential difference between TXRG1 and TXRG2. First of all, the IR-driving lasers operate in different modes: continuous (162.5 MHz) in TXRG1 and pulsed (1 kHz) in TXRG2. Then, they use different types of the photon storage device: TXRG1 incorporates a power enhancement cavity with the coupling factor η = 1.5×103, TXRG2 does an optical circulator with the coupling factor η = 0.25 in TXRG2. The average laser power values are estimated to be about 1.5 kW (CW) for TXRG1 and 100 W (pulsed) for TXRG2, that is, both laser systems are within the reach of modern laser technology (Carstens et al., Reference Carstens, Lilienfein, Holzberger, Jocher, Eidam, Limpert, Tünnermann, Weitenberg, Yost, Alghamdi, Alahmed, Azzeer, Apolonski, Fill, Krausz and Pupeza2014; Fattahi et al., Reference Fattahi, Barros, Gorjan, Nubbemeyer, Alsaif, Teisset, Schultze, Prinz, Haefner, Ueffing, Alismail, Vámos, Schwarz, Pronin, Brons, Geng, Arisholm, Ciappina, Yakovlev, Kim, Azzeer, Karpowicz, Sutter, Major, Metzger and Krausz2014; Graves et al., Reference Graves, Bessuille, Brown, Carbajo, Dolgashev, Hong, Ihloff, Khaykovich, Lin, Murari, Nanni, Resta, Tantawi, Zapata, Kärtner and Moncton2014; Reagan et al., Reference Reagan, Berrill, Wernsing, Baumgarten, Woolston and Rocca2014).
The predicted total flux ΦT (see Table 1) exceeds by 20–80 times the requirements of phase-contrast tomography experiments with a TXRG-type source (Eggl et al., Reference Eggl, Schleede, Bech, Achterhold, Loewen, Ruth and Pfeiffer2015). It is necessary to note here that TXRG used in the cited work Eggl et al. (Reference Eggl, Schleede, Bech, Achterhold, Loewen, Ruth and Pfeiffer2015) was a more complicated system of a greater size, since it included a tens MeV storage ring in addition to the linac. The high-flux value is attributable to a smaller size of the electron–photon interaction region.
The technical applicability of the TXRG for XRD measurements is determined by the divergence of its output X-ray beam. This parameter can be obtained from the electron and photon distribution functions with the help of the theoretical approach presented in Appendix A, but here we will confine ourselves with a more simple estimation on the base of Eq. (3). This equation allows one to take into account the given angular and energy spread of the electron and laser beams. Then the X-ray divergence δθ resulted from the e-beam energy spread δγ/γ can be estimated as:
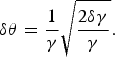 $${\rm \delta} {\rm \theta} = \displaystyle{1 \over {\rm \gamma}} \sqrt {\displaystyle{{2{\rm \delta} {\rm \gamma}} \over {\rm \gamma}}}. $$
$${\rm \delta} {\rm \theta} = \displaystyle{1 \over {\rm \gamma}} \sqrt {\displaystyle{{2{\rm \delta} {\rm \gamma}} \over {\rm \gamma}}}. $$
In further calculations, we will adopt δγ/γ = 1% for both examples: TXRG1 (γ = 78) and TXRG2 (γ = 35).
Microanalysis (e.g. XRD) applications determine the flux Φ1 and beam divergence δθ1 on a sample of small size (diameter) σ1. The energy and brightness conservation laws establish the following relation between the final flux Φ1 incident onto sample and the initial flux Φ, given the ideal optics with 100% throughput:
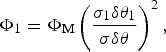 $$\Phi _1 = \Phi _{\rm M}\left( {\displaystyle{{{\rm \sigma} _1 {\rm \delta} {\rm \theta} _1} \over {{\rm \sigma} {\rm \delta} {\rm \theta}}}} \right)^2,$$
$$\Phi _1 = \Phi _{\rm M}\left( {\displaystyle{{{\rm \sigma} _1 {\rm \delta} {\rm \theta} _1} \over {{\rm \sigma} {\rm \delta} {\rm \theta}}}} \right)^2,$$
where we use ΦM instead of ΦT as the flux under consideration is limited by the narrow spectral interval dE/E ≈ 10−3, and the source size is σ ≈ σe ≈ σL. With using formulas (6) and (7) and Table 1 one can calculate the X-ray flux produced by either TXRG1 or TXRG2 on a sample of given size σ1 with the divergence δθ1. For σ1 ≈ 10 µm and δθ1 ≈ 10−3 the calculations result in Φ1 = 2 × 109 ph/s for TXRG1 and Φ1 = 2.4 × 1010 ph/s for TXRG2. For comparison, the X-ray beamline for high pressure research at Advanced Photon Source (Shen et al., Reference Shen, Prakapenka, Eng, Rivers and Sutton2005) provides Φ1 = 5·108–5 × 1011 ph/s with the same experimental parameters, with the diffraction collecting time being from a few seconds to minutes. We expect that a proper application of X-ray optics can reduce the gap between the flux values of synchrotron and TXRG to enable an operative recording of XRD data in homelabs, at least, with ~1 h exposure.
4. SUMMARY
For general analysis of linac-based Thomson scattering X-ray generators (TXRG) we put together the first principles formulas for the rates of elementary processes in collisions of relativistic particles (Landau & Lifshits, Reference Landau and Lifshits1975) and Monte Carlo method in the standard version of statistical tests (Sobol, Reference Sobol1994). The photon flux of TXRG in a certain phase volume can be easily estimated by using formula (5) in terms of the average linac current I, driving laser pulse energy E L and reduced photon yield W (per one electron–photon pair). We introduced the reduced photon yield W parameter which has been proven to accumulate the influence of all (ten or more, see Appendices A and B) the parameters characterizing the colliding electron and photon beams: emittance, the Raleigh length, beam sizes in the interaction point, angular and energy spread, etc. The version of Thomson scattering theory presented is complete and concise due to direct footing on the basic principles of relativistic mechanics (Landau & Lifshits, Reference Landau and Lifshits1975).
The results of the study show that existing front edge and projected kW-scale picosecond lasers and 30–60 MeV accelerators allow for construction of high X-ray flux “homelab” sources for the experiments, which currently can be conducted only in big X-ray science centers based on electron storage rings, for example. synchrotrons. The presented approach can be used for designing, further elaboration and optimization of TXRGs as new equipment easily accessible for many applications in science, healthcare, and education (Assoufid et al., Reference Assoufid, Arp, Naulleau, Biedron and Graves2015).
ACKNOWLEDGEMENTS
This work was supported by the program of fundamental investigations of the Russian Academy of Science Presidium “Fundamental and applied problems of photonics and physics of new optical materials”. The authors are grateful to B.S. Ishkhanov, V.I. Shvedunov, R.M. Feshchenko, S.L. Vinogradov, and A.S. Busarov for helpful discussions and reading the manuscript.
APPENDIX A
A1. USEFUL FORMULAS FOR THE THOMSON SCATTERING GENERATORS
A1.1. Number of collisions and the RY
For the sake of completeness, we present here the theory and formulas needed for calculation of the X-ray spectra resulted from a collision of relativistic e-bunch with the laser pulse.
Accurate simulation of the number of reactions in crossing beams is known to require the particle distribution function in phase space. We will solve this problem using the standard approach of the classical field theory (Landau & Lifshits, Reference Landau and Lifshits1975) introduced by W. Pauli (Pauli, Reference Pauli1933), which is the shortest way to the result. Another approach and more formulas can be found in papers [Hartemann et al. (Reference Hartemann, Brown, Gibson, Anderson, Tremaine, Springer, Wootton, Hartouni and Barty2005), Sun and Wu (Reference Sun and Wu2011) and references therein].
The number of events in a volume
![]() ${\rm d}\vec r$
for the period dt caused by electron–photon collisions with the momentum
${\rm d}\vec r$
for the period dt caused by electron–photon collisions with the momentum
![]() $\vec p = m\vec v{\rm \gamma} = mc{\rm \gamma} \vec {\rm \beta} $
and k-vector
$\vec p = m\vec v{\rm \gamma} = mc{\rm \gamma} \vec {\rm \beta} $
and k-vector
![]() $\vec k_{\rm L} = k_{\rm L}{\rm \vec {\rm \kappa}} _{\rm L}$
(see Fig. 2) is:
$\vec k_{\rm L} = k_{\rm L}{\rm \vec {\rm \kappa}} _{\rm L}$
(see Fig. 2) is:
![]() $n_{\rm e}(\vec r,t)$
and
$n_{\rm e}(\vec r,t)$
and
![]() $\;n_{\rm L}(\vec r,t)$
are the electron and laser photon densities,
$\;n_{\rm L}(\vec r,t)$
are the electron and laser photon densities,
![]() $\vec v$
is the laboratory frame electron velocity, and [dσ]′ is the cross-section of given event in the electron rest frame S′.
$\vec v$
is the laboratory frame electron velocity, and [dσ]′ is the cross-section of given event in the electron rest frame S′.
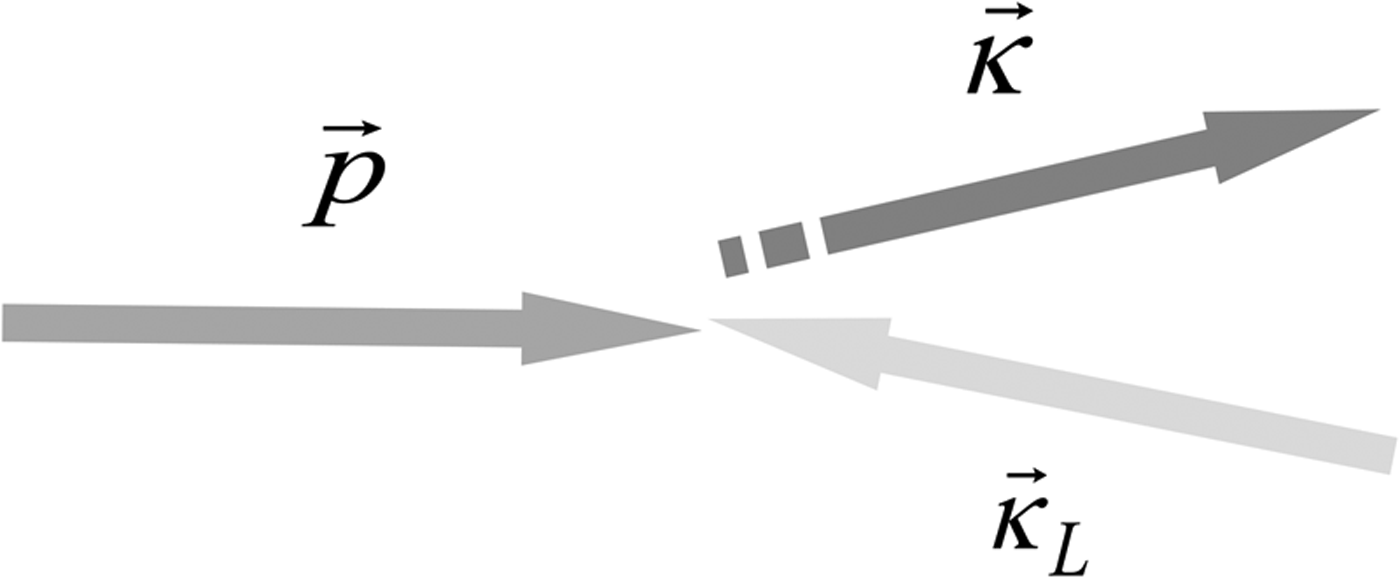
Fig. 2. Geometry of the Thomson scattering:
![]() $\vec p$
is the electron momentum,
$\vec p$
is the electron momentum,
![]() ${\rm \vec {\rm \kappa}} _{\rm L}$
and
${\rm \vec {\rm \kappa}} _{\rm L}$
and
![]() ${\rm \vec {\rm \kappa}} $
are the unit vectors of incident (laser) and scattered (X ray) photon k-vectors.
${\rm \vec {\rm \kappa}} $
are the unit vectors of incident (laser) and scattered (X ray) photon k-vectors.
Then the act of a laser photon scattering in the direction
![]() ${\rm \vec {\rm \kappa}} $
in a solid angle of dΩ can be described as:
${\rm \vec {\rm \kappa}} $
in a solid angle of dΩ can be described as:
with
![]() $ {\vec {\rm \kappa} ^{\,\prime}},{\rm d{\Omega} ^{\prime}},{\vec p}^{\,\prime},{\vec k}^{\,\prime}_{\rm L},{\vec k}^{\,\prime}$
are the scattered X-ray photon angles
$ {\vec {\rm \kappa} ^{\,\prime}},{\rm d{\Omega} ^{\prime}},{\vec p}^{\,\prime},{\vec k}^{\,\prime}_{\rm L},{\vec k}^{\,\prime}$
are the scattered X-ray photon angles
![]() ${\rm \vec {\rm \kappa}}, \,{\rm d\Omega} $
, electron momentum
${\rm \vec {\rm \kappa}}, \,{\rm d\Omega} $
, electron momentum
![]() $\vec p$
, laser photon k-vector
$\vec p$
, laser photon k-vector
![]() $\vec k_{\rm L}$
and scattered X-ray photon k-vector
$\vec k_{\rm L}$
and scattered X-ray photon k-vector
![]() $\vec k$
written in the moving reference frame S′. Taking into account (A2) the number of events (A1), that is the number of X-ray photons generated in the direction
$\vec k$
written in the moving reference frame S′. Taking into account (A2) the number of events (A1), that is the number of X-ray photons generated in the direction
![]() ${\rm \vec {\rm \kappa}} $
and solid angle dΩ, takes the form:
${\rm \vec {\rm \kappa}} $
and solid angle dΩ, takes the form:
with the well-known expressions for the Jacobian and Thomson cross-section (Batygin et al., Reference Batygin, Haar and Toptygin1978):
 $$\eqalign{ \displaystyle{{{\rm d}{\Omega} ^{\prime}} \over {{\rm d}\Omega}} &= \displaystyle{{\rm 1} \over {{\rm \gamma} ^2{(1 - {\rm \vec {\rm \beta} \vec {\rm \kappa}} )}^2}},\quad \displaystyle{{{\rm d{\rm \sigma}} ({\vec {\rm \kappa} ^{\,\prime}})} \over {{\rm d}{\Omega} ^{\prime}}} = {\rm \sigma} _{{\rm Th}}(\vec p,{{\rm \vec {\rm \kappa}}} _{\rm L}{\rm, \vec {\rm \kappa} )} = \displaystyle{{1 + {({{\vec {\rm \kappa} ^{\,\prime}}}_{\rm L} {\vec {\rm \kappa} ^{\,\prime}})}^2} \over 2}r_0^2, \cr r_0 &= \displaystyle{{e^2} \over {mc^2}}, {\vec {\rm \kappa}}_{\rm L}^{\,\prime} {{\mathop {\kappa} ^{\hskip-5pt\leftarrow}}^{\prime}} = 1 - \displaystyle{{1 - {{\rm \vec {\rm \kappa}}} _{\rm L}{\rm \vec {\rm \kappa}}} \over {{\rm \gamma} ^2(1 - {\rm \vec {\rm \beta} \vec {\rm \kappa}} ) \;(1 - {\rm \vec {\rm \beta}} {{\rm \vec {\rm \kappa}}}_{\rm L})}}.}$$
$$\eqalign{ \displaystyle{{{\rm d}{\Omega} ^{\prime}} \over {{\rm d}\Omega}} &= \displaystyle{{\rm 1} \over {{\rm \gamma} ^2{(1 - {\rm \vec {\rm \beta} \vec {\rm \kappa}} )}^2}},\quad \displaystyle{{{\rm d{\rm \sigma}} ({\vec {\rm \kappa} ^{\,\prime}})} \over {{\rm d}{\Omega} ^{\prime}}} = {\rm \sigma} _{{\rm Th}}(\vec p,{{\rm \vec {\rm \kappa}}} _{\rm L}{\rm, \vec {\rm \kappa} )} = \displaystyle{{1 + {({{\vec {\rm \kappa} ^{\,\prime}}}_{\rm L} {\vec {\rm \kappa} ^{\,\prime}})}^2} \over 2}r_0^2, \cr r_0 &= \displaystyle{{e^2} \over {mc^2}}, {\vec {\rm \kappa}}_{\rm L}^{\,\prime} {{\mathop {\kappa} ^{\hskip-5pt\leftarrow}}^{\prime}} = 1 - \displaystyle{{1 - {{\rm \vec {\rm \kappa}}} _{\rm L}{\rm \vec {\rm \kappa}}} \over {{\rm \gamma} ^2(1 - {\rm \vec {\rm \beta} \vec {\rm \kappa}} ) \;(1 - {\rm \vec {\rm \beta}} {{\rm \vec {\rm \kappa}}}_{\rm L})}}.}$$
Formulas (A3) and (A4) provide a theoretical basis for calculation and characterization of X-ray radiation produced by a scattering of laser pulse on electron bunch. For example, total number of the events in one e-bunch – laser pulse collision can be found by integrating of (A3) over space and time to produce:
where W is the RY, defined as the number of events under consideration per one pair of the colliding particles:
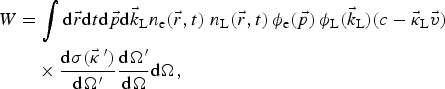 $$\eqalign{ W &= \int {{\rm d}\vec r{\rm d}t{\rm d}\vec p{\rm d}{\vec k}_{\rm L}n_{\rm e}(\vec r,t){\kern 1pt} \,n_{\rm L}(\vec r,t)\,{\rm \phi} _{\rm e}(\vec p)\,{\rm \phi} _{\rm L}({\vec k}_{\rm L})(c - {{\rm \vec {\rm \kappa}}} _{\rm L}\vec v)} \cr & \quad \times\displaystyle{{{\rm d \sigma} ({\vec {\rm \kappa} ^{\,\prime}})} \over {{\rm d}{\Omega} ^{\prime}}}\displaystyle{{{\rm d}{\Omega} ^{\prime}} \over {{\rm d}\Omega}} {\rm d}\Omega,}$$
$$\eqalign{ W &= \int {{\rm d}\vec r{\rm d}t{\rm d}\vec p{\rm d}{\vec k}_{\rm L}n_{\rm e}(\vec r,t){\kern 1pt} \,n_{\rm L}(\vec r,t)\,{\rm \phi} _{\rm e}(\vec p)\,{\rm \phi} _{\rm L}({\vec k}_{\rm L})(c - {{\rm \vec {\rm \kappa}}} _{\rm L}\vec v)} \cr & \quad \times\displaystyle{{{\rm d \sigma} ({\vec {\rm \kappa} ^{\,\prime}})} \over {{\rm d}{\Omega} ^{\prime}}}\displaystyle{{{\rm d}{\Omega} ^{\prime}} \over {{\rm d}\Omega}} {\rm d}\Omega,}$$
with using the normalized distribution functions:
Note that (A6) includes an averaging over the momentums of colliding particles unlike Eq. (A3). The energy and angular spread of the momentums, especially of electron momentums, is very important due to their strong effect on the spectral and angular properties of the output X-ray radiation. One can see also the dominant role of the electrons from formula (2) in Section 2.
Formula (A6) is the example of explicit expression for the RY W introduced in Section 2. The value of W contains full information about the structure of the colliding beams and interparticle interaction, that is, kinematics and dynamics of the explored reaction in the colliding beams. The usage of RY W proves to be very convenient for design and review purposes in a study of electron and IR photon X-ray sources and evaluation of the output X-ray flux.
In the subsection below the electron and laser photon distribution functions will be taken as Gaussian to produce a convenient form of the equations for Monte Carlo simulation of the output X-ray flux.
A1.2. Parameterization of the colliding beams
In practice the TXRG spectrum can be adequately described with a replacement of the particle densities in Eq. (A6) with the standard Gaussian functions:
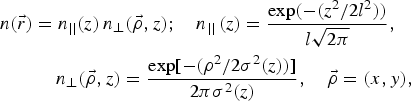 $$\eqalign{& n(\vec r) = n_{ \vert \vert} (z)\,n_ \bot ({\rm \vec {\rm \rho}}, z);\quad n_{ \vert \vert} \left( z \right) = \displaystyle{{\exp ( - (z^2/2l^2))} \over {l\sqrt {2{\rm \pi}}}}, \cr &\quad\quad\quad n_ \bot (\vec {\rm \rho}, z) = \displaystyle{{\exp [ - ({\rm \rho} ^2/2{\rm \sigma} ^2(z))]} \over {2{\rm \pi} {\rm \sigma} ^2(z)}},\quad {\rm \vec {\rm \rho}} = (x,y),}$$
$$\eqalign{& n(\vec r) = n_{ \vert \vert} (z)\,n_ \bot ({\rm \vec {\rm \rho}}, z);\quad n_{ \vert \vert} \left( z \right) = \displaystyle{{\exp ( - (z^2/2l^2))} \over {l\sqrt {2{\rm \pi}}}}, \cr &\quad\quad\quad n_ \bot (\vec {\rm \rho}, z) = \displaystyle{{\exp [ - ({\rm \rho} ^2/2{\rm \sigma} ^2(z))]} \over {2{\rm \pi} {\rm \sigma} ^2(z)}},\quad {\rm \vec {\rm \rho}} = (x,y),}$$
where for the electrons:
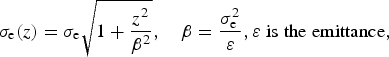 $${\rm \sigma} _{\rm e}(z) = {\rm \sigma} _{\rm e}\sqrt {1 + \displaystyle{{z^2} \over {{\rm \beta} ^2}}}, \quad {\rm \beta} = \displaystyle{{{\rm \sigma} _{\rm e}^{\rm 2}} \over {\rm \varepsilon}}, {\rm \varepsilon} \;{\rm is}\;{\rm the}\;{\rm emittance,}$$
$${\rm \sigma} _{\rm e}(z) = {\rm \sigma} _{\rm e}\sqrt {1 + \displaystyle{{z^2} \over {{\rm \beta} ^2}}}, \quad {\rm \beta} = \displaystyle{{{\rm \sigma} _{\rm e}^{\rm 2}} \over {\rm \varepsilon}}, {\rm \varepsilon} \;{\rm is}\;{\rm the}\;{\rm emittance,}$$
and for the photons:
 $$\eqalign{& {\rm \sigma} _{\rm L}(z) = {\rm \sigma} _{\rm L}\sqrt {1 + \displaystyle{{z^2} \over {z_{\rm R}^{\rm 2}}}}, \quad z_{\rm R} = \displaystyle{{4{\rm \pi} {\rm \sigma} _{\rm L}^{\rm 2}} \over {\rm \lambda}} \quad {\rm is}\;{\rm the}\;{\rm Raleigh}\;{\rm length}.}$$
$$\eqalign{& {\rm \sigma} _{\rm L}(z) = {\rm \sigma} _{\rm L}\sqrt {1 + \displaystyle{{z^2} \over {z_{\rm R}^{\rm 2}}}}, \quad z_{\rm R} = \displaystyle{{4{\rm \pi} {\rm \sigma} _{\rm L}^{\rm 2}} \over {\rm \lambda}} \quad {\rm is}\;{\rm the}\;{\rm Raleigh}\;{\rm length}.}$$
Note that according to (A8) the intervals [−σ/4, −σ/4] and [−σ/2, −σ/2] contain only 1/8 and 2/5 of the total number of particles, respectively. In electron momentum distribution function
![]() ${\rm \varphi} _{\rm e}(\vec p)$
we use the relativistic factor γ instead of p, so that:
${\rm \varphi} _{\rm e}(\vec p)$
we use the relativistic factor γ instead of p, so that:
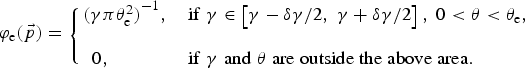 $${\rm \varphi}_{\rm e}(\vec p) = \left\{ {\matrix{ {{({\rm \gamma}{\rm \pi} {\rm \theta} _{\rm e}^{\rm 2} )}^{ - 1},\quad {\rm if}\;{\rm \gamma} \in \left[ {{\rm \gamma} - {\rm \delta} {\rm \gamma} /2,\;{\rm \gamma} + {\rm \delta} {\rm \gamma} /2} \right],\;0 \lt {\rm \theta} \lt {\rm \theta} _{\rm e},} \cr {\matrix{ {} \cr {\hskip-2pc0,\hskip3.2pc\;{\rm if}\;{\rm \gamma} \;{\rm and}\;{\rm \theta} \;{\rm are}\;{\rm outside}\;{\rm the}\;{\rm above}\;{\rm area}.} \cr } } \cr } } \right.$$
$${\rm \varphi}_{\rm e}(\vec p) = \left\{ {\matrix{ {{({\rm \gamma}{\rm \pi} {\rm \theta} _{\rm e}^{\rm 2} )}^{ - 1},\quad {\rm if}\;{\rm \gamma} \in \left[ {{\rm \gamma} - {\rm \delta} {\rm \gamma} /2,\;{\rm \gamma} + {\rm \delta} {\rm \gamma} /2} \right],\;0 \lt {\rm \theta} \lt {\rm \theta} _{\rm e},} \cr {\matrix{ {} \cr {\hskip-2pc0,\hskip3.2pc\;{\rm if}\;{\rm \gamma} \;{\rm and}\;{\rm \theta} \;{\rm are}\;{\rm outside}\;{\rm the}\;{\rm above}\;{\rm area}.} \cr } } \cr } } \right.$$
The photon distribution in
![]() $\vec k_{\rm L}$
space can be rewritten in the similar form as well.
$\vec k_{\rm L}$
space can be rewritten in the similar form as well.
Parameterization (A8)–(A11) is useful for both numerical and analytical calculations of the RY W [see (A6)]. In a number of simple or special cases, the corresponding analytical formula can be derived, that provides an effective tool for analysis of TXRG design, device scaling, accelerator and laser parameters and so on. Thus, a head-on collision of ideally synchronized beams presents an example of simple geometry of the colliding beams. In this case the electron and photon densities (A8) can be written in the form (Brown & Hartemann, Reference Brown and Hartemann2004):
APPENDIX B
B1. THE MONTE CARLO SIMULATION OF THE THOMSON SCATTERING
The Monte Carlo method is an effective numerical method for solving complex mathematical problems with the help of random variables. A simulation of the electron-photon collision processes, for example, Compton or Thomson scattering, is a typical example with a 50-years long story of successful applications in space and laboratory physics (Pozdnyakov et al., Reference Pozdnyakov, Sobol and Syunyaev1983; Sobol, Reference Sobol1994; Krivosheyev et al., Reference Krivosheyev, Bisnovatyi-Kogan, Cherepashchuk and Postnov2009). Below we will present the Monte Carlo basics (Sobol, Reference Sobol1994) as well as specific details of our computer implementation of the Thomson scattering simulation.
The trajectory of each electron in the laser–electron interaction zone is divided into intervals
![]() $[\vec v_i \cdot t_i,\,\vec v_i \cdot (t_i + \Delta t)]$
, where the laser photon density and unit vector are considered to be
$[\vec v_i \cdot t_i,\,\vec v_i \cdot (t_i + \Delta t)]$
, where the laser photon density and unit vector are considered to be
![]() $n_{\rm L}(\vec r_i,t_i)$
and
$n_{\rm L}(\vec r_i,t_i)$
and
![]() $\vec {\rm \kappa} _{{\rm L},\;i}$
, respectively (see Fig. 3). Then, the probability dP
i
of the Thomson scattering on ith segment can be written as:
$\vec {\rm \kappa} _{{\rm L},\;i}$
, respectively (see Fig. 3). Then, the probability dP
i
of the Thomson scattering on ith segment can be written as:
where σT is the total cross-section of the Thomson scattering,
![]() $\vec v_i$
is the electron velocity, and c is the light speed.
$\vec v_i$
is the electron velocity, and c is the light speed.
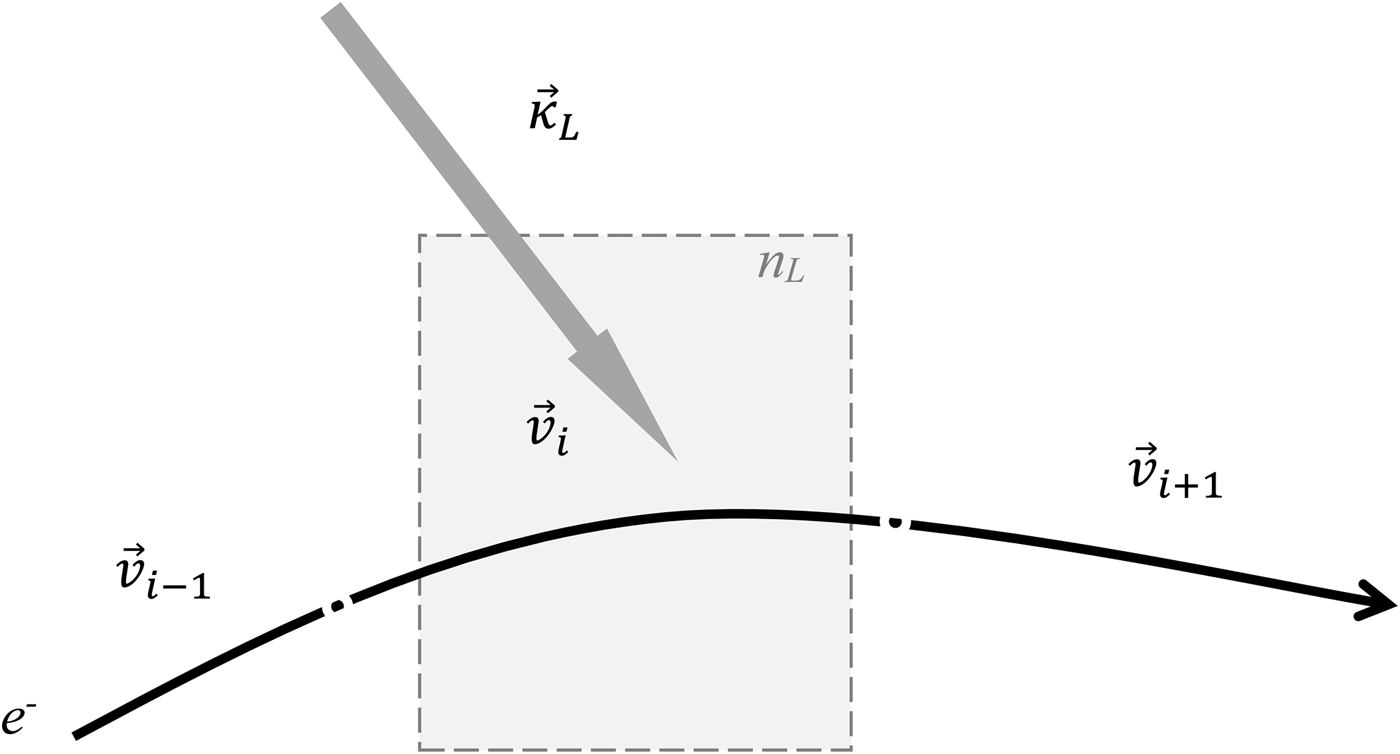
Fig. 3. Scheme of the Thomson scattering in the Monte Carlo simulation.
According to the random sampling approach, the event of electron–photon scattering will be counted only, if dP i > r 1, with r 1 being a random number distributed uniformly in the range [0, 1]. Due to low cross-sectional values and, consequently, low probability dP i of the Thomson scattering we check this condition for the given electron only once after this condition met. Then the computation of the electron trajectory stops, and we determine the properties of the scattered X-ray photon.
The “rare events collisions” is the main assumption validating the described Monte Carlo approach and formula (B1). It results from the fact that a laser photon pathlength is much longer than the electron bunch length in all known linac designs. Multiple collisions and the corresponding spectrum of relativistic Thomson and Compton scattering is studied in Potylitsyn and Kolchuzhkin (Reference Potylitsyn and Kolchuzhkin2014).
In the rest frame of the particular electron, the differential cross-section of the Thomson scattering is:
where θ′ is the scattering angle of the X-ray photon (see Fig. 3). The corresponding probability function F is:
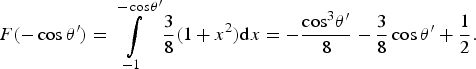 $$\eqalign{& F( - \cos {\rm \theta} {\rm ^{\prime}}) = \int\limits_{ - 1}^{ - \cos {\rm \theta} {\rm ^{\prime}}} {\displaystyle{3 \over 8}} (1 + x^2){\rm d}x = - \displaystyle{{{\cos} ^3{\rm \theta} {\rm ^{\prime}}} \over 8} - \displaystyle{3 \over 8}\cos {\rm \theta} {\rm ^{\prime}} + \displaystyle{1 \over 2}.}$$
$$\eqalign{& F( - \cos {\rm \theta} {\rm ^{\prime}}) = \int\limits_{ - 1}^{ - \cos {\rm \theta} {\rm ^{\prime}}} {\displaystyle{3 \over 8}} (1 + x^2){\rm d}x = - \displaystyle{{{\cos} ^3{\rm \theta} {\rm ^{\prime}}} \over 8} - \displaystyle{3 \over 8}\cos {\rm \theta} {\rm ^{\prime}} + \displaystyle{1 \over 2}.}$$
Then the scattering angles φ′ and θ′ of the scattered photon can be modeled as:
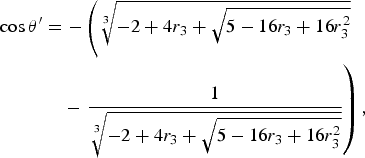 $$\eqalign{\cos {\rm \theta} {\rm ^{\prime}} & = - \left( {\root 3 \of { - 2 + 4r_3 + \sqrt {{\rm 5 - 16}r_3 + {\rm 16}r_3^{\rm 2}}}} \right. \cr & \quad - \left. {\displaystyle{1 \over {\root 3 \of { - 2 + 4r_3 + \sqrt {{\rm 5 - 16}r_3 + {\rm 16}r_3^{\rm 2}}}}}} \right),}$$
$$\eqalign{\cos {\rm \theta} {\rm ^{\prime}} & = - \left( {\root 3 \of { - 2 + 4r_3 + \sqrt {{\rm 5 - 16}r_3 + {\rm 16}r_3^{\rm 2}}}} \right. \cr & \quad - \left. {\displaystyle{1 \over {\root 3 \of { - 2 + 4r_3 + \sqrt {{\rm 5 - 16}r_3 + {\rm 16}r_3^{\rm 2}}}}}} \right),}$$
where r
2 and r
3 are uniformly distributed random numbers in the range [0, 1]. Finally, the calculated vector
![]() $\vec k^{\prime}_i$
of scattered X-ray photon is converted to the laboratory frame.
$\vec k^{\prime}_i$
of scattered X-ray photon is converted to the laboratory frame.
If the condition dP i > r 1 is failed, we have to continue the simulation of the electron trajectory and laser photon properties over all the following segments until either Thomson scattering act or leaving the interaction zone.
Our program for TXRG Monte Carlo simulation has got two options: (1) the calculations are made with a given dataset
![]() $\{ \vec r_i, \vec p_i\} $
containing needed kinetic parameters of the electron ensemble; or (2) the program generates the input dataset
$\{ \vec r_i, \vec p_i\} $
containing needed kinetic parameters of the electron ensemble; or (2) the program generates the input dataset
![]() $\{ \vec r_i, \vec p_i\} $
itself.
$\{ \vec r_i, \vec p_i\} $
itself.
In the presented review, we use the second option: the electron distribution is calculated with the help of a special subroutine:
 $$\eqalign{& (x - x_0)^2/({\rm \varepsilon} _x{\rm \beta} _x) + (y - y_0)^2/({\rm \varepsilon} _y{\rm \beta} _y) + (z - z_0)^2/l_{\rm e}^2 \le 1 \cr & (\,p_x - p_{x{\rm 0}})^2/({\rm \varepsilon} _x/{\rm \beta} _x) + (\,p_y - p_{y0})^2/({\rm \varepsilon} _y/{\rm \beta} _y) \cr & \quad + (\,p_z - p_{z{\rm 0}})^2/\Delta {\rm \gamma} ^2 \le p_{z{\rm 0}}^2 \cr & (x - x_0)^2/{\rm \beta} _x + ((\,p_x - p_{x{\rm 0}})/p_{z{\rm 0}})^2{\rm \beta} _x \le {\rm \varepsilon} _x \cr & (y - y_0)^2/{\rm \beta} _y + ((\,p_y - p_{y{\rm 0}})/p_{z{\rm 0}})^2{\rm \beta} _y \le {\rm \varepsilon} _y \cr & (z - z_0)^2\Delta {\rm \gamma} /l_{\rm e} + ({\rm \gamma} - {\rm \gamma} _0)^2l_{\rm e}/\Delta {\rm \gamma} \le l_{\rm e}\Delta {\rm \gamma},}$$
$$\eqalign{& (x - x_0)^2/({\rm \varepsilon} _x{\rm \beta} _x) + (y - y_0)^2/({\rm \varepsilon} _y{\rm \beta} _y) + (z - z_0)^2/l_{\rm e}^2 \le 1 \cr & (\,p_x - p_{x{\rm 0}})^2/({\rm \varepsilon} _x/{\rm \beta} _x) + (\,p_y - p_{y0})^2/({\rm \varepsilon} _y/{\rm \beta} _y) \cr & \quad + (\,p_z - p_{z{\rm 0}})^2/\Delta {\rm \gamma} ^2 \le p_{z{\rm 0}}^2 \cr & (x - x_0)^2/{\rm \beta} _x + ((\,p_x - p_{x{\rm 0}})/p_{z{\rm 0}})^2{\rm \beta} _x \le {\rm \varepsilon} _x \cr & (y - y_0)^2/{\rm \beta} _y + ((\,p_y - p_{y{\rm 0}})/p_{z{\rm 0}})^2{\rm \beta} _y \le {\rm \varepsilon} _y \cr & (z - z_0)^2\Delta {\rm \gamma} /l_{\rm e} + ({\rm \gamma} - {\rm \gamma} _0)^2l_{\rm e}/\Delta {\rm \gamma} \le l_{\rm e}\Delta {\rm \gamma},}$$
where {x 0, y 0, z 0, p x0, p y0, p z0} is the center of the electron distribution, β x = β y = β is the beta function, ε x = ε y = ε is the electron emittance, l e is semi-length of the bunch, γ is the relativistic factor of the bunch, Δγ is a half width of the γ spectra.
The Monte Carlo program is implemented with using C++, C#, and LUA languages. For a user's convenience the program can be controlled through a www on-line interface: http://93.81.242.254:55000/fiber_web/lexg.aspx. The on-line form opens all input fields for the electron and laser beams parameters: bunch and laser pulse lengths, radii, energy, emittance, and so on. The results of the Monte Carlo? calculation for the specified TXRG parameters are to be sent to an indicated e-mail address.





