Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T21:19:17.223Z Has data issue: false hasContentIssue false
  • English
  • Français

An algorithm for NTRU problems and cryptanalysis of the GGH multilinear map without a low-level encoding of zero

Part of: Algorithms - Computer Science Computational number theory Theory of computing

Published online by Cambridge University Press:  26 August 2016

Jung Hee Cheon ,
Jinhyuck Jeong  and
Changmin Lee
Jung Hee Cheon
Affiliation:
Seoul National University, 1 Gwanak-ro, Gwanak-gu, Seoul 151-742, Republic of Korea email jhcheon@snu.ac.kr
Jinhyuck Jeong
Affiliation:
Seoul National University, 1 Gwanak-ro, Gwanak-gu, Seoul 151-42, Republic of Korea email wlsyrlekd@snu.ac.kr
Changmin Lee
Affiliation:
Seoul National University, 1 Gwanak-ro, Gwanak-gu, Seoul 151-742, Republic of Korea email cocomi11@snu.ac.kr

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 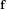$\mathbf{f}$ and $\mathbf{g}$ be polynomials of a bounded Euclidean norm in the ring 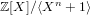$\mathbb{Z}[X]/\langle X^{n}+1\rangle$. Given the polynomial 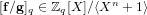$[\mathbf{f}/\mathbf{g}]_{q}\in \mathbb{Z}_{q}[X]/\langle X^{n}+1\rangle$, the NTRU problem is to find $\mathbf{a},\mathbf{b}\in \mathbb{Z}[X]/\langle X^{n}+1\rangle$ with a small Euclidean norm such that 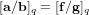$[\mathbf{a}/\mathbf{b}]_{q}=[\mathbf{f}/\mathbf{g}]_{q}$. We propose an algorithm to solve the NTRU problem, which runs in 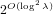$2^{O(\log ^{2}\unicode[STIX]{x1D706})}$ time when 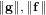$\Vert \mathbf{g}\Vert ,\Vert \mathbf{f}\Vert$, and 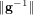$\Vert \mathbf{g}^{-1}\Vert$ are within some range. The main technique of our algorithm is the reduction of a problem on a field to one on a subfield. The GGH scheme, the first candidate of an (approximate) multilinear map, was recently found to be insecure by the Hu–Jia attack using low-level encodings of zero, but no polynomial-time attack was known without them. In the GGH scheme without low-level encodings of zero, our algorithm can be directly applied to attack this scheme if we have some top-level encodings of zero and a known pair of plaintext and ciphertext. Using our algorithm, we can construct a level-$0$ encoding of zero and utilize it to attack a security ground of this scheme in the quasi-polynomial time of its security parameter using the parameters suggested by Garg, Gentry and Halevi [‘Candidate multilinear maps from ideal lattices’, Advances in cryptology — EUROCRYPT 2013 (Springer, 2013) 1–17].

MSC classification

Primary: 11Y16: Algorithms; complexity
Secondary: 68Q25: Analysis of algorithms and problem complexity 68W40: Analysis of algorithms
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 255 - 266
Copyright
© The Author(s) 2016 

References

Aggarwal, D., Dadush, D., Regev, O. and Stephens-Davidowitz, N., ‘Solving the shortest vector problem in $2^{n}$ time via discrete Gaussian sampling’, Preprint, 2014, arXiv:1412.7994.CrossRefGoogle Scholar
Albrecht, M. R., Bai, S. and Ducas, L., ‘A subfield lattice attack on overstretched NTRU assumptions: cryptanalysis of some FHE and graded encoding schemes’, Advances in cryptology — CRYPTO 2016 (Springer, Berlin, 2016) 153–178.Google Scholar
Albrecht, M. R., Cocis, C., Laguillaumie, F. and Langlois, A., ‘Implementing candidate graded encoding schemes from ideal lattices’, Advances in cryptology — ASIACRYPT 2015 (Springer, Berlin, 2015) 752–775.Google Scholar
Boneh, D. and Silverberg, A., ‘Applications of multilinear forms to cryptography’, Topics in algebraic and noncommutative geometry , Contemporary Mathematics 324 (eds Melles, C. G., Brasselet, J.-P., Kennedy, G., Lauter, K. and McEwan, L.; American Mathematical Society, Providence, RI, 2003) 71–90.Google Scholar
Bos, J. W., Lauter, K., Loftus, J. and Naehrig, M., ‘Improved security for a ring-based fully homomorphic encryption scheme’, Cryptography and coding 2013 (Springer, Berlin, 2013) 45–64.Google Scholar
Cheon, J. H., Han, K., Lee, C., Ryu, H. and Stehlé, D., ‘Cryptanalysis of the multilinear map over the integers’, Advances in cryptology — EUROCRYPT 2015 (Springer, Berlin, 2015) 3–12.Google Scholar
Cheon, J. H., Lee, C. and Ryu, H., ‘Cryptanalysis of the new CLT multilinear maps’, Advances in cryptology — EUROCRYPT 2016 (Springer, Berlin, 2016) 509–536.CrossRefGoogle Scholar
Coron, J.-S., ‘Cryptanalysis of GGH15 multilinear maps’, Advances in cryptology — CRYPTO 2016 (Springer, Berlin, 2016) 607–628.CrossRefGoogle Scholar
Coron, J.-S., Lepoint, T. and Tibouchi, M., ‘Practical multilinear maps over the integers’, Advances in cryptology — CRYPTO 2013 (Springer, Berlin, 2013) 476–493.Google Scholar
Coron, J.-S., Lepoint, T. and Tibouchi, M., ‘New multilinear maps over the integers’, Advances in cryptology — CRYPTO 2015 (Springer, Berlin, 2015) 267–286.Google Scholar
Ducas, L., Durmus, A., Lepoint, T. and Lyubashevsky, V., ‘Lattice signatures and bimodal Gaussians’, Advances in cryptology – CRYPTO 2013 (Springer, Berlin, 2013) 40–56.Google Scholar
Garg, S., Gentry, C. and Halevi, S., ‘Candidate multilinear maps from ideal lattices’, Advances in cryptology – EUROCRYPT 2013 (Springer, Berlin, 2013) 1–17.Google Scholar
Garg, S., Gentry, C. and Halevi, S., ‘Graph-induced multilinear maps from lattices’, Theory of cryptography 2015 (Springer, Berlin, 2015) 498–527.Google Scholar
Gentry, C. and Szydlo, M., ‘Cryptanalysis of the revised NTRU signature scheme’, Advances in cryptology — EUROCRYPT 2002 (Springer, Berlin, 2002).Google Scholar
Hanrot, G., Pujol, X. and Stehlé, D., ‘Terminating BKZ’, IACR Cryptology ePrint Archive 2011, https://eprint.iacr.org/2011/198.Google Scholar
Hoffstein, J., Howgrave-Graham, N., Pipher, J., Silverman, J. H. and Whyte, W., ‘NTRUSIGN: digital signatures using the NTRU lattice’, Topics in cryptology — CT-RSA 2003 (Springer, Berlin, 2003) 122–140.Google Scholar
Hoffstein, J., Pipher, J. and Silverman, J. H., ‘NTRU: a ring-based public key cryptosystem’, Algorithmic number theory 1998 (Springer, Berlin, 1998) 267–288.CrossRefGoogle Scholar
Hu, Y. and Jia, H., ‘Cryptanalysis of GGH map’, Advances in cryptology — EUROCRYPT 2016 (Springer, Berlin, 2016) 537–565.Google Scholar
Langlois, A., Stehlé, D. and Steinfeld, R., ‘GGHLite: more efficient multilinear maps from ideal lattices’, Advances in cryptology — EUROCRYPT 2014 (Springer, Berlin, 2014) 239–256.Google Scholar
López-Alt, A., Tromer, E. and Vaikuntanathan, V., ‘On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption’, Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing 2012 (ACM, New York, NY, 2012) 1219–1234.Google Scholar
Miles, E., Sahai, A. and Zhandry, M., ‘Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13’, Advances in cryptology — CRYPTO 2016 (Springer, Berlin, 2016) 491–520.Google Scholar