Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T05:03:29.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation by a composition of Chlodowsky operators and Százs–Durrmeyer operators on weighted spaces

Part of: Approximations and expansions

Published online by Cambridge University Press:  01 October 2013

Aydın İzgi
Aydın İzgi*
Affiliation:
Matematik Bölümü,Harran Üniversitesi,Fen-Edebiyat Fakültesi,Osmanbey Kampüsü,63300 Sanliurfa,Turkey email aydinizgi@yahoo.com, aydinizgi1@gmail.com

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we deal with the operators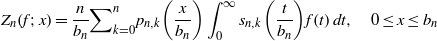

$$\begin{eqnarray*}{Z}_{n} (f; x)= \frac{n}{{b}_{n} } { \mathop{\sum }\nolimits}_{k= 0}^{n} {p}_{n, k} \biggl(\frac{x}{{b}_{n} } \biggr)\int \nolimits \nolimits_{0}^{\infty } {s}_{n, k} \biggl(\frac{t}{{b}_{n} } \biggr)f(t)\hspace{0.167em} dt, \quad 0\leq x\leq {b}_{n}\end{eqnarray*}$$
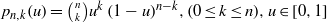and study some basic properties of these operators where ${p}_{n, k} (u)=\bigl(\hspace{-4pt}{\scriptsize \begin{array}{ l} \displaystyle n\\ \displaystyle k\end{array} } \hspace{-4pt}\bigr){u}^{k} \mathop{(1- u)}\nolimits ^{n- k} , (0\leq k\leq n), u\in [0, 1] $ and 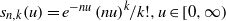${s}_{n, k} (u)= {e}^{- nu} \mathop{(nu)}\nolimits ^{k} \hspace{-3pt}/ k!, u\in [0, \infty )$. Also, we establish the order of approximation by using weighted modulus of continuity.

MSC classification

Secondary: 41A10: Approximation by polynomials 41A25: Rate of convergence, degree of approximation 41A30: Approximation by other special function classes 41A36: Approximation by positive operators
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 16 , October 2013 , pp. 388 - 397
Copyright
© The Author(s) 2013 

References

Achieser, N. I., Lectures on the theory of approximation (OGIZ, Moscow–Leningrad, 1947) (Russian); Theory of approximation, translated by C. J. Hymann (Frederick Ungar, New York, 1956) 208–226.Google Scholar
Becker, M., ‘Global approximation theorems for Szász–Mirakjan and Baskakov operators in polynomial weight spaces’, Indiana Univ. Math. J. (1978) 127–142.CrossRefGoogle Scholar
Chlodowsky, I., ‘Sur le développment des fonctions défines dans un interval infinien séries de polynómes de S. N. Bernstein’, Compositio Math. 4 (1937) 380–392.Google Scholar
Coşkun, T., ‘Some properties of linear positive operators on the spaces of weight functions’, Commun. Fac. Sci. Univ. Ank. Sér. A1 47 (1998) 175–181.Google Scholar
Coşkun, T., ‘Weighted approximation of continuous functions by sequences of linear positive operators’, Proc. Indian Acad. Sci. (Math. Sci.) 110 (2000) 357–362.CrossRefGoogle Scholar
Ditzian, Z., ‘Convergence of sequences of linear positive operators: remarks and applications’, J. Approx. Theory 14 (1975) 296–301.CrossRefGoogle Scholar
Ditzian, Z., ‘On global invers theorems of Szăsz and Baskakov operators’, Canad. J. Math. 31 (1972) 255–263.CrossRefGoogle Scholar
Doğru, O., ‘Weighted approximation of continuous functions on the all positive axis by modified linear positive operators’, Int. J. Comput. Numer. Anal. Appl. 1 (2002) 135–147.Google Scholar
Durrmeyer, J. L., ‘Une formule d’inversion de la transformee de Laplace: Applications a la theorie de moments’, these de 3e cycle, Faculte des sciences de 1’universite de Paris (1967).Google Scholar
Gadzhiev, A. D., ‘The convergence problem for a sequence of linear operators on unbounded sets and theorem analogous to that of P. P. Korovkin’, Soviet Math. Dokl. 15 (1974) 1433–1436.Google Scholar
Gadzhiev, A. D., ‘Theorems of the type P. P. Korovkin theorems’, Math. Zametki 20 (1976) 781–786; English translation in Math. Notes 20 (1976), 996–998.Google Scholar
Gadzhiev, A. D., Efendiev, R. O. and Ibikli, E., ‘Generalized Bernstein–Chlodowsky polynomials’, Rocky Mount. J. Math. 28 (1998) 1267–1277.Google Scholar
Gadzhieva, E. A. and Ibikli, E., ‘Weighted approximation by Bernstein–Chlodowsky polynomials’, Indian J. Pure Appl. Math. 30 (1999) 83–87.Google Scholar
Gupta, V., ‘Simultaneous approximation by Szăsz–Durrmeyer operators’, Math. Student 64 (1995) 27–36.Google Scholar
Gupta, V. and Agarval, P. N., ‘An estimation of the rate of convergence for modified Szăsz–Mirakjan operators of functions of bounded variation’, Publ. Inst. Math. (Beograd) (N.S.) 49 (1991) 97–103.Google Scholar
Ibikli, E., ‘On approximation by Bernstein–Chlodowsky polynomials’, Math. Balkanica (N.S.) 17 (2003) 259–265.Google Scholar
Ibikli, E. and Karslı, H., ‘Rate of convergence of Chlodowsky type Durrmeyer operators’, J. Inequal. Pure Appl. Math. 6 (2005) no. 4, paper 106.Google Scholar
Ibikli, E., Izgi, A. and Buyukyazıcı, I., Approximation of ${L}^{p} $ - integrable functions by linear positive operators. ICCAM 2006, 10–14 July.Google Scholar
Ispir, N., ‘On modified Baskakov operators on weighted spaces’, Turkish J. Math. 26 (2001) 355–365.Google Scholar
Ispir, N. and Atakut, Ç., ‘Approximation by modified Szasz–Mirakjan operators on weighted spaces’, Proc. Indian Acad. Sci. (Math. Sci.) 112 (2002) 571–578.CrossRefGoogle Scholar
Lešniewicz, M. and Rempluska, L. R., ‘Approximation by some operators of Szasz–Mirakjan type in exponential weight spaces’, Glas. Mat. 32 (1997) 57–69.Google Scholar
May, C. P., ‘Saturation and inverse theorems for combinations of class of exponential type operators’, Canad. J. Math. 28 (1976) 1224–1250.CrossRefGoogle Scholar
Mazhar, S. M. and Totik, V., ‘Approximation by modified Szász operators’, Acta Sci. Math. 49 (1985) 257–269.Google Scholar
Walczak, Z., ‘On certain linear positive operators in exponential weighted spaces’, Math. J. Tojama Univ. 25 (2002) 19–118.Google Scholar