Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T05:04:49.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Character theory approach to Sato–Tate groups

Part of: Arithmetic algebraic geometry Representation theory of groups Zeta and $L$-functions: analytic theory Arithmetic problems. Diophantine geometry Abelian varieties and schemes

Published online by Cambridge University Press:  26 August 2016

Yih-Dar Shieh
Yih-Dar Shieh*
Affiliation:
Institut de Mathématiques de Marseille, 163, avenue de Luminy, Case 907, 13288 Marseille Cedex 9, France email chiapas@gmail.com http://yih-dar.shieh.perso.luminy.univ-amu.fr/

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article, we propose to use the character theory of compact Lie groups and their orthogonality relations for the study of Frobenius distribution and Sato–Tate groups. The results show the advantages of this new approach in several aspects. With samples of Frobenius ranging in size much smaller than the moment statistic approach, we obtain very good approximation to the expected values of these orthogonality relations, which give useful information about the underlying Sato–Tate groups and strong evidence of the correctness of the generalized Sato–Tate conjecture. In fact, 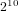$2^{10}$ to $2^{12}$ points provide satisfactory convergence. Even for 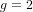$g=2$, the classical approach using moment statistics requires about 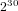$2^{30}$ sample points to obtain such information.

MSC classification

Primary: 11M50: Relations with random matrices
Secondary: 20C15: Ordinary representations and characters 11G10: Abelian varieties of dimension $> 1$ 11G20: Curves over finite and local fields 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture) 14K15: Arithmetic ground fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 301 - 314
Copyright
© The Author 2016 

References

Bump, D., Lie groups , 2nd edn (Springer, New York, 2013), doi:10.1007/978-1-4614-8024-2.Google Scholar
Bump, D., Salisbury, B. and Schilling, A., Lie methods and related combinatorics in Sage. URL: http://doc.sagemath.org/html/en/thematic_tutorials/lie/weyl_character_ring.html.Google Scholar
Fité, F., Kedlaya, K., Rotger, V. and Sutherland, A., ‘Sato–Tate distributions and Galois endomorphism modules in genus 2’, Compositio. Math. 148 (2012) no. 5, 1390–1442, doi:10.1112/S0010437X12000279.CrossRefGoogle Scholar
Fité, F. and Sutherland, A., ‘Sato–Tate groups of $y^{2}=x^{8}+c$ and $y^{2}=x^{7}-cx$ ’, Preprint, 2014, arXiv:1412.0125v2.Google Scholar
Harvey, D., ‘Counting points on hyperelliptic curves in average polynomial time’, Ann. of Math. (2) 179 (2014) no. 2, 783–803, doi:10.4007/annals.2014.179.2.7.CrossRefGoogle Scholar
Harvey, D. and Sutherland, A. V., ‘Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time’, LMS J. Comput. Math. 17A (2014) 257–273, doi:10.1112/S1461157014000187.Google Scholar
Harvey, D. and Sutherland, A. V., ‘Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time, II’, Frobenius distributions: Lang–Trotter and Sato–Tate conjectures , Contemporary Mathematics 663 (eds Kohel, D. and Shparlinski, I.; American Mathematical Society, Providence, RI, 2016) 127–148.CrossRefGoogle Scholar
Iwasawa, K., ‘On 𝛤-extensions of algebraic number fields’, Bull. Amer. Math. Soc. (N.S.) 65 (1959) no. 4, 183–226. URL: http://projecteuclid.org/euclid.bams/1183523193.Google Scholar
Kedlaya, K. S., ‘Sato–Tate groups of genus 2 curves’, Preprint, 2014, arXiv:1408.6968 [math.NT].Google Scholar
Kedlaya, K. S. and Sutherland, A. V., ‘Computing L-series of hyperelliptic curves’, Algorithmic number theory , Proceedings of 8th International Symposium, ANTS-VIII Banff, Canada, May 17–22, 2008 (Springer, Berlin, 2008) 312–326, doi:10.1007/978-3-540-79456-1_21.CrossRefGoogle Scholar
Serre, J.-P., Lectures on N X (p) (CRC Press, Boca Raton, FL, 2012).Google Scholar
Serre, J.-P. and Tate, J., ‘Good reduction of abelian varieties’, Ann. of Math. (2) 88 (1968) 492–517, doi:10.2307/1970722.Google Scholar
Shieh, Y.-D., ‘Arithmetic aspects of point counting and Frobenius distributions’, PhD Thesis, Institut de Mathématiques de Marseille, 2015,http://yih-dar.shieh.perso.luminy.univ-amu.fr/publications/Thesis-SHIEH.pdf.Google Scholar
Sutherland, A. V., ‘smalljac software library, version 4.0, 2011’, http://math.mit.edu/∼drew.Google Scholar
Sutherland, A. V., ‘Sato–Tate distributions’, Preprint, 2016, arXiv:1604.01256 [math.NT].Google Scholar
Sutherland, A. V., ‘Order computations in generic groups’, PhD Thesis, MIT, 2007.Google Scholar
Washington, L. C., Introduction to cyclotomic fields , 2nd edn (Springer, New York, 1997).CrossRefGoogle Scholar