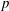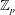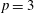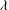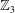Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Murakami, Kazuaki
2023.
A weak form of Greenberg's generalized conjecture for imaginary quadratic fields.
Journal of Number Theory,
Vol. 244,
Issue. ,
p.
308.