Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T22:45:21.891Z Has data issue: false hasContentIssue false
  • English
  • Français

Complexity of OM factorizations of polynomials over local fields

Part of: Computational number theory Topological fields Curves

Published online by Cambridge University Press:  01 June 2013

Jens-Dietrich Bauch ,
Enric Nart  and
Hayden D. Stainsby
Jens-Dietrich Bauch
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, Edifici C, E-08193 Bellaterra, Barcelona, Catalonia, Spain email bauch@mat.uab.catnart@mat.uab.cathds@mat.uab.cat
Enric Nart
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, Edifici C, E-08193 Bellaterra, Barcelona, Catalonia, Spain email bauch@mat.uab.catnart@mat.uab.cathds@mat.uab.cat
Hayden D. Stainsby
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, Edifici C, E-08193 Bellaterra, Barcelona, Catalonia, Spain email bauch@mat.uab.catnart@mat.uab.cathds@mat.uab.cat

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

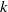Let $k$ be a locally compact complete field with respect to a discrete valuation $v$. Let 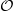$ \mathcal{O} $ be the valuation ring, 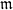$\mathfrak{m}$ the maximal ideal and 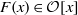$F(x)\in \mathcal{O} [x] $ a monic separable polynomial of degree $n$. Let 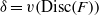$\delta = v(\mathrm{Disc} (F))$. The Montes algorithm computes an OM factorization of 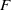$F$. The single-factor lifting algorithm derives from this data a factorization of 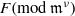$F(\mathrm{mod~} {\mathfrak{m}}^{\nu } )$, for a prescribed precision $\nu $. In this paper we find a new estimate for the complexity of the Montes algorithm, leading to an estimation of 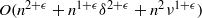$O({n}^{2+ \epsilon } + {n}^{1+ \epsilon } {\delta }^{2+ \epsilon } + {n}^{2} {\nu }^{1+ \epsilon } )$ word operations for the complexity of the computation of a factorization of 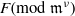$F(\mathrm{mod~} {\mathfrak{m}}^{\nu } )$, assuming that the residue field of 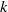$k$ is small.

MSC classification

Secondary: 11Y40: Algebraic number theory computations 11Y05: Factorization 12J10: Valued fields 14H25: Arithmetic ground fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 16 , October 2013 , pp. 139 - 171
Copyright
© The Author(s) 2013 

References

Ford, D., Pauli, S. and Roblot, X.-F., ‘A fast algorithm for polynomial factorization over ${ \mathbb{Q} }_{p} $ ’, J. Théor. Nombres de Bordeaux 14 (2002) 151–169.CrossRefGoogle Scholar
Ford, D. and Veres, O., ‘On the complexity of the Montes ideal factorization algorithm’, Algorithmic number theory, 9th International Symposium, ANTS-IX, Nancy, France, July 19–23, 2010, Lecture Notes in Computer Science (eds Hanrot, G., Morain, F. and Thomé, E.; Springer, 2010).Google Scholar
von zur Gathen, J. and Gerhard, J., Modern computer algebra, 2nd edn (Cambridge University Press, Cambridge, 2003).Google Scholar
Guàrdia, J., Montes, J. and Nart, E., ‘Okutsu invariants and Newton polygons’, Acta Arith. 145 (2010) 83–108.CrossRefGoogle Scholar
Guàrdia, J., Montes, J. and Nart, E., ‘Higher Newton polygons in the computation of discriminants and prime ideal decomposition in number fields’, J. Théor. Nombres Bordeaux 23 (2011) no. 3, 667–696.CrossRefGoogle Scholar
Guàrdia, J., Montes, J. and Nart, E., ‘Newton polygons of higher order in algebraic number theory’, Trans. Amer. Math. Soc. 364 (2012) no. 1, 361–416.CrossRefGoogle Scholar
Guàrdia, J., Montes, J. and Nart, E., ‘A new computational approach to ideal theory in number fields’, Found. Comput. Math. , doi:10.1007/s10208-012-9137-5.CrossRefGoogle Scholar
Guàrdia, J., Montes, J. and Nart, E., ‘Higher Newton polygons and integral bases’, arXiv:0902.3428v2 [math.NT].Google Scholar
Guàrdia, J., Nart, E. and Pauli, S., ‘Single-factor lifting and factorization of polynomials over local fields’, J. Symbolic Comput. 47 (2012) 1318–1346.CrossRefGoogle Scholar
MacLane, S., ‘A construction for absolute values in polynomial rings’, Trans. Amer. Math. Soc. 40 (1936) 363–395.CrossRefGoogle Scholar
MacLane, S., ‘A construction for prime ideals as absolute values of an algebraic field’, Duke Math. J. 2 (1936) 492–510.Google Scholar
Nart, E., ‘Okutsu–Montes representations of prime ideals of one-dimensional integral closures’, Publ. Mat. 55 (2011) no. 3, 261–294.CrossRefGoogle Scholar
Nart, E., ‘Local computation of differents and discriminants’, Math. Comput., to appear, arXiv:1205.1340v1 [math.NT].Google Scholar
Okutsu, K., ‘Construction of integral basis, I, II’, Proceedings of the Japan Academy 58, Ser. A (1982) 47–49, 87–89.Google Scholar
Ore, Ø., ‘Zur Theorie der algebraischen Körper’, Acta. Math. 44 (1923) 219–314.CrossRefGoogle Scholar
Ore, Ø., ‘Newtonsche Polygone in der Theorie der algebraischen Körper’, Math. Ann. 99 (1928) 84–117.CrossRefGoogle Scholar
Pauli, S., ‘Factoring polynomials over local fields’, J. Symbolic Comput. 32 (2001) 533–547.CrossRefGoogle Scholar
Pauli, S., ‘Factoring polynomials over local fields, II’, Algorithmic number theory, 9th International Symposium, ANTS-IX, Nancy, France, July 19–23, 2010, Lecture Notes in Computer Science (eds Hanrot, G., Morain, F. and Thomé, E.; Springer, 2010).Google Scholar
Schönhage, A. and Strassen, V., ‘Schnelle Multiplikation großer Zahlen’, Computing 7 (1971) 281–292.CrossRefGoogle Scholar