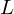Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T15:43:59.304Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing $L$-series of geometrically hyperelliptic curves of genus three

Part of: Computational number theory Arithmetic problems. Diophantine geometry Zeta and $L$-functions: analytic theory Arithmetic algebraic geometry

Published online by Cambridge University Press:  26 August 2016

David Harvey ,
Maike Massierer  and
Andrew V. Sutherland
David Harvey
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney NSW 2052, Australia email d.harvey@unsw.edu.au
Maike Massierer
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney NSW 2052, Australia email maike@unsw.edu.au
Andrew V. Sutherland
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge MA 02139, USA email drew@math.mit.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 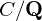$C/\mathbf{Q}$ be a curve of genus three, given as a double cover of a plane conic. Such a curve is hyperelliptic over the algebraic closure of 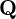$\mathbf{Q}$, but may not have a hyperelliptic model of the usual form over 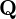$\mathbf{Q}$. We describe an algorithm that computes the local zeta functions of 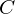$C$ at all odd primes of good reduction up to a prescribed bound 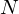$N$. The algorithm relies on an adaptation of the ‘accumulating remainder tree’ to matrices with entries in a quadratic field. We report on an implementation and compare its performance to previous algorithms for the ordinary hyperelliptic case.

MSC classification

Primary: 11G20: Curves over finite and local fields
Secondary: 11Y16: Algorithms; complexity 11M38: Zeta and $L$-functions in characteristic $p$ 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture)
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 220 - 234
Copyright
© The Author(s) 2016 

References

Booker, A. R., Sijsling, J., Sutherland, A. V., Voight, J. and Yasaki, D., ‘A database of genus-2 curves over the rational numbers’, Algorithmic Number Theory 12th International Symposium (ANTS XII), LMS J. Comput. Math., 19 (2016) special issue A, 235–254.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24 (1997) no. 3–4, 235–265; Computational algebra and number theory (London, 1993); MR 1484478.Google Scholar
Bostan, A., Gaudry, P. and Schost, É., ‘Linear recurrences with polynomial coefficients and application to integer factorization and Cartier–Manin operator’, SIAM J. Comput. 36 (2007) no. 6, 1777–1806; MR 2299425 (2008a:11156).Google Scholar
Clozel, L., Harris, M. and Taylor, R., ‘Automorphy for some l-adic lifts of automorphic mod l Galois representations’, Publ. Math. Inst. Hautes Études Sci. (2008) no. 108, 1–181; With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras; MR 2470687.Google Scholar
Cohen, H., Frey, G., Avanzi, R., Doche, C., Lange, T., Nguyen, K. and Vercauteren, F. (eds), ‘Handbook of elliptic and hyperelliptic curve cryptography’, Discrete Mathematics and its Applications (Chapman & Hall/CRC, Boca Raton, FL, 2006); MR 2162716.Google Scholar
The LMFDB Collaboration, ‘The L-functions and modular forms database’, website http://www.lmfdb.org.Google Scholar
Costa, E., Gerbicz, R. and Harvey, D., ‘A search for Wilson primes’, Math. Comp. 83 (2014) no. 290, 3071–3091; MR 3246824.Google Scholar
Cremona, J. E. and Rusin, D., ‘Efficient solution of rational conics’, Math. Comp. 72 (2003) no. 243, 1417–1441; (electronic); MR 1972744.Google Scholar
Fité, F., Kedlaya, K. S., Rotger, V. and Sutherland, A. V., ‘Sato–Tate distributions and Galois endomorphism modules in genus 2’, Compositio Math. 148 (2012) no. 5, 1390–1442; MR 2982436.Google Scholar
Fité, F. and Sutherland, A. V., ‘Sato–Tate groups of y 2 = x 8 + c and y 2 = x 7 - cx ’, Frobenius distributions: Lang–Trotter and Sato–Tate conjectures , Contemporary Mathematics 663 (American Mathematical Society, Providence, RI, 2016) 103–126.Google Scholar
Free Software Foundation, ‘GNU compiler collection, version 4.8.4’, 2013, available at http://gcc.gnu.org/.Google Scholar
Fürer, M., ‘Faster integer multiplication’, SIAM J. Comput. 39 (2009) no. 3, 979–1005.Google Scholar
Galbraith, S. D., Harrison, M. and Mireles Morales, D. J., ‘Efficient hyperelliptic arithmetic using balanced representation for divisors’, Algorithmic Number Theory 8th International Symposium (ANTS VIII) , Lecture Notes in Computational Science 5011 (Springer, Berlin, 2008) 342–356; MR 2467851.Google Scholar
González, J., ‘The Frobenius traces distribution for modular Abelian surfaces’, Ramanujan J. 33 (2014) no. 2, 247–261; MR 3165538.Google Scholar
Granlund, T. and the GMP development team, ‘GNU Multiple Precision Arithmetic Library, version 6.0’, 2015, available at http://gmplib.org/.Google Scholar
Harris, M., Shepherd-Barron, N. and Taylor, R., ‘A family of Calabi–Yau varieties and potential automorphy’, Ann. of Math. (2) 171 (2010) no. 2, 779–813; MR 2630056.Google Scholar
Harrison, M. C., ‘An extension of Kedlaya’s algorithm for hyperelliptic curves’, J. Symbolic Comput. 47 (2012) no. 1, 89–101; MR 2854849.Google Scholar
Harvey, D., ‘Kedlaya’s algorithm in larger characteristic’, Int. Math. Res. Not. IMRN (2007) no. 22, Art. ID rnm095, 29; MR 2376210 (2009d:11096).Google Scholar
Harvey, D., ‘Counting points on hyperelliptic curves in average polynomial time’, Ann. of Math. (2) 179 (2014) no. 2, 783–803; MR 3152945.Google Scholar
Harvey, D., ‘Computing zeta functions of arithmetic schemes’, Proc. Lond. Math. Soc. (3) 111 (2015) no. 6, 1379–1401; MR 3447797.Google Scholar
Harvey, D., Lecerf, G. and van der Hoeven, J., ‘Even faster integer multiplication’, J. Complexity 36 (2016) 1–30, doi:10.1016/j.jco.2016.03.001.Google Scholar
Harvey, D. and Sutherland, A. V., ‘Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time’, Algorithmic Number Theory Eleventh International Symposium (ANTS XI), Vol. 17 , London Mathematical Society Journal of Computation and Mathematics (2014) 257–273; MR 3240808.Google Scholar
Harvey, D. and Sutherland, A. V., ‘Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time, II’, Frobenius distributions: Lang–Trotter and Sato–Tate conjectures , Contemporary Mathematics 663 (American Mathematical Society, Providence, RI, 2016) 127–148.Google Scholar
Johansson, C., ‘On the Sato–Tate conjecture for non-generic abelian surfaces, with an appendix by Francesc Fité’, Trans. Amer. Math. Soc. (2016) to appear, doi:10.1090/tran/6847.Google Scholar
Katz, N. M. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy , American Mathematical Society Colloquium Publications 45 (American Mathematical Society, Providence, RI, 1999); MR 1659828.Google Scholar
Kedlaya, K. S. and Sutherland, A. V., ‘Computing L-series of hyperelliptic curves’, Algorithmic Number Theory 8th International Symposium (ANTS VIII) , Lecture Notes in Computational Science 5011 (Springer, Berlin, 2008) 312–326; MR 2467855.Google Scholar
Kedlaya, K. S. and Sutherland, A. V., ‘Hyperelliptic curves, L-polynomials, and random matrices’, Arithmetic, geometry, cryptography and coding theory , Contemporary Mathematics 487 (American Mathematical Society, Providence, RI, 2009) 119–162; MR 2555991 (2011d:11154).Google Scholar
Lario, J.-C. and Somoza, A., ‘The Sato–Tate conjecture for a Picard curve with complex multiplication’, Preprint, 2014, arXiv:1409.6020.Google Scholar
Lauder, A. G. B. and Wan, D., ‘Counting points on varieties over finite fields of small characteristic’, Algorithmic number theory: lattices, number fields, curves and cryptography , Mathematical Sciences Research Institute Publications 44 (Cambridge University Press, Cambridge, 2008) 579–612; MR 2467558 (2009j:14029).Google Scholar
Lenstra, H. W. Jr and Pomerance, C., ‘A rigorous time bound for factoring integers’, J. Amer. Math. Soc. 5 (1992) no. 3, 483–516; MR 1137100.CrossRefGoogle Scholar
Lorenzini, D., An invitation to arithmetic geometry , Graduate Studies in Mathematics 9 (American Mathematical Society, Providence, RI, 1996); MR 1376367 (97e:14035).Google Scholar
Morales, D. J. M., ‘Efficient arithmetic on hyperelliptic curves with real representation’, PhD Thesis, Royal Holloway and Bedford New College, University of London, 2008, available at https://www.math.auckland.ac.nz/∼sgal018/Dave-Mireles-Full.pdf.Google Scholar
Schönhage, A. and Strassen, V., ‘Schnelle Multiplikation grosser Zahlen’, Computing (Arch. Elektron. Rechnen) 7 (1971) 281–292; MR 0292344 (45 #1431).Google Scholar
Stein, W. A. et al. , ‘Sage Mathematics Software (Version 6.8)’, The Sage Development Team, 2015, http://www.sagemath.org.Google Scholar
Stoll, M. and Cremona, J. E., ‘On the reduction theory of binary forms’, J. reine angew. Math. 565 (2003) 79–99; MR 2024647.Google Scholar
Sutherland, A. V., ‘Order computations in generic groups’, PhD Thesis, Massachusetts Institute of Technology, 2007, available at http://groups.csail.mit.edu/cis/theses/sutherland-phd.pdf, MR 2717420.Google Scholar
Sutherland, A. V., ‘A generic approach to searching for Jacobians’, Math. Comp. 78 (2009) no. 265, 485–507; MR 2448717.CrossRefGoogle Scholar
Sutherland, A. V., ‘Fast Jacobian arithmetic for hyperelliptic curves of genus 3’, Preprint, 2016,arXiv:1607.08602.Google Scholar
Taylor, R., ‘Automorphy for some l-adic lifts of automorphic mod l Galois representations. II’, Publ. Math. Inst. Hautes Études Sci. (2008) no. 108, 183–239; MR 2470688.Google Scholar