Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T06:25:39.894Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructing supersingular elliptic curves with a given endomorphism ring

Part of: Forms and linear algebraic groups Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry Geometry of numbers Computational number theory Algebraic number theory: global fields

Published online by Cambridge University Press:  01 August 2014

Ilya Chevyrev  and
Steven D. Galbraith
Ilya Chevyrev
Affiliation:
Mathematical Institute, University of Oxford, United Kingdom email ilya.chevyrev@maths.ox.ac.uk
Steven D. Galbraith
Affiliation:
Mathematics Department, University of Auckland, New Zealand email S.Galbraith@math.auckland.ac.nz

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 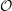$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathcal{O}$ be a maximal order in the quaternion algebra 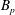$B_p$ over 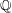$\mathbb{Q}$ ramified at 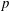$p$ and 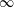$\infty $. The paper is about the computational problem: construct a supersingular elliptic curve 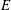$E$ over 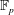$\mathbb{F}_p$ such that 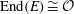${\rm End}(E) \cong \mathcal{O}$. We present an algorithm that solves this problem by taking gcds of the reductions modulo 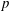$p$ of Hilbert class polynomials.

New theoretical results are required to determine the complexity of our algorithm. Our main result is that, under certain conditions on a rank three sublattice 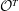$\mathcal{O}^T$ of 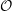$\mathcal{O}$, the order 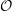$\mathcal{O}$ is effectively characterized by the three successive minima and two other short vectors of 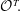$\mathcal{O}^T\! .$ The desired conditions turn out to hold whenever the 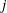$j$-invariant 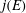$j(E)$, of the elliptic curve with 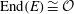${\rm End}(E) \cong \mathcal{O}$, lies in 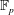$\mathbb{F}_p$. We can then prove that our algorithm terminates with running time 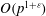$O(p^{1+\varepsilon })$ under the aforementioned conditions.

As a further application we present an algorithm to simultaneously match all maximal order types with their associated 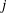$j$-invariants. Our algorithm has running time 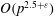$O(p^{2.5 + \varepsilon })$ operations and is more efficient than Cerviño’s algorithm for the same problem.

MSC classification

Secondary: 11G20: Curves over finite and local fields 11Y16: Algorithms; complexity 11R52: Quaternion and other division algebras 11E20: General ternary and quaternary quadratic forms; forms of more than two variables 11H55: Quadratic forms (reduction theory, extreme forms, etc.) 14G15: Finite ground fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 71 - 91
Copyright
© The Author(s) 2014 

References

Aho, A. V., Hopcroft, J. E. and Ullman, J. D., The design and analysis of computer algorithms (Addison-Wesley, Reading, MA, 1974).Google Scholar
Belding, J., Bröker, R., Enge, A. and Lauter, K., ‘Computing Hilbert class polynomials’, ANTS-VIII, Lecture Notes in Computer Science 5011 (eds van der Poorten, A. J. and Stein, A.; Springer, 2008) 282–295.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: the user language’, J. Symbolic Comput. 24 (1997) 235–265.CrossRefGoogle Scholar
Cerviño, J. M., ‘On the correspondence between supersingular elliptic curves and maximal quaternionic orders’, Mathematisches Institut Georg-August-Universität Göttingen Seminars Summer Term 2004 (Universitätsverlag Göttingen, 2004) 53–60.Google Scholar
Charles, D. X., Lauter, K. E. and Goren, E. Z., ‘Cryptographic hash functions from expander graphs’, J. Cryptology 22 (2009) no. 1, 93–113.Google Scholar
Cox, D. A., Primes of the form x 2 + n y 2 (Wiley, 1989).Google Scholar
Elkies, N., Ono, K. and Yang, T., ‘Reduction of CM elliptic curves and modular function congruences’, Int. Math. Res. Not. IMRN 44 (2005) 2695–2707.CrossRefGoogle Scholar
von zur Gathen, J. and Gerhard, J., Modern computer algebra (Cambridge University Press, 1999).Google Scholar
Goldwasser, S. and Micciancio, D., Complexity of lattice problems: a cryptographic perspective (Kluwer, 2002).Google Scholar
Henk, M., ‘Successive minima and lattice points’, Rend. Circ. Mat. Palermo (2) Suppl. (2002) 377–384.Google Scholar
Ibukiyama, T., ‘On maximal orders of division quaternion algebra over the rational number field with certain optimal embeddings’, Nagoya Math. J. 88 (1982) 181–195.CrossRefGoogle Scholar
Kane, B., ‘Representations of integers by ternary quadratic forms and CM liftings of supersingular elliptic curves’, PhD Thesis, University of Wisconsin-Madison, 2006.Google Scholar
Kaneko, M., ‘Supersingular j-invariants as singular moduli mod p’, Osaka J. Math. 26 (1989) 849–855.Google Scholar
Kohel, D., ‘Endomorphism rings of elliptic curves over finite fields’, PhD Thesis, University of California at Berkeley, 1996.Google Scholar
Pizer, A., ‘An algorithm for computing modular forms on Γ 0(N)’, J. Algebra 64 (1980) no. 2, 340–390.CrossRefGoogle Scholar
Schiemann, A., ‘Ternary positive definite quadratic forms are determined by their theta series’, Math. Ann. 308 (1997) 507–517.CrossRefGoogle Scholar
Siegel, C. L., Lectures on the geometry of numbers (Springer, 1989).CrossRefGoogle Scholar
Sutherland, A. V., ‘Computing Hilbert class polynomials using the Chinese remainder theorem’, Math. Comp. 80 (2011) 501–538.CrossRefGoogle Scholar
Sutherland, A. V., ‘On the evaluation of modular polynomials’, Algorithmic Number Theory 10th International Symposium (ANTS X), Open Book Series 1 (eds Howe, E. W. and Kedlaya, K. S.; Mathematical Sciences Publishers, 2013) 531–555.Google Scholar
Sutherland, A. V., ‘Isogeny volcanoes’, Algorithmic Number Theory 10th International Symposium (ANTS X), Open Book Series 1 (eds Howe, E. W. and Kedlaya, K. S.; Mathematical Sciences Publishers, 2013) 507–530.Google Scholar
Vignéras, M.-F., Arithmétique des algèbres de quaternions, Lecture Notes in Mathematics 800 (Springer, 1980).CrossRefGoogle Scholar
Yang, T., ‘Minimal CM liftings of supersingular elliptic curves’, Pure Appl. Math. Q. 4 (2008) no. 4, 1317–1326.CrossRefGoogle Scholar