Cuspidal quintics and surfaces with 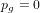$p_{g}=0$, 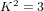$K^{2}=3$ and 5-torsion

Abstract

If $S$ is a quintic surface in 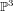$\mathbb{P}^{3}$ with singular set 15 3-divisible ordinary cusps, then there is a Galois triple cover 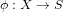${\it\phi}:X\rightarrow S$ branched only at the cusps such that 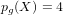$p_{g}(X)=4$, 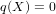$q(X)=0$, 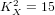$K_{X}^{2}=15$ and 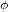${\it\phi}$ is the canonical map of 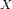$X$. We use computer algebra to search for such quintics having a free action of 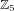$\mathbb{Z}_{5}$, so that 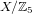$X/\mathbb{Z}_{5}$ is a smooth minimal surface of general type with 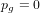$p_{g}=0$ and 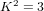$K^{2}=3$. We find two different quintics, one of which is the van der Geer–Zagier quintic; the other is new.

We also construct a quintic threefold passing through the 15 singular lines of the Igusa quartic, with 15 cuspidal lines there. By taking tangent hyperplane sections, we compute quintic surfaces with singular sets 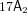$17\mathsf{A}_{2}$, 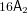$16\mathsf{A}_{2}$, 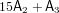$15\mathsf{A}_{2}+\mathsf{A}_{3}$ and 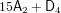$15\mathsf{A}_{2}+\mathsf{D}_{4}$.