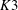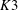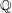Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Elsenhans, Andreas-Stephan
and
Jahnel, Jörg
2016.
Point counting on K3 surfaces and an application concerning real and complex multiplication.
LMS Journal of Computation and Mathematics,
Vol. 19,
Issue. A,
p.
12.
Elsenhans, Andreas-Stephan
and
Jahnel, Jörg
2020.
Mathematical Software – ICMS 2020.
Vol. 12097,
Issue. ,
p.
87.
Costa, Edgar
Elsenhans, Andreas-Stephan
and
Jahnel, Jörg
2020.
On the distribution of the Picard ranks of the reductions of a K3 surface.
Research in Number Theory,
Vol. 6,
Issue. 3,
Costa, Edgar
and
Sertöz, Emre Can
2021.
Arithmetic Geometry, Number Theory, and Computation.
p.
293.
Valloni, Domenico
2021.
Complex multiplication and Brauer groups of K3 surfaces.
Advances in Mathematics,
Vol. 385,
Issue. ,
p.
107772.
Heal, Kathryn
Kulkarni, Avinash
and
Sertöz, Emre Can
2022.
Deep Learning Gauss–Manin Connections.
Advances in Applied Clifford Algebras,
Vol. 32,
Issue. 2,
Elsenhans, Andreas-Stephan
and
Jahnel, Jörg
2023.
Explicit Families of K3 Surfaces Having Real Multiplication.
Michigan Mathematical Journal,
Vol. 73,
Issue. 1,
Elsenhans, Andreas-Stephan
and
Jahnel, Jörg
2024.
Real and Complex Multiplication on
K
3 Surfaces via Period Integration
.
Experimental Mathematics,
Vol. 33,
Issue. 2,
p.
193.
van Geemen, Bert
and
Schütt, Matthias
2025.
On families of K3 surfaces with real multiplication.
Forum of Mathematics, Sigma,
Vol. 13,
Issue. ,