Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alekseenko, E.
Aleshnikov, S.
Markin, N.
and
Zaytsev, A.
2011.
Optimal curves over finite fields with discriminant −19.
Finite Fields and Their Applications,
Vol. 17,
Issue. 4,
p.
350.
Lercier, Reynald
Ritzenthaler, Christophe
Rovetta, Florent
and
Sijsling, Jeroen
2014.
Parametrizing the moduli space of curves and applications to smooth plane quartics over finite fields.
LMS Journal of Computation and Mathematics,
Vol. 17,
Issue. A,
p.
128.
Gélin, Alexandre
Howe, Everett
and
Ritzenthaler, Christophe
2019.
Principally polarized squares of elliptic curves
with field of moduli equal to ℚ.
The Open Book Series,
Vol. 2,
Issue. 1,
p.
257.
Lercier, Reynald
Ritzenthaler, Christophe
Rovetta, Florent
Sijsling, Jeroen
and
Smith, Benjamin
2019.
Distributions of Traces of Frobenius for Smooth Plane Curves Over Finite Fields.
Experimental Mathematics,
Vol. 28,
Issue. 1,
p.
39.
Kirschmer, Markus
Narbonne, Fabien
Ritzenthaler, Christophe
and
Robert, Damien
2021.
Spanning the isogeny class of a power of an elliptic curve.
Mathematics of Computation,
Vol. 91,
Issue. 333,
p.
401.

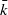 , being a Jacobian over
, being a Jacobian over 