Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T23:18:08.568Z Has data issue: false hasContentIssue false
  • English
  • Français

Finding 47:23 in the Baby Monster

Part of: Other groups of matrices Permutation groups

Published online by Cambridge University Press:  01 June 2016

John N. Bray ,
Richard A. Parker  and
Robert A. Wilson
John N. Bray
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, Mile End Road, London E1 4NS, United Kingdom email J.N.Bray@qmul.ac.uk
Richard A. Parker
Affiliation:
70 York Street, Cambridge CB1 2PY, United Kingdom email richpark54@hotmail.co.uk
Robert A. Wilson
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, Mile End Road, London E1 4NS, United Kingdom email R.A.Wilson@qmul.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we describe methods for finding very small maximal subgroups of very large groups, with particular application to the subgroup 47:23 of the Baby Monster. This example is completely intractable by standard or naïve methods. The example of finding 31:15 inside the Thompson group 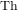$\text{Th}$ is also discussed as a test case.

MSC classification

Primary: 20B40: Computational methods
Secondary: 20H99: None of the above, but in this section
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 1 , 2016 , pp. 229 - 234
Copyright
© The Author(s) 2016 

References

Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language. Computational algebra and number theory (London, 1993)’, J. Symbolic Comput. 24 (1997) no. 3–4, 235–265.Google Scholar
Bray, J. N., ‘An improved method for generating the centralizer of an involution’, Arch. Math. (Basel) 74 (2000) 241–245.Google Scholar
Cannon, J. J. et al. , ‘The Magma programming language’. Various versions, 1994–present.Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., An atlas of finite groups (Clarendon Press, Oxford, 1985).Google Scholar
Holt, D. F., Eick, B. and O’Brien, E. A., Handbook of computational group theory. Discrete mathematics and its applications (Boca Raton) (Chapman & Hall/CRC, Boca Raton, FL, 2005).Google Scholar
Holmes, P. E., Linton, S. A., O’Brien, E. A., Ryba, A. J. E. and Wilson, R. A., ‘Constructive membership in black-box groups’, J. Group Theory 11 (2008) no. 6, 747–763.Google Scholar
Linton, S. A., ‘The art and science of computing in large groups’, Computational algebra and number theory (Sydney, 1992) , Mathematics and Its Applications 325 (Kluwer Academic Publishers, Dordrecht, 1995) 91–109.Google Scholar
Parker, R. A., ‘The computer calculation of modular characters (the MeatAxe)’, Computational group theory (Durham, 1982) (Academic Press, London, 1984) 267–274.Google Scholar
Ringe, M., ‘The C-MeatAxe programming language’, http://www.math.rwth-aachen.de/∼MTX/.Google Scholar
Wilson, R. A., ‘Some new subgroups of the Baby Monster’, Bull. Lond. Math. Soc. 25 (1993) no. 1, 23–28.Google Scholar
Wilson, R. A., Parker, R. A., Nickerson, S. J., Bray, J. N. et al. , ‘Atlas of finite group representations, version 3’ available at http://brauer.maths.qmul.ac.uk/Atlas/v3/.Google Scholar