Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T06:04:03.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Genus-2 curves and Jacobians with a given number of points

Part of: Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry Abelian varieties and schemes

Published online by Cambridge University Press:  01 February 2015

Reinier Bröker ,
Everett W. Howe ,
Kristin E. Lauter  and
Peter Stevenhagen
Reinier Bröker
Affiliation:
Department of Mathematics, Brown University, Box 1917, 151 Thayer Street, Providence, RI 02912, USA email reinier@math.brown.edu
Everett W. Howe
Affiliation:
Center for Communications Research, 4320 Westerra Court, San Diego, CA 92121, USA email however@alumni.caltech.edu
Kristin E. Lauter
Affiliation:
Microsoft Research, One Microsoft Way, Redmond, WA 98052, USA email klauter@microsoft.com
Peter Stevenhagen
Affiliation:
Mathematisch Instituut, Universiteit Leiden, Postbus 9512, 2300 RA Leiden, The Netherlands email psh@math.leidenuniv.nl

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the problem of efficiently constructing a curve 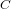$C$ of genus $2$ over a finite field $\mathbb{F}$ for which either the curve 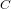$C$ itself or its Jacobian has a prescribed number 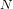$N$ of $\mathbb{F}$-rational points.

In the case of the Jacobian, we show that any ‘CM-construction’ to produce the required genus-$2$ curves necessarily takes time exponential in the size of its input.

On the other hand, we provide an algorithm for producing a genus-$2$ curve with a given number of points that, heuristically, takes polynomial time for most input values. We illustrate the practical applicability of this algorithm by constructing a genus-$2$ curve having exactly 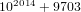$10^{2014}+9703$ (prime) points, and two genus-$2$ curves each having exactly 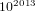$10^{2013}$ points.

In an appendix we provide a complete parametrization, over an arbitrary base field $k$ of characteristic neither two nor three, of the family of genus-$2$ curves over $k$ that have $k$-rational degree-$3$ maps to elliptic curves, including formulas for the genus-$2$ curves, the associated elliptic curves, and the degree-$3$ maps.

Supplementary materials are available with this article.

MSC classification

Primary: 14K22: Complex multiplication
Secondary: 11G15: Complex multiplication and moduli of abelian varieties 11G20: Curves over finite and local fields 14G15: Finite ground fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 170 - 197
Copyright
© The Author(s) 2015 

References

Baker, R. C., Harman, G. and Pintz, J., ‘The difference between consecutive primes. II’, Proc. Lond. Math. Soc. (3) 83 (2001) no. 3, 532–562; doi:10.1112/plms/83.3.532.Google Scholar
Bröker, R., ‘Constructing supersingular elliptic curves’, J. Comb. Number Theory 1 (2009) no. 3, 269–273.Google Scholar
Bröker, R. and Stevenhagen, P., ‘Efficient CM-constructions of elliptic curves over finite fields’, Math. Comp. 76 (2007) no. 260, 2161–2179; doi:10.1090/S0025-5718-07-01980-1.Google Scholar
Cohen, H., Diaz y Diaz, F. and Olivier, M., ‘Enumerating quartic dihedral extensions of ℚ’, Compositio Math. 133 (2002) no. 1, 65–93; doi:10.1023/A:1016310902973.Google Scholar
Eisenträger, K. and Lauter, K., ‘A CRT algorithm for constructing genus 2 curves over finite fields’, Arithmetics, geometry and coding theory (AGCT 2005) , Séminaires et Congrés 21 (eds Rodier, F. and Vlăduţ, S.; Société Mathématique de France, Paris, 2010) 161–176.Google Scholar
Fouquet, M. and Morain, F., ‘Isogeny volcanoes and the SEA algorithm’, Algorithmic number theory (Sydney, 2002) , Lecture Notes in Computer Science 2369 (eds Fieker, C. and Kohel, D. R.; Springer, Berlin, 2002) 276–291; doi:10.1007/3-540-45455-1_23.Google Scholar
Frey, G. and Kani, E., ‘Curves of genus 2 covering elliptic curves and an arithmetical application’, Arithmetic algebraic geometry (Texel, 1989) , Progress in Mathematics 89 (eds van der Geer, G., Oort, F. and Steenbrink, J. H. M.; Birkhäuser, Boston, 1991) 153–176; doi:10.1007/978-1-4612-0457-2_7.CrossRefGoogle Scholar
Goursat, E., ‘Sur la réduction des intégrales hyperelliptiques’, Bull. Soc. Math. France 13 (1885) 143–162; http://www.numdam.org/item?id=BSMF_1885__13__143_1.CrossRefGoogle Scholar
Hermite, Ch., ‘Sur un exemple de réduction d’intégrales abéliennes aux fonctions elliptiques’, Ann. Soc. Sci. Bruxelles Sér. I 1, 2nd part (1876) 1–16; http://books.google.com/books?id=gAvjAX4hTeYC.Google Scholar
Howe, E. W., Leprévost, F. and Poonen, B., ‘Large torsion subgroups of split Jacobians of curves of genus two or three’, Forum Math. 12 (2000) no. 3, 315–364; doi:10.1515/form.2000.008.CrossRefGoogle Scholar
Howe, E. W., Nart, E. and Ritzenthaler, C., ‘Jacobians in isogeny classes of abelian surfaces over finite fields’, Ann. Inst. Fourier (Grenoble) 59 (2009) no. 1, 239–289; doi:10.5802/aif.2430.CrossRefGoogle Scholar
Jacobi, C. G. J., ‘Review of Legendre’s Traité des fonctions elliptiques, troisième supplément ’, J. reine angew. Math. 8 (1832) 413–417; http://resolver.sub.uni-goettingen.de/purl?PPN243919689_0008.Google Scholar
Jacobi, C. G. J., Gesammelte Werke, Bände I–VIII (Chelsea, New York, 1969).Google Scholar
Kani, E., ‘The number of curves of genus two with elliptic differentials’, J. reine angew. Math. 485 (1997) 93–121; doi:10.1515/crll.1997.485.93.Google Scholar
Kohel, D. R., ‘Endomorphism rings of elliptic curves over finite fields’, PhD Thesis, University of California, Berkeley, 1996.Google Scholar
Kuhn, R. M., ‘Curves of genus 2 with split Jacobian’, Trans. Amer. Math. Soc. 307 (1988) no. 1, 41–49; doi:10.2307/2000749.CrossRefGoogle Scholar
Legendre, A. M., Traité des fonctions elliptiques et des intégrales Eulériennes, Tome troisième (Huzard–Courcier, Paris, 1828); http://gallica.bnf.fr/ark:/12148/bpt6k110149h.Google Scholar
Louboutin, S. R., ‘Lower bounds for relative class numbers of imaginary abelian number fields and CM-fields’, Acta Arith. 121 (2006) no. 3, 199–220; doi:10.4064/aa121-3-1.Google Scholar
Matomäki, K., ‘Large differences between consecutive primes’, Q. J. Math. 58 (2007) no. 4, 489–518; doi:10.1093/qmath/ham021.CrossRefGoogle Scholar
Mestre, J.-F., ‘Construction de courbes de genre 2 à partir de leurs modules’, Effective methods in algebraic geometry (Castiglioncello, 1990) , Progress in Mathematics 94 (eds Mora, T. and Traverso, C.; Birkhäuser, Boston, 1991) 313–334; doi:10.1007/978-1-4612-0441-1_21.CrossRefGoogle Scholar
Milne, J. S., ‘Jacobian varieties’, Arithmetic geometry (Storrs, Conn., 1984) (eds Cornell, G. and Silverman, J. H.; Springer, New York, 1986) 167–212; http://jmilne.org/math/articles/1986c.pdf.CrossRefGoogle Scholar
Shaska, T., ‘Genus 2 fields with degree 3 elliptic subfields’, Forum Math. 16 (2004) no. 2, 263–280; doi:10.1515/form.2004.013.CrossRefGoogle Scholar
Streng, M., ‘Computing Igusa class polynomials’, Math. Comp. 83 (2014) no. 285, 275–309; doi:10.1090/S0025-5718-2013-02712-3.Google Scholar
Sutherland, A. V., ‘Accelerating the CM method’, LMS J. Comput. Math. 15 (2012) 172–204; doi:10.1112/S1461157012001015.CrossRefGoogle Scholar
Tate, J., ‘Classes d’isogénie des variétés abéliennes sur un corps fini (d’après T. Honda)’, Séminaire Bourbaki, Vol. 1968/69: Exposés 347–363 , Lecture Notes in Mathematics 179 (Springer, Berlin, 1971) 95–110; doi:10.1007/BFb0058807.Google Scholar
Supplementary material: File

Bröker supplementary material

Bröker supplementary material 1

Download Bröker supplementary material(File)
File 16.8 KB