Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T05:57:03.888Z Has data issue: false hasContentIssue false
  • English
  • Français

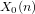Hyperelliptic modular curves $X_{0}(n)$ and isogenies of elliptic curves over quadratic fields

Part of: Number theory Arithmetic algebraic geometry

Published online by Cambridge University Press:  01 August 2015

Peter Bruin  and
Filip Najman
Peter Bruin
Affiliation:
Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL, United Kingdom email P.J.Bruin@math.leidenuniv.nl Current address:, Universiteit Leiden, Mathematisch Instituut, Postbus 9512, 2300 RA Leiden, The Netherlands
Filip Najman
Affiliation:
Department of Mathematics, University of Zagreb, Bijenička cesta 30, 10000 Zagreb, Croatia email fnajman@math.hr

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study elliptic curves over quadratic fields with isogenies of certain degrees. Let $n$ be a positive integer such that the modular curve 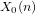$X_{0}(n)$ is hyperelliptic of genus 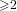${\geqslant}2$ and such that its Jacobian has rank $0$ over 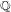$\mathbb{Q}$. We determine all points of 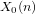$X_{0}(n)$ defined over quadratic fields, and we give a moduli interpretation of these points. 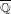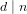We show that, with a finite number of exceptions up to $\overline{\mathbb{Q}}$-isomorphism, every elliptic curve over a quadratic field $K$ admitting an $n$-isogeny is $d$-isogenous, for some $d\mid n$, to the twist of its Galois conjugate by a quadratic extension $L$ of 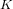$K$. We determine $d$ and $L$ explicitly, and we list all exceptions. As a consequence, again with a finite number of exceptions up to 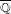$\overline{\mathbb{Q}}$-isomorphism, all elliptic curves with $n$-isogenies over quadratic fields are in fact 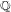$\mathbb{Q}$-curves.

MSC classification

Primary: 11G05: Elliptic curves over global fields 11G18: Arithmetic aspects of modular and Shimura varieties
Secondary: 11-04: Explicit machine computation and programs (not the theory of computation or programming)
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 578 - 602
Copyright
© The Author(s) 2015 

References

Bars, F., ‘Bielliptic modular curves’, J. Number Theory 76 (1999) 154–165.CrossRefGoogle Scholar
Bober, J., Deines, A., Klages-Mundt, A., LeVeque, B., Ohana, R. A., Rabindranath, A., Sharaba, P. and Stein, W., ‘A database of elliptic curves over ℚ(√5)—First Report’, Proceedings of the Tenth Algorithmic Number Theory Symposium (eds Howe, E. W. and Kedlaya, K. S.; Mathematical Sciences Publishers, Berkeley, CA, 2012) 145–166.Google Scholar
Bosma, W., Cannon, J. J., Fieker, C. and Steel, A. (eds), Handbook of magma functions , Edition 2.19 (2013).Google Scholar
Bosman, J. G., Bruin, P. J., Dujella, A. and Najman, F., ‘Ranks of elliptic curves with prescribed torsion over number fields’, Int. Math. Res. Not. IMRN 2014 (2014) 2885–2923.Google Scholar
Bruin, P. J. and Najman, F., ‘The growth of the rank of Abelian varieties upon extensions’, Ramanujan J. (2014); electronically published on 5 December.Google Scholar
Elkies, N. D., ‘Elliptic and modular curves over finite fields and related computational issues’, Computational perspectives on number theory (Chicago, IL, 1995) , AMS/IP Studies in Advanced Mathematics 7 (American Mathematical Society, Providence, RI, 1998) 21–76.Google Scholar
Galbraith, S. D., ‘Equations for modular curves’, DSc Thesis, University of Oxford, 1996.Google Scholar
Gonzàlez Rovira, J., ‘Equations of hyperelliptic modular curves’, Ann. Inst. Fourier 41 (1991) 779–795.Google Scholar
González, J., ‘Isogenies of polyquadratic ℚ-curves to their Galois conjugates’, Arch. Math. 77 (2001) 383–390.Google Scholar
Jeon, D., Kim, C. H. and Schweizer, A., ‘On the torsion of elliptic curves over cubic number fields’, Acta Arith. 113 (2004) 291–301.Google Scholar
Jeon, D., Kim, C. H. and Park, E., ‘On the torsion of elliptic curves over quartic number fields’, J. Lond. Math. Soc. (2) 74 (2006) 1–12.Google Scholar
Kamienny, S., ‘Torsion points on elliptic curves and q-coefficients of modular forms’, Invent. Math. 109 (1992) 221–229.Google Scholar
Katz, N. M., ‘ p-adic properties of modular schemes and modular forms’, Modular functions of one variable, III (Antwerp, 1972) , Lecture Notes in Mathematics 350 (Springer, Berlin, 1973) 69–190.Google Scholar
Kenku, M. A., ‘The modular curve X 0(39) and rational isogeny’, Math. Proc. Cambridge Philos. Soc. 85 (1979) 21–23.Google Scholar
Kenku, M. A., ‘The modular curves X 0(65) and X 0(91) and rational isogeny’, Math. Proc. Cambridge Philos. Soc. 87 (1980) 15–20.Google Scholar
Kenku, M. A., ‘The modular curve X 0(169) and rational isogeny’, J. Lond. Math. Soc. (2) 22 (1980) 239–244.Google Scholar
Kenku, M. A., ‘On the modular curves X 0(125), X 1(25) and X 1(49)’, J. Lond. Math. Soc. (2) 23 (1981) 415–427.Google Scholar
Kenku, M., ‘On the number of Q-isomorphism classes of elliptic curves in each Q-isogeny class’, J. Number Theory 15 (1982) 199–202.Google Scholar
Kenku, M. A. and Momose, F., ‘Torsion points on elliptic curves defined over quadratic fields’, Nagoya Math. J. 109 (1988) 125–149.Google Scholar
Mazur, B., ‘Modular curves and the Eisenstein ideal’, Publ. Math. Inst. Hautes Études Sci. 47 (1978) 33–186.Google Scholar
Mazur, B., ‘Rational isogenies of prime degree’, Invent. Math. 44 (1978) 129–162.Google Scholar
Merel, L., ‘Bornes pour la torsion des courbes elliptiques sur les corps de nombres’, Invent. Math. 124 (1996) 437–449.Google Scholar
Najman, F., ‘Torsion of rational elliptic curves over cubic fields and sporadic points on X 1(n)’, Math. Res. Lett. , to appear.Google Scholar
Ogg, A. P., ‘Hyperelliptic Modular Curves’, Bull. Soc. Math. France 102 (1974) 449–462.Google Scholar
Stein, W. A., ‘Explicit approaches to modular abelian varieties’, PhD Thesis, University of California, Berkeley, 2000.Google Scholar
Stoll, M., ‘Implementing 2-descent for Jacobians of hyperelliptic curves’, Acta Arith. 98 (2001) 245–277.Google Scholar
Vélu, J., ‘Isogénies entre courbes elliptiques’, C. R. Acad. Sci. Paris A 273 (1971) 238–241.Google Scholar