Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T15:46:02.917Z Has data issue: false hasContentIssue false
  • English
  • Français

JKL-ECM: an implementation of ECM using Hessian curves

Part of: Curves Arithmetic algebraic geometry Computational number theory

Published online by Cambridge University Press:  26 August 2016

Henriette Heer ,
Gary McGuire  and
Oisín Robinson
Henriette Heer
Affiliation:
Faculty of Mathematics, Technical University of Kaiserslautern, PO Box 3049, D-67653 Kaiserslautern, Germany email heer@rhrk.uni-kl.de
Gary McGuire
Affiliation:
School of Mathematics and Statistics, University College Dublin, Dublin 4, Ireland email gary.mcguire@ucd.ie
Oisín Robinson
Affiliation:
School of Mathematics and Statistics, University College Dublin, Dublin 4, Ireland email oisin.robinson@ucdconnect.ie

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present JKL-ECM, an implementation of the elliptic curve method of integer factorization which uses certain twisted Hessian curves in a family studied by Jeon, Kim and Lee. This implementation takes advantage of torsion subgroup injection for families of elliptic curves over a quartic number field, in addition to the ‘small parameter’ speedup. We produced thousands of curves with torsion 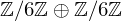$\mathbb{Z}/6\mathbb{Z}\oplus \mathbb{Z}/6\mathbb{Z}$ and small parameters in twisted Hessian form, which admit curve arithmetic that is ‘almost’ as fast as that of twisted Edwards form. This allows JKL-ECM to compete with GMP-ECM for finding large prime factors. Also, JKL-ECM, based on GMP, accepts integers of arbitrary size. We classify the torsion subgroups of Hessian curves over 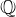$\mathbb{Q}$ and further examine torsion properties of the curves described by Jeon, Kim and Lee. In addition, the high-performance curves with torsion 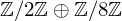$\mathbb{Z}/2\mathbb{Z}\oplus \mathbb{Z}/8\mathbb{Z}$ of Bernstein et al. are completely recovered by the 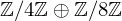$\mathbb{Z}/4\mathbb{Z}\oplus \mathbb{Z}/8\mathbb{Z}$ family of Jeon, Kim and Lee, and hundreds more curves are produced besides, all with small parameters and base points.

MSC classification

Primary: 11Y05: Factorization
Secondary: 11G05: Elliptic curves over global fields 14H52: Elliptic curves
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 83 - 99
Copyright
© The Author(s) 2016 

References

Bernstein, D. J., ‘Scaled remainder trees’, URL: http://cr.yp.to/papers.html#scaledmod. Note: draft, 2004.Google Scholar
Bernstein, D. J., ‘Fast multiplication and its applications’, Publ. Math. Inst. Hautes Études Sci. 44 (2008) 325–384.Google Scholar
Bernstein, D. J., ‘Explicit-formulas database’, 2016, http://www.hyperelliptic.org/EFD/.Google Scholar
Bernstein, D. J., Birkner, P., Joye, M., Lange, T. and Peters, C., ‘Twisted Edwards curves’, Progress in cryptology – AFRICACRYPT 2008 , Lecture Notes in Computer Science 5023 (Springer, Berlin, 2008) 389–405.Google Scholar
Bernstein, D. J., Birkner, P., Lange, T. and Peters, C., ‘ECM using Edwards curves’, Math. Comp. 82 (2013) 1139–1179.Google Scholar
Bernstein, D. J., Birkner, P., Lange, T. and Peters, C., ‘EECM-MPFQ’, 2016, http://eecm.cr.yp.to/mpfq.html.Google Scholar
Bernstein, D. J., Chuengsatiansup, C., Kohel, D. and Lange, T., ‘Twisted Hessian curves’, 2015,https://eprint.iacr.org/2015/781.pdf.Google Scholar
Bernstein, D. J. and Lange, T., ‘Analysis and optimization of elliptic-curve single-scalar multiplication’, Finite fields and applications , Contemporary Mathematics 461 (American Mathematical Society, Providence, RI, 2008) 1–19.Google Scholar
Brier, É. and Clavier, C., ‘New families of ECM curves for Cunningham numbers’, Algorithmic number theory: 9th international symposium, ANTS-IX , Lecture Notes in Computer Science 6197 (Springer, Berlin, 2010) 96–109.Google Scholar
Cox, D. A., Primes of the form x 2 + ny 2 , 2nd edn (John Wiley & Sons, Hoboken, NJ, 2013).Google Scholar
Dujella, A. and Najman, F., ‘Elliptic curves with large torsion and positive rank over number fields of small degree and ECM factorization’, Period. Math. Hungar. 65 (2012) 193–203.Google Scholar
Edwards, H. M., ‘A normal form for elliptic curves’, Bull. Amer. Math. Soc. (N.S.) 44 (2007) 393–422.Google Scholar
Hişil, H., Wong, K. K.-H., Carter, G. and Dawson, E., ‘Twisted Edwards curves revisited’, ASIACRYPT, 2008 , Lecture Notes in Computer Science 5350 (Springer, Berlin, Heidelberg, 2008).Google Scholar
Hişil, H., Wong, K. K.-H., Carter, G. and Dawson, E., ‘An exploration of affine group laws for elliptic curves’, J. Math. Cryptol. 5 (2011) 1–50.Google Scholar
Jeon, D., Kim, C. H. and Lee, Y., ‘Families of elliptic curves over quartic number fields with prescribed torsion subgroups’, Math. Comp. 80 (2011) 2395–2410.Google Scholar
Kenku, M. A. and Momose, F., ‘Torsion points on elliptic curves defined over quadratic fields’, Nagoya Math. J. 109 (1988) 125–149.CrossRefGoogle Scholar
Lenstra, H. W. Jr, ‘Factoring integers with elliptic curves’, Ann. of Math. (2) 126 (1987) 649–673.Google Scholar
Mazur, B., ‘Modular curves and the Eisenstein ideal’, Publ. Math. Inst. Hautes Études Sci. (1977) 33–186.Google Scholar
Montgomery, P. L., ‘An FFT extension of the elliptic curve method of factorization’, PhD Thesis, University of California, Los Angeles, ProQuest LLC, Ann Arbor, MI, 1992.Google Scholar
Schönhage, A. and Strassen, V., ‘Schnelle Multiplikation grosser Zahlen’, Computing (Arch. Elektron. Rechnen) 7 (1971) 281–292.Google Scholar
Zimmermann, P. et al. , ‘GMP-ECM’, 2016, http://ecm.gforge.inria.fr/.Google Scholar
Zimmermann, P. and Dodson, B., ‘20 years of ECM’, Algorithmic number theory: 7th international symposium, ANTS-VII , Lecture Notes in Computer Science 4076 (eds Hess, F., Pauli, S. and Pohst, M. E.; Springer, Berlin, 2006) 525–542.CrossRefGoogle Scholar