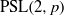Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Connor, Thomas
Jambor, Sebastian
and
Leemans, Dimitri
2015.
C-groups ofPSL(2,q)andPGL(2,q).
Journal of Algebra,
Vol. 427,
Issue. ,
p.
455.
Cameron, Peter
Lucchini, Andrea
and
Roney-Dougal, Colva
2018.
Generating sets of finite groups.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 9,
p.
6751.
Garzoni, Daniele
and
Lucchini, Andrea
2020.
Minimal invariable generating sets.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 1,
p.
218.
Cueto Noval, David
Lorenz, Aidan A.
and
Zadeoğlu, Baran
2021.
On the replacement property for PSL(2,
p
)
.
Communications in Algebra,
Vol. 49,
Issue. 11,
p.
4970.
Harper, Scott
2023.
The maximal size of a minimal generating set.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,