No CrossRef data available.
Article contents
A note on magnitude bounds for the mask coefficients of the interpolatory Dubuc–Deslauriers subdivision scheme
Published online by Cambridge University Press: 01 May 2014
Abstract
We analyse the mask associated with the 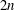 $2n$ -point interpolatory Dubuc–Deslauriers subdivision scheme
$2n$ -point interpolatory Dubuc–Deslauriers subdivision scheme 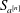 $S_{a^{[n]}}$ . Sharp bounds are presented for the magnitude of the coefficients
$S_{a^{[n]}}$ . Sharp bounds are presented for the magnitude of the coefficients 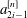 $a^{[n]}_{2i-1}$ of the mask. For scales
$a^{[n]}_{2i-1}$ of the mask. For scales 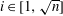 $i \in [1,\sqrt{n}]$ it is shown that
$i \in [1,\sqrt{n}]$ it is shown that 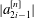 $|a^{[n]}_{2i-1}|$ is comparable to
$|a^{[n]}_{2i-1}|$ is comparable to 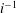 $i^{-1}$ , and for larger power scales, exponentially decaying bounds are obtained. Using our bounds, we may precisely analyse the summability of the mask as a function of
$i^{-1}$ , and for larger power scales, exponentially decaying bounds are obtained. Using our bounds, we may precisely analyse the summability of the mask as a function of  $n$ by identifying which coefficients of the mask contribute to the essential behaviour in
$n$ by identifying which coefficients of the mask contribute to the essential behaviour in  $n$ , recovering and refining the recent result of Deng–Hormann–Zhang that the operator norm of
$n$ , recovering and refining the recent result of Deng–Hormann–Zhang that the operator norm of 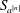 $S_{a^{[n]}}$ on
$S_{a^{[n]}}$ on 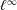 $\ell ^\infty $ grows logarithmically in
$\ell ^\infty $ grows logarithmically in  $n$ .
$n$ .
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014

