Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T06:45:39.308Z Has data issue: false hasContentIssue false
  • English
  • Français

On ${\it\lambda}$-invariants attached to cyclic cubic number fields

Part of: Zeta and $L$-functions: analytic theory Algebraic number theory: global fields

Published online by Cambridge University Press:  01 December 2015

Daniel Delbourgo  and
Qin Chao
Daniel Delbourgo
Affiliation:
Department of Mathematics, University of Waikato, Private Bag 3105, Hamilton, New Zealand email delbourg@waikato.ac.nz
Qin Chao
Affiliation:
Department of Mathematics, University of Waikato, Private Bag 3105, Hamilton, New Zealand email qinchao@me.com

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe an algorithm for finding the coefficients of 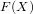$F(X)$ modulo powers of $p$, where 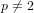$p\neq 2$ is a prime number and 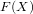$F(X)$ is the power series associated to the zeta function of Kubota and Leopoldt. We next calculate the 5-adic and 7-adic ${\it\lambda}$-invariants attached to those cubic extensions 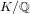$K/\mathbb{Q}$ with cyclic Galois group 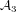${\mathcal{A}}_{3}$ (up to field discriminant 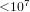${<}10^{7}$), and also tabulate the class number of 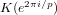$K(e^{2{\it\pi}i/p})$ for 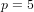$p=5$ and 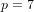$p=7$. If the ${\it\lambda}$-invariant is greater than zero, we then determine all the zeros for the corresponding branches of the $p$-adic $L$-function and deduce 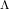${\rm\Lambda}$-monogeneity for the class group tower over the cyclotomic 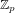$\mathbb{Z}_{p}$-extension of 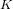$K$.

Supplementary materials are available with this article.

MSC classification

Primary: 11R23: Iwasawa theory
Secondary: 11M41: Other Dirichlet series and zeta functions 11R60: Cyclotomic function fields (class groups, Bernoulli objects, etc.)
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 684 - 698
Copyright
© The Author(s) 2015 

References

Childress, N. and Gold, R., ‘Zeros of p-adic L-functions’, Acta Arith. 48 (1987) 63–71.CrossRefGoogle Scholar
Delbourgo, D., ‘A Dirichlet series expansion for the p-adic zeta function’, J. Aust. Math. Soc. 81 (2006) 215–224.CrossRefGoogle Scholar
Delbourgo, D., ‘The convergence of Euler products over p-adic number fields’, Proc. Edinb. Math. Soc. 52 (2009) 583–606.Google Scholar
Ellenberg, J., Jain, S. and Venkatesh, A., ‘Modelling 𝜆-invariants by p-adic random matrices’, Commun. Pure Appl. Math. 64 (2011) 1243–1262.CrossRefGoogle Scholar
Ernvall, R. and MetsĂ€nkylĂ€, T., ‘A method for computing the Iwasawa 𝜆-invariant’, Math. Comp. 49 (1987) 281–294.Google Scholar
Ernvall, R. and MetsĂ€nkylĂ€, T., ‘Computation of the zeros of p-adic L-functions’, Math. Comp. 58 (1992) 815–830.Google Scholar
Ferrero, B. and Washington, L., ‘The Iwasawa 𝜇 p -invariant vanishes for abelian number fields’, Ann. of Math. (2) 109 (1979) 377–395.CrossRefGoogle Scholar
Greenberg, R., ‘A generalization of Kummer’s criterion’, Invent. Math. 21 (1973) 247–254.CrossRefGoogle Scholar
Kida, M., ‘Kummer’s criterion for totally real number fields’, Tokyo J. Math. 14 (1991) 309–317.Google Scholar
Kubota, T. and Leopoldt, H., ‘Eine p-adische Theorie der Zetawerte, I: EinfĂŒhrung der p-adischen Dirichletschen L-Funktionen’, J. reine angew. Math. 214 (1964) 328–339.Google Scholar
Llorente, P. and Quer, J., ‘On totally real cubic fields with discriminant D < 107 ’, Math. Comp. 50 (1988) 581–594.Google Scholar
MĂ€ki, S., The determination of units in real cyclic sextic fields , Lecture Notes in Mathematics 797 (Springer-Verlag, Berlin and New York, 1980).CrossRefGoogle Scholar
Mazur, B. and Wiles, A., ‘Class fields of abelian extensions of ℚ’, Invent. Math. 76 (1984) 179–330.Google Scholar
The PARI Group at Université de Bordeaux I, PARI/GP Version 2.7.0, 2014, available online from http://pari.math.u-bordeaux.fr/.Google Scholar
Roblot, X.-F., ‘Computing p-adic L-functions of totally real number fields’, Math. Comp. 84 (2015) 831–874.CrossRefGoogle Scholar
Wagstaff, S. Jr., ‘Zeros of p-adic L-functions’, Math. Comp. 29 (1975) 1138–1143.Google Scholar
Wagstaff, S. Jr., ‘Zeros of p-adic L-functions II’, Number theory related to Fermat’s last theorem (Cambridge, Mass. 1981) , Progress in Mathematics 26 (BirkhĂ€user, 1982) 297–308.CrossRefGoogle Scholar
Washington, L., Introduction to cyclotomic fields , 2nd edn, Graduate Texts in Mathematics 83 (Springer, 1997).CrossRefGoogle Scholar
Wiles, A., ‘The Iwasawa conjecture for totally real fields’, Ann. of Math. 131 (1990) no. 3, 493–540.CrossRefGoogle Scholar
Supplementary material: File

Delbourgo and Chao supplementary material

Delbourgo and Chao supplementary material 1

Download Delbourgo and Chao supplementary material(File)
File 439.3 KB