Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T11:26:23.908Z Has data issue: false hasContentIssue false
  • English
  • Français

On the characters of the Sylow $p$-subgroups of untwisted Chevalley groups 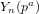$Y_{n}(p^{a})$

Part of: Representation theory of groups

Published online by Cambridge University Press:  01 October 2016

Frank Himstedt ,
Tung Le  and
Kay Magaard
Frank Himstedt
Affiliation:
Technische Universität München, Zentrum Mathematik – M11, Boltzmannstr. 3, 85748 Garching, Germany email himstedt@ma.tum.de
Tung Le
Affiliation:
North-West University, Mmabatho 2735, South Africa email lttung96@yahoo.com
Kay Magaard
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham B15 2TT, United Kingdom email k.magaard@bham.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

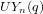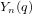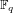Let $UY_{n}(q)$ be a Sylow $p$-subgroup of an untwisted Chevalley group $Y_{n}(q)$ of rank $n$ defined over $\mathbb{F}_{q}$ where $q$ is a power of a prime $p$. We partition the set 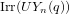$\text{Irr}(UY_{n}(q))$ of irreducible characters of 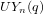$UY_{n}(q)$ into families indexed by antichains of positive roots of the root system of type 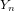$Y_{n}$. We focus our attention on the families of characters of 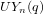$UY_{n}(q)$ which are indexed by antichains of length 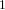$1$. Then for each positive root $\unicode[STIX]{x1D6FC}$ we establish a one-to-one correspondence between the minimal degree members of the family indexed by $\unicode[STIX]{x1D6FC}$ and the linear characters of a certain subquotient 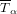$\overline{T}_{\unicode[STIX]{x1D6FC}}$ of 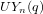$UY_{n}(q)$. For 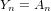$Y_{n}=A_{n}$ our single root character construction recovers, among other things, the elementary supercharacters of these groups. Most importantly, though, this paper lays the groundwork for our classification of the elements of 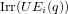$\text{Irr}(UE_{i}(q))$, 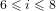$6\leqslant i\leqslant 8$, and 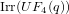$\text{Irr}(UF_{4}(q))$.

MSC classification

Primary: 20C15: Ordinary representations and characters 20C33: Representations of finite groups of Lie type
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 2 , 2016 , pp. 303 - 359
Copyright
© The Author(s) 2016 

References

André, C., ‘Basic characters of the unitriangular group (for arbitrary primes)’, Proc. Amer. Math. Soc. 130 (2002) 1943–1954.CrossRefGoogle Scholar
André, C. and Neto, A. M., ‘A supercharacter theory for the Sylow p-subgroups of the finite symplectic and orthogonal groups’, J. Algebra 322 (2009) 1273–1294.CrossRefGoogle Scholar
Borel, A. and Tits, J., ‘Groupes réductifs’, Publ. Math. Inst. Hautes Études Sci. 27 (1965) 55–150.Google Scholar
Carter, R. W., Simple groups of Lie type , Pure and Applied Mathematics 28 (John Wiley & Sons, London, 1972).Google Scholar
Cellini, P. and Papi, P., ‘Ad-nilpotent ideals of a Borel subalgebra. II’, J. Algebra 258 (2002) 112–121, special issue in celebration of Claudio Procesi’s 60th birthday.CrossRefGoogle Scholar
Diaconis, P. and Isaacs, I. M., ‘Supercharacters and superclasses for algebra groups’, Trans. Amer. Math. Soc. 360 (2008) 2359–2392.CrossRefGoogle Scholar
Digne, F. and Michel, J., Representations of finite groups of Lie type , London Mathematical Society Student Texts 21 (Cambridge University Press, Cambridge, 1991).Google Scholar
Djoković, D. Ž., ‘On conjugacy classes of elements of finite order in complex semisimple Lie groups’, J. Pure Appl. Algebra 35 (1985) 1–13.Google Scholar
Fomin, S. and Reading, N., ‘Root systems and generalized associahedra, Lecture notes for the IAS/Park City Graduate Summer School in Geometric Combinatorics’, Preprint, 2008, arXiv:0505518v3.Google Scholar
Geck, M., Hiss, G., Lübeck, F., Malle, G. and Pfeiffer, G., ‘CHEVIE—a system for computing and processing generic character tables’, Appl. Algebra Engrg. Comm. Comput. 7 (1996) 175–210.CrossRefGoogle Scholar
Goodwin, S. M., Le, T. and Magaard, K., ‘The generic character table of a Sylow $p$ -subgroup of a finite Chevalley group of type $D_{4}$ ’, Preprint, 2015, arXiv:1508.06937.Google Scholar
Goodwin, S. M., Le, T., Magaard, K. and Paolini, A., ‘Constructing characters of Sylow $p$ -subgroups of finite Chevalley groups’, Preprint, 2015, arXiv:1512.02678.CrossRefGoogle Scholar
Goodwin, S. M., Mosch, P. and Röhrle, G., ‘Calculating conjugacy classes in Sylow p-subgroups of finite Chevalley groups of rank six and seven’, LMS J. Comput. Math. 17 (2014) 109–122.Google Scholar
Goodwin, S. M., Mosch, P. and Röhrle, G., ‘On the coadjoint orbits of maximal unipotent subgroups of reductive groups’, Transform. Groups 21 (2016) 399–426.CrossRefGoogle Scholar
Goodwin, S. M. and Röhrle, G., ‘Calculating conjugacy classes in Sylow p-subgroups of finite Chevalley groups’, J. Algebra 321 (2009) 3321–3334.Google Scholar
Halasi, Z., ‘On representations of solvable linear groups’, PhD Thesis, Central European University, Budapest, 2009.Google Scholar
Halasi, Z. and Pálfy, P. P., ‘The number of conjugacy classes in pattern groups is not a polynomial function’, J. Group Theory 14 (2011) 841–854.Google Scholar
Higman, G., ‘Enumerating p-groups. I. Inequalities’, Proc. Lond. Math. Soc. (3) 10 (1960) 24–30.Google Scholar
Himstedt, F., ‘On the decomposition numbers of the Ree groups 2 F 4(q 2) in non-defining characteristic’, J. Algebra 325 (2011) 364–403.Google Scholar
Himstedt, F. and Huang, S.-C., ‘On the decomposition numbers of Steinberg’s triality groups 3 D 4(2 n ) in odd characteristics’, Comm. Algebra 41 (2013) 1484–1498.Google Scholar
Himstedt, F., Le, T. and Magaard, K., ‘Characters of the Sylow p-subgroups of the Chevalley groups D 4(p n )’, J. Algebra 332 (2011) 414–427.Google Scholar
Himstedt, F. and Noeske, F., ‘Decomposition numbers of SO7(q) and Sp6(q)’, J. Algebra 413 (2014) 15–40.Google Scholar
Humphreys, J. E., Introduction to Lie algebras and representation theory , Graduate Texts in Mathematics 9 (Springer, New York, 1997).Google Scholar
Huppert, B., Endliche Gruppen I , Die Grundlehren der Mathematischen Wissenschaften 134 (Springer, Berlin, 1967).CrossRefGoogle Scholar
Isaacs, I. M., Character theory of finite groups (Dover Publications, New York, 1994).Google Scholar
Isaacs, I. M., ‘Counting characters of upper triangular groups’, J. Algebra 315 (2007) 698–719.Google Scholar
Le, T., ‘Irreducible characters of the unitriangular groups’, PhD Thesis, Wayne State University, 2008.Google Scholar
Le, T. and Magaard, K., ‘On the character degrees of Sylow p-subgroups of Chevalley groups G (p f ) of type E ’, Forum Math. 27 (2015) 1–55.CrossRefGoogle Scholar
Marberg, E., ‘Heisenberg characters, unitriangular groups, and Fibonacci numbers’, J. Combin. Theory Ser. A 119 (2012) 882–903.CrossRefGoogle Scholar
Michel, J., ‘The development version of the CHEVIE package of GAP3’, Preprint, 2013,arXiv:1310.7905v2.Google Scholar
Okuyama, T. and Waki, K., ‘Decomposition numbers of Sp(4, q)’, J. Algebra 199 (1998) 544–555.CrossRefGoogle Scholar
Pak, I. and Soffer, A., ‘On Higman’s $k(U_{n}(\mathbb{F}_{q}))$ conjecture’, Preprint, 2015, arXiv:1507.00411.Google Scholar
Panyushev, D. I., ‘Ad-nilpotent ideals of a Borel subalgebra: generators and duality’, J. Algebra 274 (2004) 822–846.Google Scholar
Shi, J.-Y., ‘The number of ⊕-sign types’, Quart. J. Math. Oxford Ser. (2) 48 (1997) 93–105.Google Scholar
Sommers, E. N., ‘ B-stable ideals in the nilradical of a Borel subalgebra’, Canad. Math. Bull. 48 (2005) 460–472.Google Scholar
Vera-López, A. and Arregi, J. M., ‘Conjugacy classes in unitriangular matrices’, Linear Algebra Appl. 370 (2003) 85–124.CrossRefGoogle Scholar
Waki, K., ‘A note on decomposition numbers of G 2(2 n )’, J. Algebra 274 (2004) 602–606.Google Scholar