Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T22:21:01.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Václav Šimerka: quadratic forms and factorization

Part of: History of mathematics and mathematicians Computational number theory

Published online by Cambridge University Press:  01 May 2013

F. Lemmermeyer
F. Lemmermeyer*
Affiliation:
Mörikeweg 1,73489 Jagstzell,Germany email hb3@ix.urz.uni-heidelberg.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article we show that the Czech mathematician Václav Šimerka discovered the factorization of 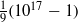$\frac{1}{9} (1{0}^{17} - 1)$ using a method based on the class group of binary quadratic forms more than 120 years before Shanks and Schnorr developed similar algorithms. Šimerka also gave the first examples of what later became known as Carmichael numbers.

MSC classification

Secondary: 11Y05: Factorization 01A55: 19th century
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 16 , October 2013 , pp. 118 - 129
Copyright
© The Author(s) 2013 

References

Arndt, F., ‘Ueber die Anzahl der Genera der quadratischen Formen’, J. Reine Angew. Math. 56 (1859) 72–78.Google Scholar
Bach, E., ‘Explicit bounds for primality testing and related problems’, Math. Comp. 55 (1990) 355–380.CrossRefGoogle Scholar
Bhargava, M., ‘Higher composition laws. I: a new view on Gauss composition, and quadratic generalizations’, Ann. of Math. (2) 159 (2004) 217–250.CrossRefGoogle Scholar
Carmichael, R. D., ‘On composite numbers $P$ which satisfy the Fermat congruence ${a}^{P- 1} \equiv 1~\mathrm{mod} ~P$ ’, Amer. Math. Monthly 19 (1912) 22–27.Google Scholar
Čupr, K., ‘Málo známé jubileum’, Časopis pro pěstování matematiky a fysiky 43 (1914) 482–489.CrossRefGoogle Scholar
Dickson, L., History of the theory of numbers, vol. I (1919) ; vol. II (1920); vol. III (1923) (Carnegie Institute of Washington); reprint (Chelsea, 1971).Google Scholar
Dirichlet, P. G. L., ‘Recherches sur diverses applications de l’analyse infinitésimale à la théorie des nombres’, J. Reine Angew. Math. 21 (1839) 1–12.Google Scholar
Ettingshausen, A. v., Die combinatorische Analysis als Vorbereitungslehre zum Studium der theoretischen höhern Mathematik (Vienna, 1825).Google Scholar
Flath, D., Introduction to number theory (Wiley & Sons, New York, 1989).Google Scholar
Hambleton, S. and Lemmermeyer, F., ‘Arithmetic of Pell surfaces’, Acta Arith. 146 (2011) 1–12.CrossRefGoogle Scholar
Hofmann, J. E., ‘Neues über Fermats zahlentheoretische Herausforderungen von 1657’, Abh. Preuss. Akad. Wiss. 9 (1943) 52.Google Scholar
Joubert, P., ‘Sur la théorie des fonctions elliptiques et son application à la théorie des nombres’, C.R. Acad. Sci. Paris 50 (1860) 774–779.Google Scholar
Kopáčkova, A., Počátky diferenciálního a integrálního počtu ve školské matematice, Proceedings of 10. setkání učitelú matematiky všech typú a stupnú škol (2006), 169–174.Google Scholar
Korselt, A., ‘Problème Chinois’, L’interméd. Math. 6 (1899) 142–143.Google Scholar
Lipschitz, R., ‘Einige Sätze aus der Theorie der quadratischen Formen’, J. Reine Angew. Math. 53 (1857) 238–259.Google Scholar
Pánek, A., ‘Život a pusobení p. Václava Šimerky’, Časopis pro pěstování matematiky a fysiky 17 (1888) 253–256.CrossRefGoogle Scholar
Scheffler, H., Die unbestimmte Analytik (Hannover, 1854).Google Scholar
Schnorr, C. P., ‘Refined analysis and improvements on some factoring algorithms’, J. Algorithms 3 (1982) 101–127.CrossRefGoogle Scholar
Schoof, R., ‘Quadratic fields and factorisation’, Computational methods in number theory (eds Tijdeman, R. and Lenstra, H.; Mathematisch Centrum, Amsterdam, 1982) 235–286, Tract 154.Google Scholar
Seysen, M., ‘A probabilistic factorization algorithm with quadratic forms of negative discriminant’, Math. Comp. 48 (1987) 757–780.CrossRefGoogle Scholar
Shanks, D., Class number, a theory of factorization and genera, Proceedings of Symposia in Pure Mathematics 20 (American Mathematical Society, 1971).CrossRefGoogle Scholar
Šimerka, W., ‘Die Perioden der quadratischen Zahlformen bei negativen Determinanten’, Sitzungsber. Kaiserl. Akad. Wiss., Math.-Nat.wiss. Classe 31 (1858) 33–67, presented May 14, 1858.Google Scholar
Šimerka, W., ‘Die trinären Zahlformen und Zahlwerthe’, Sitzungsber. Kaiserl. Akad. Wiss., Math.-Nat.wiss. Classe 38 (1859) 390–481.Google Scholar
Šimerka, W., ‘Lösung zweier Arten von Gleichungen’, Sitz.ber. Wien 33 (1859) 277–284.Google Scholar
Šimerka, W., Arch. Math. Phys. 51 (1866) 503–504.Google Scholar
Šimerka, V., ‘Poznámka (Number theoretic note)’, Casopis 8 (1879) 187–188.Google Scholar
Šimerka, V., ‘Zbytky z arithmetické posloupnosti (On the remainders of an arithmetic progression)’, Casopis 14 (1885) 221–225.Google Scholar
Sloane, N., ‘Online Encyclopedia of Integer Sequences’, A002997, http://oeis.org/A002997.Google Scholar
Wallis, J., Commercium epistolicum de quaestionibus mathematicis (Oxonium, 1658);http://reader.digitale-sammlungen.de/resolve/display/bsb10525798.html.Google Scholar