1. Introduction and Methods
A material at absolute zero is uniquely represented by the nature of its atoms, their spatial arrangement and the forces between them. In the rigid ion model it is assumed that the electron distribution is locked to the nuclei and is not affected by the lattice dynamics induced by increases in temperature and pressure. As one explores the state of matter at higher temperatures and pressures it is anticipated that most models will have increasing inaccuracies as interatomic interactions responsible for materials behavior are complex, generally non-linear, and are not well understood. Shell representations provide qualitative results for this difficult problem. First principle theories for calculating high temperature elastic constants have many approximations and assumptions and, as indicated earlier Reference Reeber and Wang[3] Reference Reeber and Wang[4], have difficulty in reproducing thermal expansion measurements over extended temperature ranges. Calculations of high temperature elastic constants Reference Gubanov and Davydov[5] based upon the central force model of Keating Reference Keating[6] Reference Keating[7] also have been questioned on theoretical grounds Reference Martin[8]. Most of the theoretical work provides zero K results for the temperature dependence of assumed quasi-harmonic cubic semiconductors.
It is well known that the thermophysical properties of crystal-chemically similar materials often can be simply correlated by corresponding states relationships Reference Blackman[9]. The symmetry of such materials provides a specific mathematical framework for describing the distribution of the fully excited 3N frequencies of a mole of atoms or molecules of a specific crystal structure. The stronger the material the higher is the temperature range that equivalent vibrational modes become excited. Simple correlations for melting, phase transitions and brittle to ductile transition temperatures have been made earlier Reference Reeber[10] Reference Reeber and Strens[11] Reference Reeber, Bradt, Evans, Hasselman and Lange[12].
In this work we use Debye temperatures as empirical corresponding states parameters to determine the elastic constants of SiC, AlN, GaN and InN from measured elastic constants of CdS Reference Gerlich[13]. It is assumed that:

Where:
for compounds A and B. Li and Bradt Reference Li and Bradt[14] have predicted the high temperature elastic constants for 6H α-silicon carbide. Their results are utilized as a test for our predictions.
2. Results
Table 1 lists the experimental literature values of the elastic constants for SiC, GaN, AlN and InN at room temperature. Elastic constants of SiC as measured by several authors Reference Arlt and Schodder[15] Reference Kamitani, Grimsditch, Nipko, Loong, Okada and Kimura[16] Reference Karmann, Helbig and Stein[17] are also given in Table 1. Table 2 provides our predictions for 6H-SiC. With the exception of a 13% difference for C13 the relative differences are significantly less than 7% with respect to Li and Bradt’s Reference Li and Bradt[14] results. The calculated Young’s modulus utilizing the Voigt-Ruess-Hill (VRH) average is within -2.3% at room temperature to +0.27% at 1250oK of Li and Bradt’s results. Table 3, 4 and 5 provide our predictions for AlN, GaN and InN. The room temperature elastic constant values necessary for our calculations are based upon literature results Reference Tsubouchi, Sugai and Mikoshiba[18] Reference McNeil, Grimsditch and French[19] Reference Deger, Born, Angerer, Ambacher, Stutzmann, Hornsteiner, Riha and Fischerauer[20] Reference Savastenko and Sheleg[21] Reference Polian, Grimsditch and Grzegory[22] Reference Takagi, Ahart, Azuhata, Sota, Suzuki and Nakamura[23] Reference Yamaguchi, Yagi, Azuhata, Sota, Suzuki, Chichibu and Nakamura[24] Reference Schwarz, Khachaturyan and Weber[25] Reference Deguchi, Ichiryu, Toshikawa, Sekiguchi, Sota, Matsuo, Azuhata, Yagi, Chichibu and Nakamura[26] Reference Yamaguchi, Yagi, Sota, Deguchi, Shimada and Nakamura[27] Reference Sheleg and Savastenk[28]. The Young’s moduli calculated from McNeil et al.’s data Reference McNeil, Grimsditch and French[19] for AlN are shown in Figure 1 with existing experimental data Reference Tsubouchi, Sugai and Mikoshiba[18] Reference McNeil, Grimsditch and French[19] Reference Deger, Born, Angerer, Ambacher, Stutzmann, Hornsteiner, Riha and Fischerauer[20] Reference Taylor and Lenie[29] Reference Lubis, Hecht and Graves[30] Reference Gerlich, Dole and Slack[31] Reference Boch, Glandus, Jarrige, Lecompte and Mexmain[32] Reference Ruh, Zangvil and Barlowe[33] Reference Kampfe, Eigenmann, Vöhringer and Löhe[34] Reference Carlotti, Fioretto, Giovannini, Palmieri, Socino, Verdini and Verona[35] Reference Shiosaki, Yamamoto, Oda, Harada and Kawabata[36]. For GaN, the room temperature elastic constants are based on the average of consistent measurements Reference Deger, Born, Angerer, Ambacher, Stutzmann, Hornsteiner, Riha and Fischerauer[20] Reference Polian, Grimsditch and Grzegory[22] Reference Yamaguchi, Yagi, Azuhata, Sota, Suzuki, Chichibu and Nakamura[24] Reference Deguchi, Ichiryu, Toshikawa, Sekiguchi, Sota, Matsuo, Azuhata, Yagi, Chichibu and Nakamura[26] Reference Yamaguchi, Yagi, Sota, Deguchi, Shimada and Nakamura[27]. For InN, theoretical values from Wright Reference Wright[37] are applied in our calculation. Although experimental data exists for InN, GaN results generated by the same authors are not consistent with others Reference Sheleg and Savastenk[28]. The temperature dependence of the Young’s moduli for other compounds investigated are provided in Figure 2.
Table 1 Room temperature elastic constants and Debye temperatures for SiC, AlN, GaN and InN.

Table 2 Elastic Properties of 6H-SiC
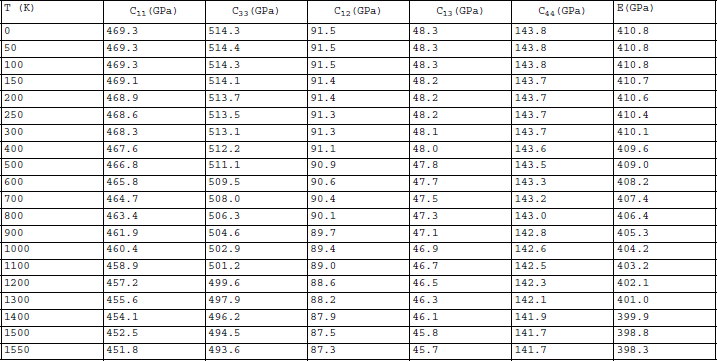
Table 3 Elastic Properties of AlN
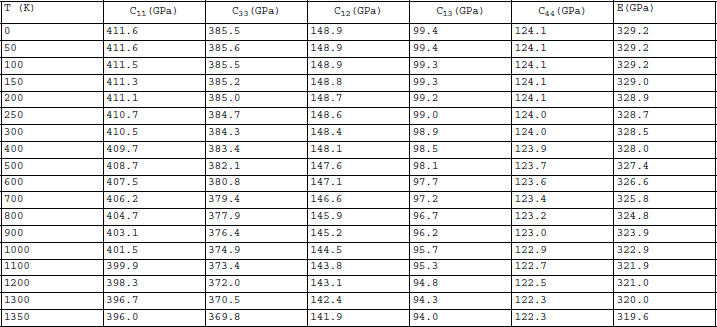
Table 4 Elastic Properties of GaN

Table 5 Elastic Properties of InN


Figure 1. Young’s Modulus of AlN

Figure 2. Temperature dependence of Young’s Modulus for AlN, GaN and InN.
3. Discussion and Conclusions
A complete set of the elastic constants for important semiconducting nitrides has been calculated over an extended temperature range by utilizing an empirical corresponding state relationship. Values shown for the experimentally measured Young’s moduli of AlN of Lubis et al. Reference Lubis, Hecht and Graves[30] and Ruh et al. Reference Ruh, Zangvil and Barlowe[33] are in reasonable agreement with our calculations. They had some porosity in their polycrystalline samples. At higher temperatures one might expect a brittle to ductile transition to occur. This would cause a reduction in the measured Young’s modulus. Unfortunately the mechanical property data available for comparison with our calculations is too limited to determine if such a transition occurs. In any case our results should be useful for estimating relative thermal residual stress variations under different growth conditions.
ACKNOWLEDGMENTS
The author appreciated the support of the Army Research Office through Grant No. DAAH04-93-D-0003. This work was carried out while one of the authors (K.W.) held a National Research Council-ARO Research Associateship.








