Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-11T06:57:03.354Z Has data issue: false hasContentIssue false
  • English
  • Français

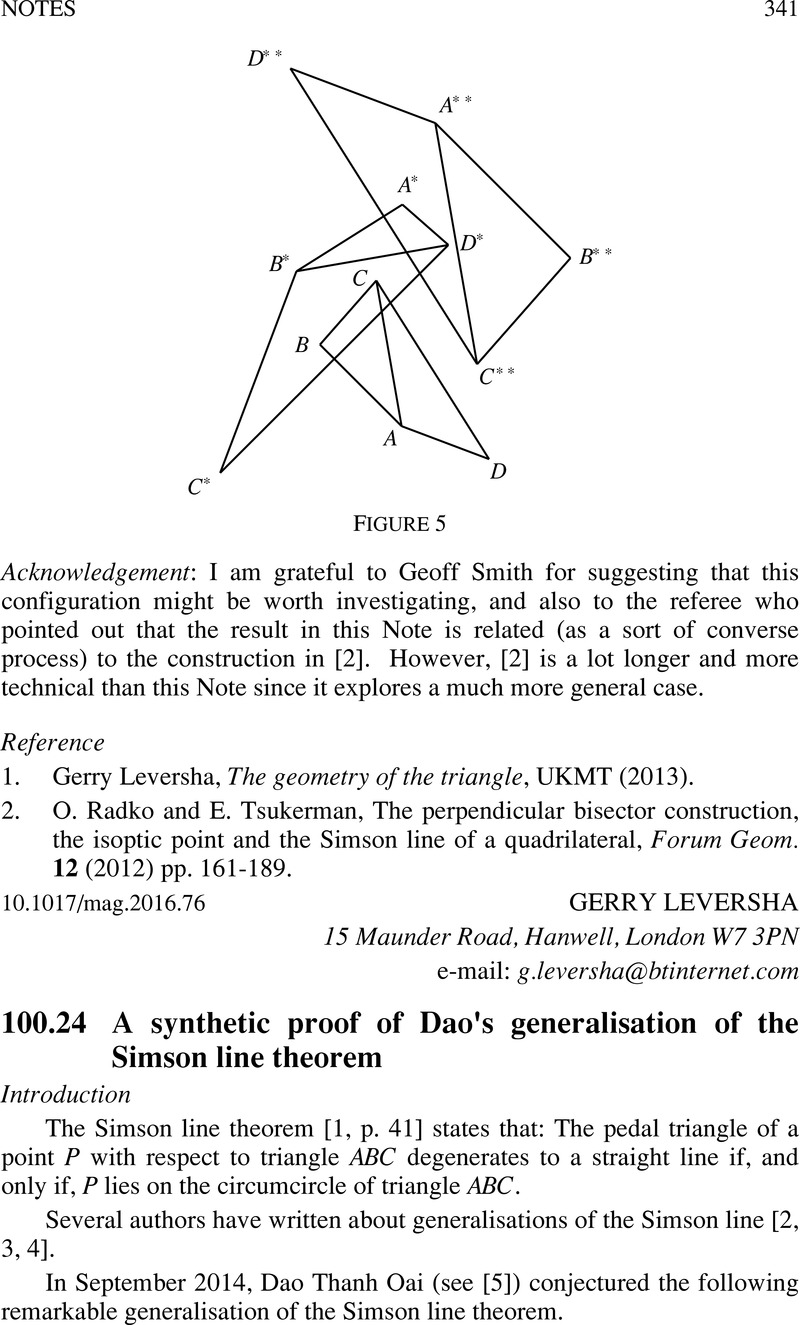
100.24 A synthetic proof of Dao's generalisation of the Simson line theorem

Published online by Cambridge University Press:  14 June 2016

Nguyen Le Phuoc  and
Nguyen Chuong Chi
Nguyen Le Phuoc
Affiliation:
501 CT7G, Duong Noi, Le Van Luong Stree, Ha Noi, Viet Nam e-mail: Nguyenlephuoc2006@gmail.com
Nguyen Chuong Chi
Affiliation:
Rowna 4 str., 05-075 Warsaw, Poland e-mail: Nguyenchuongchi@yahoo.com
Get access Rights & Permissions [Opens in a new window]

Abstract

An abstract is not available for this content so a preview has been provided. Please use the Get access link above for information on how to access this content.
Image of the first page of this content. For PDF version, please use the ‘Save PDF’ preceeding this image.'
Type
Notes
Information
The Mathematical Gazette , Volume 100 , Issue 548 , July 2016 , pp. 341 - 345
Copyright
Copyright © Mathematical Association 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Coxeter, H. S. M. and Greitzer, S.L., Geometry revisited, Math. Assoc. America, 1967.CrossRefGoogle Scholar
2.Bradley, C. J. and Bradley, J. T., Countless Simson line configurations, Math. Gaz., 80 (July 1996) pp. 314–321.CrossRefGoogle Scholar
3.Giering, O., Affine and projective generalization of Wallace lines, Journal for Geometry and Graphics 1 (1997), No. 2, pp. 119–133.Google Scholar
4.Pech, P., On the Simson-Wallace theorem and its generalizations, Journal for Geometry and Graphics, 9 (2005), No. 2, pp. 141–153.Google Scholar
5.Dao, T. O., Advanced plane geometry, message 1781, September 26, 2014, available at https://groups.yahoo.com/neo/groups/AdvancedPlaneGeometry/conversations/messages/1781Google Scholar
6.Bogomolny, A., A generalization of the Simson line, available at http://www.cut-the-knot.org/m/Geometry/GeneralizationSimson.shtmlGoogle Scholar