No CrossRef data available.
Article contents
Alice’s adventures in inverse tan land – mathematical argument, language and proof
Published online by Cambridge University Press: 21 October 2019
Extract
Andrew Palfreyman’s article [1] reminds us of the result(1)$${\rm{ta}}{{\rm{n}}^{{\rm{ - 1}}}}{\rm{+ta}}{{\rm{n}}^{{\rm{ - 1}}}}\,2{\rm{+ta}}{{\rm{n}}^{{\rm{ - 1}}}}{\rm{ 3= }}\,\pi {\rm{, }}$$having been set the challenge of finding the value of the left-hand side by his head of department at the start of a departmental meeting.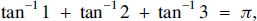
Information
- Type
- Articles
- Information
- Copyright
- © Mathematical Association 2019
References
Palfreyman, A., Inverse tan does it add up to anything?, Mathematics in School, 47(1) (2018) pp. 24-25.Google Scholar
Abeles, F. F., Charles, L. Dodgson’s geometric approach to arctangent relations for pi, Historia Mathematica, 20 (1993) pp. 151-159, also available at http://users.uoa.gr/~apgiannop/Sources/Dodgson-pi.pdf 10.1006/hmat.1993.1013CrossRefGoogle Scholar
Department for Education, GCE AS and A level subject content for mathematics (2014) also available at https://www.gov.uk/government/publications/gce-as-and-a-level-mathematicsGoogle Scholar

