Article contents
An alternative recursive formula for the sums of powers of integers
Published online by Cambridge University Press: 14 June 2016
Extract
The sums of powers of the first n positive integers Sp(n) = 1p + 2p + …+np, (p = 0, 1, 2, … )satisfy the fundamental identity
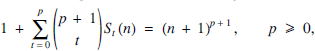 (1)
(1)
from which we can successively compute S0 (n), S1 (n), S2 (n), etc. Identity (1) can easily be proved by using the binomial theorem; see e.g. [1, 2]. Several variations of (1) are also well known [3, 4, 5].
In this note, we derive the following lesser-known recursive formula for Sp (n):
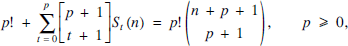 (2)
(2)
where 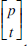 denote the (unsigned) Stirling numbers of the first kind, also known as the Stirling cycle numbers (see e.g. [6, Chapter 6]). Table 1 shows the first few rows of the Stirling number triangle. Although the recursive formula (2) is by no means new, our purpose in dealing with recurrence (2) in this note is two-fold. On one hand, we aim to provide a new algebraic proof of (2) by making use of two related identities involving the harmonic numbers.
denote the (unsigned) Stirling numbers of the first kind, also known as the Stirling cycle numbers (see e.g. [6, Chapter 6]). Table 1 shows the first few rows of the Stirling number triangle. Although the recursive formula (2) is by no means new, our purpose in dealing with recurrence (2) in this note is two-fold. On one hand, we aim to provide a new algebraic proof of (2) by making use of two related identities involving the harmonic numbers.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 2016
References
- 1
- Cited by

