Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-14T07:41:22.422Z Has data issue: false hasContentIssue false
  • English
  • Français

The Calculus as An Item in School Mathematics. (Continued from p. 246.)

Published online by Cambridge University Press:  03 November 2016

C. S. Jackson
Get access Rights & Permissions [Opens in a new window]

Extract

Passing very briefly here, but by no means very briefly in the classroom, over this treatment of velocity, a few words may be given to the problem of the tangent.

Type
Research Article
Information
The Mathematical Gazette , Volume 7 , Issue 111 , May 1914 , pp. 314 - 322
Copyright
Copyright © Mathematical Association 1914

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Time may be saved if some familiarity with the notion of a “rate” has been gained by arithmetical problems on wages per hour or per piece, railway fare per mile or per hour on different railway journeys,—and other simple statistical investigations.

* Abdank Abakanowicz, Les Intégraphes. A tracing point P, sliding on the tiller AP, which pivots on the fixed point A, is made to describe the curve

y = f(x),

the distance AM being constant, say unity.

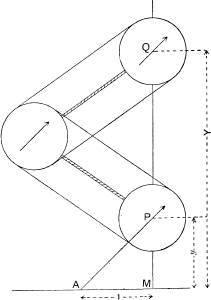
By various ingenious mechanical means, e.g. three equal pulleys with tightly stretched belts, a wheel Q is kept parallel to AP, and with its point of contact with the paper on MP produced. The wheel traces out on the paper a curve whose slope

* May yet one more digression in this discursive paper be permitted? Cannot the abominable phrase “moment of inertia” be stamped out? When applied, as it often is, to an area it is difficult to see a single argument in favour of its retention.

If “swing radius” or “radius of gyration,” with its perfectly definite physical meaning, is not acceptable as a substitute, cannot we agree to adopt the term “second moment about an axis” as an equivalent?

The mathematical analogy between the first and second moments for the case of n unit particles is illuminating, and the colourless character of the name renders its application to areas, volumes, weights and masses unobjectionable.

For n unit particles, and an axis Oy,

First moment M 1=n=x 1 + x 2+…+ x n.

Second moment M 2=nk 2=x 1 2 + x 2 2+…+x n 2.

(Note added, 1913.) I was very glad to hear from conversation in 1912 with Professor E. V Huntington that this is also his opinion.