Article contents
Cyclotomy and the heptadecagon
Published online by Cambridge University Press: 14 June 2016
Extract
Cyclotomy is concerned with the division of a circle into a given number of equal segments, amounting to the construction of a regular polygon, say a q-gon, so that we need to deliver the angle α = 2π / q, or the length cos α. The construction is by Euclidean means, which make use of only ruler and compasses. Now, from given lengths, sums and differences of lengths are easy to obtain and, with the compasses, products and quotients of lengths can be obtained from similar triangles using parallel lines; indeed even the length 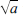 can be obtained by applying the intersecting chord theorem to a circle with diameter 1 + a. However, there is not much else one can do with the compasses, so that the length cos α has to come from the real roots of a sequence of quadratic equations with ‘suitable’ coefficients — the meaning of being suitable will be made clear later.
can be obtained by applying the intersecting chord theorem to a circle with diameter 1 + a. However, there is not much else one can do with the compasses, so that the length cos α has to come from the real roots of a sequence of quadratic equations with ‘suitable’ coefficients — the meaning of being suitable will be made clear later.
Gauss made the first significant contribution to the classical theory of cyclotomy in Article 365 of his famous Disquisitiones Arithmeticae [1] in 1801. He showed that the construction is possible if q = p is a Fermat prime, that is a prime of the form 22n + 1; see §7 for a necessary and sufficient condition for q. The only known Fermat primes are p = 3, 5, 17, 257, 65537; the cases p = 3, 5 and 17 correspond to the construction of the equilateral triangle, the regular pentagon, and the regular heptadecagon, the details for which Gauss gave.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 2016
References
- 1
- Cited by


