Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
2017.
Feedback.
The Mathematical Gazette,
Vol. 101,
Issue. 551,
p.
337.
Dolan, Stan
2018.
102.02 Minimal sets for congruence classes.
The Mathematical Gazette,
Vol. 102,
Issue. 553,
p.
93.

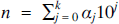 for some non-negative integer
for some non-negative integer 