Published online by Cambridge University Press: 23 January 2015
Many readers will be familiar with the sequence of Catalan numbers {Cn: n ≥ 0} and the formula

with its alternative form
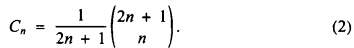
These can be proved by using recurrence relations, generating functions or André's reflection principle. A good reference for all of these methods is Martin Griffiths' book [1].
However, none of these approaches strikes me as being naturally combinatorial. A formula such as (1) is often derived by making a list of all the ways of doing something, and then subdividing this list into classes of equal size, so that either one class consists entirely of ‘valid’ cases or there is exactly one ‘valid’ case in each list.