Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-11T07:26:29.828Z Has data issue: false hasContentIssue false
  • English
  • Français

Euler, the clothoid and

Published online by Cambridge University Press:  14 June 2016

Nick Lord
Nick Lord*
Affiliation:
Tonbridge School, Kent TN9 1JP
Get access Rights & Permissions [Opens in a new window]

Extract

One of the many definite integrals that Euler was the first to evaluate was

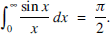(1)

He did this, almost as an afterthought, at the end of his short, seven-page paper catalogued as E675 in [1] and with the matter-of-fact title, On the values of integrals from x = 0 to x = ∞. It is a beautiful Euler miniature which neatly illustrates the unexpected twists and turns in the history of mathematics. For Euler's derivation of (1) emerges as the by-product of a solution to a problem in differential geometry concerning the clothoid curve which he had first encountered nearly forty years earlier in his paper E65, [1]. As highlighted in the recent Gazette article [2], E675 is notable for Euler's use of a complex number substitution to evaluate a real-variable integral. He used this technique in about a dozen of the papers written in the last decade of his life. The rationale for this manoeuvre caused much debate among later mathematicians such as Laplace and Poisson and the technique was only put on a secure footing by the work of Cauchy from 1814 onwards on the foundations of complex function theory, [3, Chapter 1]. Euler's justification was essentially pragmatic (in agreement with numerical evidence) and by what Dunham in [4, p. 68] characterises as his informal credo, ‘Follow the formulas, and they will lead to the truth.’ Smithies, [3, p. 187], contextualises Euler's approach by noting that, at that time, ‘a function was usually thought of as being defined by an analytic expression; by the principle of the generality of analysis, which was widely and often tacitly accepted, such an expression was expected to be valid for all values, real or complex, of the independent variable’. In this article, we examine E675 closely. We have tweaked notation and condensed the working in places to reflect modern usage. At the end, we outline what is, with hindsight, needed to make Euler's arguments watertight: it is worth noting that all of his conclusions survive intact and that the intermediate functions of one and two variables that he introduces in E675 remain the key ingredients for much subsequent work on these integrals.

Type
Research Article
Information
The Mathematical Gazette , Volume 100 , Issue 548 , July 2016 , pp. 266 - 273
Copyright
Copyright © Mathematical Association 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Mathematical Association of America, The Euler Archive, accessed March 2016 at http://eulerarchive.maa.org/Google Scholar
2.Glebov, G., A peculiar proof of an identity of Euler, Math. Gaz. 99 (March 2015) pp. 139–143.CrossRefGoogle Scholar
3.Smithies, F., Cauchy and the creation of complex function theory, Cambridge University Press (1997).CrossRefGoogle Scholar
4.Dunham, W., The calculus gallery, Princeton University Press (2005).CrossRefGoogle Scholar
5.Wolfram MathWorld, Cornu Spiral, accessed March 2016 at http://mathworld.wolfram.com/CornuSpiral.htmlGoogle Scholar
6.Archibald, R. C., Euler integrals and Euler's spiral, Amer. Math. Monthly 25 (1918) pp. 276–282.Google Scholar
7.Levien, R., The Euler spiral: a mathematical history, University of California, Berkeley (2008), available at: http://digitalassets.lib.berkeley.edu/techreports/ucb/text/EECS-2008-111.pdfGoogle Scholar
8.Bellos, A., Alex through the looking-glass, Bloomsbury (2014) pp. 226–231.Google Scholar
9.Jameson, G. J. O., Evaluating Fresnel-type integrals, Math. Gaz. 99 (November 2015) pp. 491–498.CrossRefGoogle Scholar
10.Nahin, P. J., Inside interesting integrals, Springer (2015).CrossRefGoogle Scholar
11.van Yzeren, J., Moivre's and Fresnel's integrals by simple integration, Amer. Math. Monthly 86 (1979) pp. 691–693.CrossRefGoogle Scholar
12.Chen, H., Excursions in classical analysis, Mathematical Association of America (2010) pp. 225–226.Google Scholar
13.Flanders, H., On the Fresnel integrals, Amer. Math. Monthly 89 (1982) pp. 264–266.Google Scholar
14.Loya, P., Dirichlet and Fresnel integrals via repeated integration, Mathematics Magazine 78 (2005) pp. 63–67.Google Scholar
15.Hardy, G. H., The integral , Math. Gaz. 5 (June-July 1909) pp. 98–103.CrossRefGoogle Scholar
16.Hardy, G. H., Further remarks on the integral , Math. Gaz. 8 (July 1916) pp. 301–303.CrossRefGoogle Scholar
17.Jameson, G. J. O., Sine, cosine and exponential integrals, Math. Gaz. 99 (July 2015) pp. 276–289.CrossRefGoogle Scholar
18.Körner, T. W., Exercises for Fourier analysis, Cambridge University Press (1993).CrossRefGoogle Scholar
19.Weir, A. J., Lebesgue integration and measure, Cambridge University Press (1973) pp. 118, 124.CrossRefGoogle Scholar
20.Euler, L. (translated by Bell, J.), On the values of integrals extended from the variable term x = 0 up to x = ∞, Cornell University Library (2008), available at http://arxiv.org/archive/math 0705.4640Google Scholar