Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T07:40:19.074Z Has data issue: false hasContentIssue false
  • English
  • Français

Fermat and the difference of two squares

Published online by Cambridge University Press:  23 January 2015

Stan Dolan
Stan Dolan*
Affiliation:
126A Harpenden Road, St. Albans, Herts AL3 6BZ
Get access Rights & Permissions [Opens in a new window]

Extract

In a previous note [1], Fermat's method of descente infinie was used to prove that the equations.

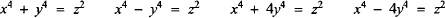
have no positive integer solutions. The geometrically based proof of [1] masked the underlying use of the difference of two squares. In the proofs of this article we shall make its use explicit, just as Fermat did [2, pp. 293-294].

We shall use the elementary idea of the difference of two squares to develop a powerful technique for solving equations of the form ax4 + bx2y2 + cy4 = z2. This will then be applied to three problems of historical interest.

Type
Articles
Information
The Mathematical Gazette , Volume 96 , Issue 537 , November 2012 , pp. 480 - 491
Copyright
Copyright © The Mathematical Association 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Dolan, S., Fermat's method of ‘descente infinie’, Math. Gaz. 95 (July 2011) pp. 269–271.Google Scholar
2. Heath, Sir T. L., Diophantus of Alexandria, Dover (1964).Google Scholar
3. Sigler, L. E., The Book of Squares, Academic Press (1987).Google Scholar
4. Ribenboim, P., Fermat's Last Theorem for Amateurs, Springer (1999).Google Scholar
5. Dolan, S., Pell's Equation and Fermat, Math. Gaz. 96 (March 2012), pp.99–102.Google Scholar
6. Washington, L. C., Elliptic Curves, Chapman & Hall/CRC (2003).Google Scholar