Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Al Rabee, Faeik T.
Al-Rimawi, Ashraf
and
Gitlin, Richard D.
2018.
Channel Capacity in a Dynamic Random Waypoint Mobility Model.
p.
711.
Abolhassani, Bahman
Tadrous, John
and
Eryilmaz, Atilla
2019.
Wireless Multicasting for Content Distribution: Stability and Delay Gain Analysis.
p.
1.
Smetana, Kathrin
Zahm, Olivier
and
Patera, Anthony T.
2019.
Randomized Residual-Based Error Estimators for Parametrized Equations.
SIAM Journal on Scientific Computing,
Vol. 41,
Issue. 2,
p.
A900.
Mayer, Alexander
2019.
Estimation and Inference in Adaptive Learning Models with Slowly Decreasing Gains.
SSRN Electronic Journal,
Eggers, Patrick C. F.
Angjelichinoski, Marko
and
Popovski, Petar
2019.
Wireless Channel Modeling Perspectives for Ultra-Reliable Communications.
IEEE Transactions on Wireless Communications,
Vol. 18,
Issue. 4,
p.
2229.
Atta, A. G.
Moatimid, G. M.
and
Youssri, Y. H.
2019.
Generalized Fibonacci Operational Collocation Approach for Fractional Initial Value Problems.
International Journal of Applied and Computational Mathematics,
Vol. 5,
Issue. 1,
Bai, Tong
Wang, Jingjing
Ren, Yong
and
Hanzo, Lajos
2019.
Energy-Efficient Computation Offloading for Secure UAV-Edge-Computing Systems.
IEEE Transactions on Vehicular Technology,
Vol. 68,
Issue. 6,
p.
6074.
Akkouchi, Mohamed
and
Ighachane, Mohamed Amine
2019.
Refinements of Some Recent Inequalities for Certain Special Functions.
Annales Mathematicae Silesianae,
Vol. 33,
Issue. 1,
p.
1.
Beghin, Luisa
and
Gajda, Janusz
2020.
Tempered Relaxation Equation and Related Generalized Stable Processes.
Fractional Calculus and Applied Analysis,
Vol. 23,
Issue. 5,
p.
1248.
Liu, Siqi
Melia, Adrian
Song, Xiaojing
and
Tippett, Mark
2020.
Singular diffusions, constant elasticity of variance processes and logarithmic rates of return.
The European Journal of Finance,
Vol. 26,
Issue. 9,
p.
837.
Mahata, Shantiram
and
Sinha, Rajen Kumar
2020.
On the existence, uniqueness and stability results for time-fractional parabolic integrodifferential equations.
Journal of Integral Equations and Applications,
Vol. 32,
Issue. 4,
Tarable, Alberto
and
Escribano, Francisco J.
2020.
Chaos-Based Anytime-Reliable Coded Communications.
IEEE Systems Journal,
Vol. 14,
Issue. 2,
p.
2214.
Chavez, Gordon V.
2020.
Dynamic tail inference with log-Laplace volatility.
Extremes,
Vol. 23,
Issue. 2,
p.
287.
Kakavas-Papaniaros, P. A.
2020.
On the distribution of particles in propellant solids.
Acta Mechanica,
Vol. 231,
Issue. 3,
p.
863.
Mathias, Simon A.
Dentz, Marco
and
Liu, Qingquan
2020.
Gas Diffusion in Coal Powders is a Multi-rate Process.
Transport in Porous Media,
Vol. 131,
Issue. 3,
p.
1037.
Adjabi, Yassine
Samei, Mohammad Esmael
Matar, Mohammed M.
and
Alzabut, Jehad
2021.
Langevin differential equation in frame of ordinary and Hadamard fractional derivatives under three point boundary conditions.
AIMS Mathematics,
Vol. 6,
Issue. 3,
p.
2796.
Morales, Guillermo B.
and
Muñoz, Miguel A.
2021.
Immune amnesia induced by measles and its effects on concurrent epidemics.
Journal of The Royal Society Interface,
Vol. 18,
Issue. 179,
p.
20210153.
Linares Cedeño, Francisco X.
and
Nucamendi, Ulises
2021.
Revisiting cosmological diffusion models in Unimodular Gravity and the H0 tension.
Physics of the Dark Universe,
Vol. 32,
Issue. ,
p.
100807.
Beghin, Luisa
and
Ricciuti, Costantino
2021.
Lévy Processes Linked to the Lower-Incomplete Gamma Function.
Fractal and Fractional,
Vol. 5,
Issue. 3,
p.
72.
Budde, Christian
2021.
Positive Desch-Schappacher perturbations of bi-continuous semigroups on AM-spaces.
Acta Scientiarum Mathematicarum,
Vol. 87,
Issue. 3-4,
p.
571.
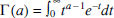 for a > 0. By splitting this integral at a point x ⩾ 0, we obtain the two incomplete gamma functions:
for a > 0. By splitting this integral at a point x ⩾ 0, we obtain the two incomplete gamma functions: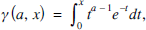 (1)
(1)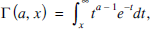 (2)
(2)
