On the Connection between the Inscribed and Escribed Circles of a Triangle

Extract

The chief object of this paper is to investigate a method of obtaining from any proposition connected with the inscribed circle of a plane triangle a corresponding proposition connected with one of the escribed circles of a plane triangle.

If we let a, b, c represent three lengths and A, B, C three angles, with the following limitations:

I. All six quantities must be positive,

II. A + B + C = π,

III.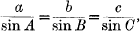

we can regard a, b, c, A, B, C as the sides and angles of a plane triangle, and then by the methods of Algebra and Trigonometry we can deduce a number of algebraical and trigonometrical relations connecting them.