Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-11T08:17:53.339Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Inversion Property of the Mobius’ μ-Function

Published online by Cambridge University Press:  03 November 2016

U. V. Satyanarayana
U. V. Satyanarayana*
Affiliation:
Dept. of Maths., Andhra University, Waltair, South India
Get access Rights & Permissions [Opens in a new window]

Extract

Mobius‘ function has the important property of inverting functional relations [1] of the type and 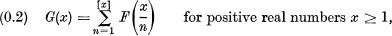giving in turn 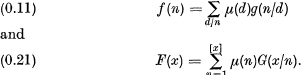(Also relations (0.1) and (0.2) follow respectively from (0.11) and (0.21))

I establish in this paper that no other arithmetical function μ*(n) can perform the above inversion. In other words, I prove that Inversion is the characteristic property of Mobius‘ μ-function. Theorem 1 below asserts that if for one pair of functions g(n) and f(n) (subject to a special condition) relations (0.1) and (0.11) are true with an arithmetical function μ*(n) (possibly depending on g and f), then μ*(n) coincides with the Mobius‘-function. Theorem 2 below gives a similar result in connection with functions G(x) and F(x) defined for all real x ≥ 1.

Type
Research Article
Information
The Mathematical Gazette , Volume 47 , Issue 359 , February 1963 , pp. 38 - 42
Copyright
Copyright © Mathematical Association 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Hardy, G. H. and Wright, E. M.: An Introduction To The Theory Of Numbers (Oxford University Press, 1945), pp. 235–236.Google Scholar
[2] Swetharanyam, S.: “A note on the Mobius function” The Math. Gazette, Vol. XLV, No. 351, February 1961, pp. 43–47.Google Scholar