A poor person's approximation to π

Extract

Suppose that we have a computing machine that can only deal with the operations of addition, subtraction and multiplication, but not division, of integers. Can such a machine be used to find the decimal expansion of a given real number α to an arbitrary length? The answer is ‘yes’, at least in the sense that α is the limit of a sequence of rational numbers, and one can obtain the decimal expansion of a positive rational number a/b without division. For example, for any positive k, we try all non-negative c < b and d < 10^ka, and see if 10^ka = db + c. There will be success because all we are doing is reducing 10^ka modulo b in a particularly moronic way. This guarantees the existence and uniqueness of d, and d/10^k is then the desired expansion. Take, for example, 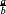= 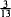and k = 12; then, after a tedious search, we should find that, for c = 3, there is d = 230 769 230 769 because 3 × 10¹² = 230769230769 × 13 + 3, so that 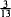= 0.230769230769 + 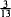× 10^-12. Such a procedure of searching for c, d is hopelessly inefficient, of course, and a more efficient method is given in the next section.