Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T07:26:13.130Z Has data issue: false hasContentIssue false
  • English
  • Français

Stop-sign theorems and binomial coefficients*

Published online by Cambridge University Press:  23 January 2015

Peter Hilton  and
Jean Pedersen
Peter Hilton
Affiliation:
Mathematical Sciences Department, SUNY at Binghamton, Binghamton, NY 13902-6000 USA
Jean Pedersen
Affiliation:
Department of Mathematics & CS, Santa Clara University, Santa Clara, CA 95053-0290 USA, e-mail:jpedersen@scu.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Dedicated to the memory of Russell Towle, a remarkable man who contributed so much to geometry and to other aspects of the quality of life.

We introduce an expanded notation 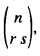where r + s = n, for the binomial coefficient 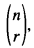, and then use this expanded notation to develop theorems involving 8 binomial coefficients, analogous to the Star of David Theorem, which. in its original form, involved the 6 neighbours of a given binomial coefficient in the Pascal Triangle (see Section 3), that appeared in [1,2,3,4,5,6,7,8,9].

Type
Articles
Information
The Mathematical Gazette , Volume 94 , Issue 530 , July 2010 , pp. 247 - 261
Copyright
Copyright © The Mathematical Association 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

The material in this article was presented by the second author at the eighth Gathering for Gardner Conference (G4G8), in Atlanta, GA on 29 March 2008.

References

1. Gould, H. W., Equal products of generalized binomial coefficients, Fibonacci Quarterly 9 (1971) pp. 337–346.Google Scholar
2. Hilton, Peter, Holton, Derek and Pedersen, Jean, Mathematical reflections-in a room with many mirrors, Springer Verlag, N.Y. (1998) pp. 211–216.Google Scholar
3. Hilton, Peter, Holton, Derek, and Pedersen, Jean, Mathematical vistas-from a room with many windows, Springer Verlag, N. Y. (2002) pp. 172–193.Google Scholar
4. Hoggatt, V. E. Jr, and Alexanderson, G. L., A property of multinomial coefficients, Fibonacci Quarterly 9 (1971) pp. 351-356, 420.Google Scholar
5. Hoggatt, V. E., and Hansell, W., The hidden hexagon squares, Fibonacci Quarterly 9 (1971) p. 120.Google Scholar
6. Long, Calvin T., Arrays of binomial coefficients whose products are squares, Fibonacci Quarterly, 11 (1973) pp. 449–456.Google Scholar
7. Long, Calvin T. and Hoggatt, Verner E. Jr. Sets of Binomial coefficients with equal products, Fibonacci Quarterly 12 (1974) pp.71–79.Google Scholar
8. Long, Calvin T. and Ando, Shiro, Another generalization of Gould's Star of David Theorem, Fibonacci Quarterly 30 (1992) pp. 251–255.Google Scholar
9. Usiskin, Zalman, Perfect square patterns in the Pascal triangle, Math. Mag. 46 (1973) pp. [203–208.Google Scholar